第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 教材P84习题T1·变式 若等腰三角形有一个内角为$110^{\circ }$,则这个等腰三角形的底角是(
A.$70^{\circ }$
B.$45^{\circ }$
C.$35^{\circ }$
D.$50^{\circ }$
C
).A.$70^{\circ }$
B.$45^{\circ }$
C.$35^{\circ }$
D.$50^{\circ }$
答案:
C
2. (2024·兰州中考)如图,在$△ABC$中,$AB= AC,$$∠BAC= 130^{\circ },DA⊥AC$,则$∠ADB= ($

A.$100^{\circ }$
B.$115^{\circ }$
C.$130^{\circ }$
D.$145^{\circ }$
B
$).$
A.$100^{\circ }$
B.$115^{\circ }$
C.$130^{\circ }$
D.$145^{\circ }$
答案:
B [解析]在△ABC中,AB=AC,
∴∠B=∠C.
∵∠BAC=130°,
∴∠B=∠C=$\frac{180° - 130°}{2}$=25°.
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90° - 25°=65°,
∴∠ADB=180° - ∠ADC=180° - 65°=115°.
故选B
思路引导 解答本题需要先根据等边对等角得出∠B=∠C,再根据∠BAC=130°即可求出∠C的度数,由DA⊥AC得出∠DAC=90°,从而求出∠ADC的度数.
∴∠B=∠C.
∵∠BAC=130°,
∴∠B=∠C=$\frac{180° - 130°}{2}$=25°.
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90° - 25°=65°,
∴∠ADB=180° - ∠ADC=180° - 65°=115°.
故选B
思路引导 解答本题需要先根据等边对等角得出∠B=∠C,再根据∠BAC=130°即可求出∠C的度数,由DA⊥AC得出∠DAC=90°,从而求出∠ADC的度数.
3. 实验班原创 如果等腰三角形的一个内角为另一个内角的2倍,那么该等腰三角形的底角等于(
A.$36^{\circ }$
B.$45^{\circ }$
C.$36^{\circ }或45^{\circ }$
D.$45^{\circ }或72^{\circ }$
D
).A.$36^{\circ }$
B.$45^{\circ }$
C.$36^{\circ }或45^{\circ }$
D.$45^{\circ }或72^{\circ }$
答案:
D
4. (2024·湖南中考)若等腰三角形的一个底角的度数为$40^{\circ }$,则它的顶角的度数为
100
°.
答案:
100 [解析]
∵等腰三角形的一个底角的度数为40°,
∴这个等腰三角形的另一个底角的度数为40°,
∴等腰三角形的顶角的度数为180° - 2×40°=100°.
∵等腰三角形的一个底角的度数为40°,
∴这个等腰三角形的另一个底角的度数为40°,
∴等腰三角形的顶角的度数为180° - 2×40°=100°.
5. 分类讨论思想 (2024·镇江中考)等腰三角形的两边长分别为6和2,则第三边长为____
6
.
答案:
6 [解析]当6为一腰长时,则另一腰长为6,底边长为2,
∵6 + 6>2,
∴能构成三角形,
∴第三边长为6;
当2为一腰长时,则另一腰长为2,底边长为6,
∵2 + 2<6,
∴不能构成三角形,舍去
切勿忽略三角形三边关系
综上,第三边长为6.
归纳总结 分两种情况讨论:当6为一腰长时;当2为一腰长时,分别求出第三条边长,并根据三角形三边关系判断是否能构成三角形,即可得出答案.
∵6 + 6>2,
∴能构成三角形,
∴第三边长为6;
当2为一腰长时,则另一腰长为2,底边长为6,
∵2 + 2<6,
∴不能构成三角形,舍去
切勿忽略三角形三边关系
综上,第三边长为6.
归纳总结 分两种情况讨论:当6为一腰长时;当2为一腰长时,分别求出第三条边长,并根据三角形三边关系判断是否能构成三角形,即可得出答案.
6. (2024·绥化中考)如图,$AB// CD,∠C= 33^{\circ },$$OC= OE$,则$∠A= $
66
°.
答案:
66 [解析]
∵OC=OE,∠C=33°,
∴∠E=∠C=33°,
∴∠DOE=∠E + ∠C=66°.
∵AB//CD,
∴∠A=∠DOE=66°.
∵OC=OE,∠C=33°,
∴∠E=∠C=33°,
∴∠DOE=∠E + ∠C=66°.
∵AB//CD,
∴∠A=∠DOE=66°.
7. 中考新考法 尺规作图 如图,在$△ABC$中,$∠C= $$90^{\circ },BC= 5.$
(1)利用直尺和圆规在AB边上求作一点P,使得$∠APC+∠BCP= 90^{\circ }$;(不写作法,保留作图痕迹)
(2)在(1)的条件下,试判断$∠PCB与∠A$之间的数量关系,并说明理由.

(1)利用直尺和圆规在AB边上求作一点P,使得$∠APC+∠BCP= 90^{\circ }$;(不写作法,保留作图痕迹)
(2)在(1)的条件下,试判断$∠PCB与∠A$之间的数量关系,并说明理由.

答案:
(1)如图,点P即为所求

(2)∠PCB=$\frac{1}{2}$∠A.理由如下:
由作图可知,AC=AP,∠ACP=∠APC,
∴∠A + 2∠ACP=180°,
∴$\frac{1}{2}$∠A + ∠ACP=90°.
∵∠ACB=90°,
∴∠PCB + ∠ACP=90°,
∴∠PCB=$\frac{1}{2}$∠A.
(1)如图,点P即为所求

(2)∠PCB=$\frac{1}{2}$∠A.理由如下:
由作图可知,AC=AP,∠ACP=∠APC,
∴∠A + 2∠ACP=180°,
∴$\frac{1}{2}$∠A + ∠ACP=90°.
∵∠ACB=90°,
∴∠PCB + ∠ACP=90°,
∴∠PCB=$\frac{1}{2}$∠A.
8. (2025·河北石家庄新乐期末)如图,在$△ABC$中,$AB= AC,AD,BE分别是△ABC$的中线和角平分线.若$∠CAD= 20^{\circ }$,则$∠ABE$的度数为(

A.$20^{\circ }$
B.$35^{\circ }$
C.$40^{\circ }$
D.$70^{\circ }$
B
).
A.$20^{\circ }$
B.$35^{\circ }$
C.$40^{\circ }$
D.$70^{\circ }$
答案:
B [解析]
∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,
∴∠ABC=∠C=$\frac{1}{2}$(180° - ∠CAB)=70°.
∵BE是△ABC的角平分线,
∴∠ABE=$\frac{1}{2}$∠ABC=35°.故选B.
∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,
∴∠ABC=∠C=$\frac{1}{2}$(180° - ∠CAB)=70°.
∵BE是△ABC的角平分线,
∴∠ABE=$\frac{1}{2}$∠ABC=35°.故选B.
9. 如图,D,E分别是$△ABC$的边BC,AC上的点,若$AB= AC,AD= AE$,则(
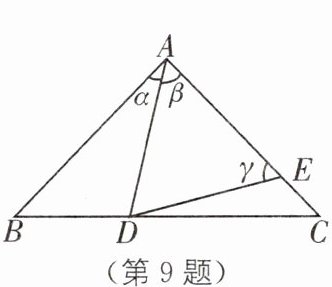
A.当$∠B$为定值时,$∠CDE$为定值
B.当α为定值时,$∠CDE$为定值
C.当β为定值时,$∠CDE$为定值
D.当γ为定值时,$∠CDE$为定值
B
).
A.当$∠B$为定值时,$∠CDE$为定值
B.当α为定值时,$∠CDE$为定值
C.当β为定值时,$∠CDE$为定值
D.当γ为定值时,$∠CDE$为定值
答案:
B
查看更多完整答案,请扫码查看


