《2025年实验班提优训练八年级数学上册人教版》

例1 (2025·广东韶关期中)下列长度的三条线段能首尾相接构成三角形的是( ).

A.1 cm,2 cm,3 cm
B.3 cm,4 cm,5 cm
C.4 cm,5 cm,10 cm
D.6 cm,9 cm,2 cm
名师启发 利用三角形的三边关系来进行判断.

答案： B　[解析]根据三角形的三边关系，得
A.1+2=3，不能构成三角形；B.3+4＞5，能构成三角形；C.4+5＜10，不能构成三角形；
D.2+6＜9，不能构成三角形.故选B.

例2 (2025·山东泰安泰山区期中)若三角形两边长分别为2,6,则该三角形第三边长$a$的取值范围是____.
名师启发 利用三角形三边关系列出不等式来解决问题.

答案： 4＜a＜8　[解析]
∵三角形两边长分别为2,6，该三角形第三边长为a，
∴6−2＜a＜6+2，解得4＜a＜8.

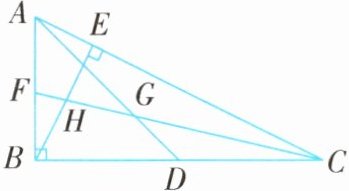
例3 (2025·安徽黄山期中)如图,$AD$,$BE$,$CF分别是\triangle ABC$的中线、高和角平分线,$\angle ABC = 90^{\circ}$,$CF交AD于点G$,交$BE于点H$,$AB = BD$. 下列结论：①$AB = CD$；②$FG = GC$；③$\angle ABE = 2\angle FCB$；④$\angle BFH = \angle BHF$. 其中一定正确的是( ).


A.①③④
B.②③④
C.①②③
D.①②④
名师启发 根据中线的定义判断①；根据角平分线的定义以及同角的余角相等判断③；根据等角的余角相等以及对顶角相等判断④,即可得出结论.
方法技巧
本题主要考查了三角形中线、角平分线及高的定义,结合相关知识灵活运用定义进行角度和线段长度的推算是解答此题的关键.

答案： A　[解析]
∵AD是△ABC的中线，
∴BD=CD.
∵AB=BD，
∴AB=CD，故①正确；
∵BE,CF分别是△ABC的高和角平分线，
∴∠AEB=∠BEC=90°，∠ACB=2∠ACF=2∠FCB，
∴∠ABE+∠BAC=90°，
∵∠ABC=90°，
∴∠ACB+∠BAC=90°，
∴∠ABE=∠ACB=2∠FCB，故③正确；
∵∠ABC=90°，∠BEC=90°，
∴∠BFC+∠FCB=90°，∠ECF+∠EHC=90°.
∵∠BCF=∠ECF，
∴∠BFH=∠CHE，
∵∠CHE=∠BHF，
∴∠BFH=∠BHF，故④正确；
条件不足，无法得到FG=GC，故②错误.
故选A