《2025年实验班提优训练八年级数学上册人教版》

8. (2025·福建福州十九中期末)如图,已知点$M是等边三角形ABC的边AB$上的一点,若$\angle AMC = 103^{\circ}$,则在以线段$AM$,$BM$,$CM$为边围成的三角形中,最小内角的度数为______$^{\circ}$.

答案：
17 [解析]如图所示，将△CBM 绕点 C 顺时针旋转 60°得到△CAQ，

∴CM=CQ，∠MCQ=60°，BM=AQ，∠AQC=∠BMC，
∴△CMQ 为等边三角形，
∴MQ=CM，∠CQM=60°，
∴以 AM，BM，CM 线段为边的三角形，即△AMQ，最小的锐角为∠AQM.
∵∠AMC=103°，
∴∠CMB=180° - 103°=77°，
∴∠CQA=∠CMB=77°，
∴∠AQM=∠CQA - ∠CQM=77° - 60°=17°.

9. (中考新考法 新定义问题)(2024·山东临沂经开区期末)定义：如果三角形有两个内角的差为$60^{\circ}$,那么这样的三角形叫作“准等边三角形”.已知$\triangle ABC$是“准等边三角形”,其中$\angle A = 50^{\circ}$,$\angle C＞90^{\circ}$,则$\angle B = $20°或 35°.

答案： 20°或 35° [解析]
∵△ABC 是“准等边三角形”，∠A=50°，∠C＞90°，
∴分两种情况：当∠C - ∠A=60°时，∠C=∠A+60°=110°，
∴∠B=180° - ∠C - ∠A=180° - 110° - 50°=20°；当∠C - ∠B=60°时，
∵∠A=50°，
∴∠C+∠B=180° - ∠A=130°，
∴2∠B=70°，
∴∠B=35°.综上所述，∠B 的度数为 20°或 35°.

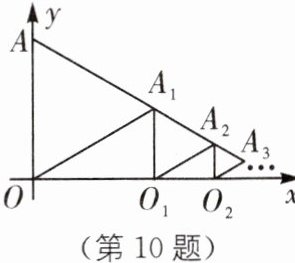
10. (2025·黑龙江绥化海伦期末)如图,在平面直角坐标系$xOy$中,已知点$A的坐标是(0,1)$,以$OA为边在右侧作等边三角形OAA_1$,过点$A_1作x$轴的垂线,垂足为点$O_1$,以$O_1A_1为边在右侧作等边三角形O_1A_1A_2$,再过点$A_2作x$轴的垂线,垂足为点$O_2$,以$O_2A_2为边在右侧作等边三角形O_2A_2A_3$,…$$,按此规律继续作下去,得到等边三角形$O_{2024}A_{2024}A_{2025}$,则点$A_{2025}$的纵坐标为______$(\frac{1}{2})^{2025}$.

答案： $(\frac{1}{2})^{2025}$ [解析]
∵三角形 OAA₁ 是等边三角形，
∴OA₁=OA=1，∠AOA₁=60°，
∴∠OO₁A₁=30°.在 Rt△O₁OA₁ 中，∠OO₁A₁=90°，∠O₁OA₁=30°，
∴O₁A₁=$\frac{1}{2}$OA₁=$\frac{1}{2}$，即点 A₁ 的纵坐标为 $\frac{1}{2}$；同理，O₂A₂=$\frac{1}{2}$O₁A₂=$(\frac{1}{2})^{2}$，O₃A₃=$\frac{1}{2}$O₂A₃=$(\frac{1}{2})^{3}$，即点 A₂ 的纵坐标为 $(\frac{1}{2})^{2}$，点 A₃ 的纵坐标为 $(\frac{1}{2})^{3}$，…，
∴点 A₂₀₂₅ 的纵坐标为 $(\frac{1}{2})^{2025}$.

11. (2025·福建南平期末)如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC = 100^{\circ}$,以$AC$为边,在$\triangle ABC的外部作等边三角形ACD$,$E是AC$的中点,连接$DE并延长交BC于F$.求$\angle DFC$的度数.

答案：
∵AB=AC，∠BAC=100°，
∴∠ABC=∠ACB=$\frac{180° - 100°}{2}$=40°.
∵△ACD 是等边三角形，E 是 AC 的中点，
∴DE⊥AC，
∴∠CEF=90°，
∴∠DFC+∠ACB=90°，
∴∠DFC=90° - ∠ACB=90° - 40°=50°.

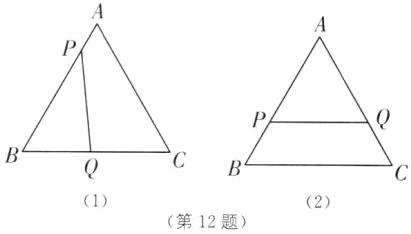
12. 在边长为$9的等边三角形ABC$中,点$Q是BC$上一点,点$P是AB$上一动点,以每秒$1个单位的速度从点A向点B$移动,设运动时间为$t$秒.
(1)如图(1),若$BQ = 6$,$PQ// AC$,求$t$的值.
(2)如图(2),若点$P从点A向点B$运动,同时点$Q以每秒2个单位的速度从点B经点C向点A$运动,当$t$为何值时,$\triangle APQ$为等边三角形?

答案：

(1)
∵△ABC 是等边三角形，
∴∠A=∠B=∠C=60°.
∵PQ//AC，
∴∠BQP=∠C=60°，∠BPQ=∠A=60°，
∴∠B=∠BQP=∠BPQ，
∴△BPQ 是等边三角形，
∴BP=BQ.由题意可知 AP=t，则 BP=9 - t，
∴9 - t=6，解得 t=3，
∴t 的值为 3.
(2)①如图
(1)，当点 Q 在边 BC 上时，此时△APQ 不可能为等边三角形；

②如图
(2)，当点 Q 在边 AC 上时，若△APQ 为等边三角形，则 AP=AQ，由题意可知 AP=t，BC+CQ=2t，
∴AQ=BC+AC - (BC+CQ)=9+9 - 2t=18 - 2t，即 18 - 2t=t，解得 t=6，
∴当 t=6 时，△APQ 为等边三角形.

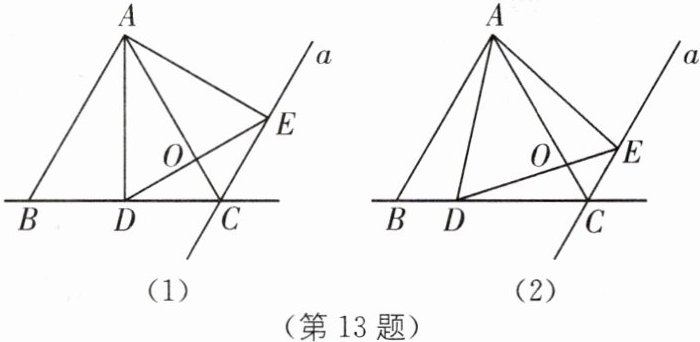
13. 如图,$\triangle ABC$为等边三角形,直线$a// AB$,$D为直线BC$上任一动点,将一$60^{\circ}角的顶点置于点D$处,它的一边始终经过点$A$,另一边与直线$a交于点E$.
(1)若$D恰好是BC$的中点(如图(1)),求证：$\triangle ADE$是等边三角形.
(2)若$D为直线BC$上任一点(如图(2)),其他条件不变,上述(1)的结论是否成立?若成立,请给予证明；若不成立,请说明理由.

答案：

(1)
∵a//AB，且△ABC 为等边三角形，
∴∠ACE=∠BAC=∠ABD=60°，AB=AC.
∵BD=CD，
∴AD⊥BC.
∵∠ADE=60°，
∴∠EDC=30°，
∴∠DOC=180° - ∠EDC - ∠ACB=90°，
∴∠DEC=∠DOC - ∠ACE=30°，
∴∠EDC=∠DEC，
∴EC=CD=DB，
∴△ABD≌△ACE(SAS)，
∴AD=AE，且∠ADE=60°，
∴△ADE 是等边三角形.
(2)成立.理由如下：如图，在 AC 上取点 F，使 CF=CD，连接 DF.

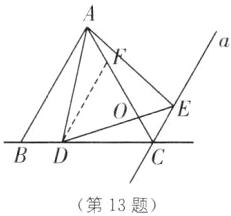
∵∠ACB=60°，
∴△DCF 是等边三角形.
∵∠ADF+∠FDE=∠EDC+∠FDE=60°，
∴∠ADF=∠EDC.
∵∠DAF+∠ADE=∠DEC+∠ACE，
∴∠DAF=∠DEC，
∴△ADF≌△EDC(AAS)，
∴AD=ED.又∠ADE=60°，
∴△ADE 是等边三角形.