第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
13. 在正方形ABCD中,$∠MAN= 45^{\circ },∠MAN$绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.如果$∠MAN$在如图(1)所示的位置时,有$BM+DN= MN$成立(不必证明).请问当$∠MAN$绕点A旋转到如图(2)所示的位置时,线段BM,DN和MN之间又有怎样的数量关系?请说明理由.
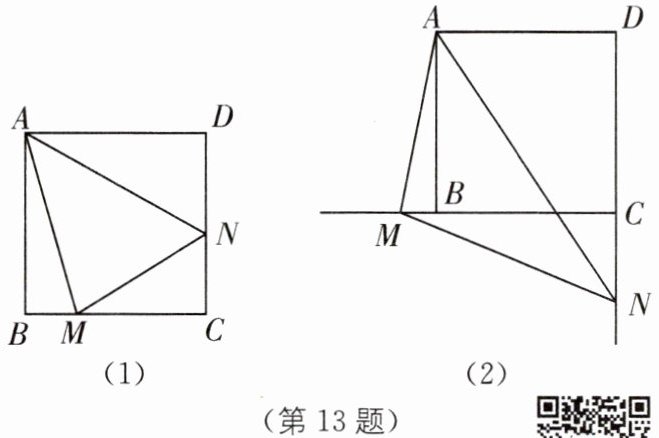

答案:
DN-BM=MN.理由如下:如图,在DC上截取DE=BM,连接AE. 在△ADE和△ABM中,$\left\{\begin{array}{l} AD=AB,\\ ∠ADE=∠ABM,\\ DE=BM,\end{array}\right. $
在△ADE和△ABM中,$\left\{\begin{array}{l} AD=AB,\\ ∠ADE=∠ABM,\\ DE=BM,\end{array}\right. $
∴△ADE≌△ABM(SAS),
∴AE=AM,∠1=∠4.
∵∠1+∠2=45°,
∴∠2+∠4=45°,
∴∠3=45°,
∴∠MAN=∠EAN.在△AEN和△AMN中,$\left\{\begin{array}{l} AE=AM,\\ ∠EAN=∠MAN,\\ AN=AN,\end{array}\right. $
∴△AEN≌△AMN(SAS),
∴MN=EN,
∴MN=EN=DN-DE=DN-BM.
DN-BM=MN.理由如下:如图,在DC上截取DE=BM,连接AE.
 在△ADE和△ABM中,$\left\{\begin{array}{l} AD=AB,\\ ∠ADE=∠ABM,\\ DE=BM,\end{array}\right. $
在△ADE和△ABM中,$\left\{\begin{array}{l} AD=AB,\\ ∠ADE=∠ABM,\\ DE=BM,\end{array}\right. $∴△ADE≌△ABM(SAS),
∴AE=AM,∠1=∠4.
∵∠1+∠2=45°,
∴∠2+∠4=45°,
∴∠3=45°,
∴∠MAN=∠EAN.在△AEN和△AMN中,$\left\{\begin{array}{l} AE=AM,\\ ∠EAN=∠MAN,\\ AN=AN,\end{array}\right. $
∴△AEN≌△AMN(SAS),
∴MN=EN,
∴MN=EN=DN-DE=DN-BM.
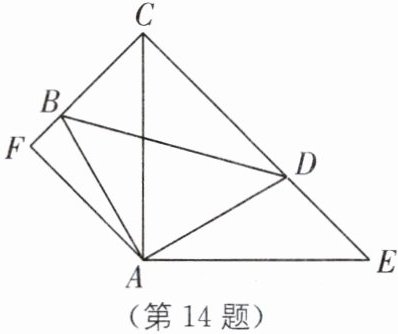
14. (2024·菏泽郓城一模)如图,$∠BAD= ∠CAE= 90^{\circ },AB= AD,AE= AC,AF⊥CB$,垂足为F.
(1)求证:$△ABC\cong △ADE;$
(2)求$∠FAE$的度数;
(3)求证:$CD= 2BF+DE.$
(1)求证:$△ABC\cong △ADE;$
(2)求$∠FAE$的度数;
(3)求证:$CD= 2BF+DE.$

答案:
(1)
∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,在△ABC和△ADE中,$\left\{\begin{array}{l} AB=AD,\\ ∠BAC=∠DAE,\\ AC=AE,\end{array}\right. $
∴△ABC≌△ADE(SAS).
(2)
∵∠CAE=90°,AC=AE,
∴∠E=45°.由
(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°.
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°.
(3)如图,延长BF到点G,使得FG=FB,连接GA.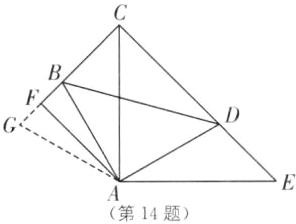
∵AF⊥BG,
∴∠AFG=∠AFB=90°,在△AFB和△AFG中,$\left\{\begin{array}{l} BF=GF,\\ ∠AFB=∠AFG,\\ AF=AF,\end{array}\right. $
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G.
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA.在△CGA和△CDA中,$\left\{\begin{array}{l} ∠GCA=∠DCA,\\ ∠CGA=∠CDA,\\ AG=AD,\end{array}\right. $
∴△CGA≌△CDA(AAS).
∴CG=CD.
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
(1)
∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,在△ABC和△ADE中,$\left\{\begin{array}{l} AB=AD,\\ ∠BAC=∠DAE,\\ AC=AE,\end{array}\right. $
∴△ABC≌△ADE(SAS).
(2)
∵∠CAE=90°,AC=AE,
∴∠E=45°.由
(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°.
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°.
(3)如图,延长BF到点G,使得FG=FB,连接GA.

∵AF⊥BG,
∴∠AFG=∠AFB=90°,在△AFB和△AFG中,$\left\{\begin{array}{l} BF=GF,\\ ∠AFB=∠AFG,\\ AF=AF,\end{array}\right. $
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G.
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA.在△CGA和△CDA中,$\left\{\begin{array}{l} ∠GCA=∠DCA,\\ ∠CGA=∠CDA,\\ AG=AD,\end{array}\right. $
∴△CGA≌△CDA(AAS).
∴CG=CD.
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
15. 一线三等角模型在$△ABC和△DCE$中,$CA= CB,CD= CE,∠CAB= ∠CED= α.$
(1)如图(1),将AD,EB延长,延长线相交于点O.
①求证:$BE= AD;$
②用含α的式子表示$∠BOA$的度数(直接写出结果);
(2)如图(2),当$α=45^{\circ }$时,连接BD,AE,作$CM⊥AE$于点M,延长MC与BD交于点N,求证:N是BD的中点.

(1)如图(1),将AD,EB延长,延长线相交于点O.
①求证:$BE= AD;$
②用含α的式子表示$∠BOA$的度数(直接写出结果);
(2)如图(2),当$α=45^{\circ }$时,连接BD,AE,作$CM⊥AE$于点M,延长MC与BD交于点N,求证:N是BD的中点.

答案:
(1)①
∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°-2α,∠DCE=180°-2α.
∴∠ACB=∠DCE.
∴∠ACB-∠DCB=∠DCE-∠DCB.
∴∠ACD=∠BCE.在△ACD和△BCE中,$\left\{\begin{array}{l} AC=BC,\\ ∠ACD=∠BCE,\\ DC=EC,\end{array}\right. $
∴△ACD≌△BCE(SAS).
∴BE=AD.②2α.
(2)如图,作BP⊥MN交MN的延长线于点P,作DQ⊥MN于点Q.构造两个一线三垂直模型
∵CA=CB,∠CAB=45°,
∴∠ACB=180°-2×45°=90°.
∵∠BCP+∠ACM=∠CAM+∠ACM=90°,
∴∠BCP=∠CAM. 在△CBP和△ACM中,$\left\{\begin{array}{l} ∠CPB=∠AMC,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right. $
在△CBP和△ACM中,$\left\{\begin{array}{l} ∠CPB=∠AMC,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right. $
∴△CBP≌△ACM(AAS),
∴MC=BP.同理可证CM=DQ,
∴DQ=BP.在△BPN和△DQN中,$\left\{\begin{array}{l} ∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right. $
∴△BPN≌△DQN(AAS).
∴BN=ND,
∴N是BD的中点.
(1)①
∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°-2α,∠DCE=180°-2α.
∴∠ACB=∠DCE.
∴∠ACB-∠DCB=∠DCE-∠DCB.
∴∠ACD=∠BCE.在△ACD和△BCE中,$\left\{\begin{array}{l} AC=BC,\\ ∠ACD=∠BCE,\\ DC=EC,\end{array}\right. $
∴△ACD≌△BCE(SAS).
∴BE=AD.②2α.
(2)如图,作BP⊥MN交MN的延长线于点P,作DQ⊥MN于点Q.构造两个一线三垂直模型
∵CA=CB,∠CAB=45°,
∴∠ACB=180°-2×45°=90°.
∵∠BCP+∠ACM=∠CAM+∠ACM=90°,
∴∠BCP=∠CAM.
 在△CBP和△ACM中,$\left\{\begin{array}{l} ∠CPB=∠AMC,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right. $
在△CBP和△ACM中,$\left\{\begin{array}{l} ∠CPB=∠AMC,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right. $∴△CBP≌△ACM(AAS),
∴MC=BP.同理可证CM=DQ,
∴DQ=BP.在△BPN和△DQN中,$\left\{\begin{array}{l} ∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right. $
∴△BPN≌△DQN(AAS).
∴BN=ND,
∴N是BD的中点.
查看更多完整答案,请扫码查看


