《2025年实验班提优训练八年级数学上册人教版》

3. (2025·广东广州番禺区期中)已知$a+b= 3,ab= -1$.求下列代数式的值:
(1)$a^{2}+b^{2};$
(2)$a-b.$

答案： 3.
(1)
∵(a + b)² = a² + b² + 2ab,
∴a² + b² = (a + b)² - 2ab = 3² - 2×(-1) = 11.
(2)
∵(a - b)² = a² + b² - 2ab = 11 - 2×(-1) = 13,
∴a - b = ±$\sqrt{13}$.

(1)若$(a+b)^{2}= 20,ab= 4$,则$a-b= $±2;
(2)若$x满足(65-x)^{2}+(x-50)^{2}= 325$,求$(65-x)(x-50)$的值;
-50
(3)如图,在长方形$ABCD$中,$AB= 12,BC= 8$,点$E,F分别是边AD,AB$上的点,且$DE= BF= a$,分别以$AE,AF为边在长方形ABCD外侧作正方形AEMN和正方形APQF$,若长方形$AFGE$的面积为56,求图中两个正方形的面积之和.
128

答案： 变式3.1
(1)±2 [解析]
∵(a + b)² = 20,ab = 4,
∴a² + 2ab + b² = 20,即a² + b² = 20 - 8 = 12,
∴(a - b)² = a² - 2ab + b² = 12 - 2×4 = 4,
∴a - b = ±2.
(2)
∵(65 - x)² + (x - 50)² = 325,
∴(65 - x)(x - 50)=$\frac{(65 - x + x - 50)² - [(65 - x)² + (x - 50)²]}{2}$=$\frac{15² - 325}{2}$ = -50.
(3)
∵AB = 12,BC = 8,且DE = BF = a,
∴AE = 8 - a,AF = 12 - a.
∵长方形AFGE的面积为56,
∴AE·AF = (8 - a)(12 - a) = 56.图中两个正方形的面积之和为(8 - a)² + (12 - a)² = [(8 - a) - (12 - a)]² + 2(8 - a)(12 - a)=(-4)² + 2×56 = 128.

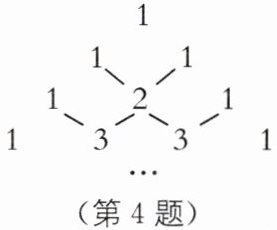
4. 我国宋朝数学家杨辉在其著作《详解九章算法》中提出“杨辉三角”(如图),揭示了$(a+b)^{n}$($n$为非负整数)展开式项数及各项系数的有关规律:杨辉三角两腰上的数都是1,其余每个数为它的上方(左右)两数之和,例如:
$(a+b)^{0}= 1$,它只有一项,系数为1;
$(a+b)^{1}= a+b$,它有两项,系数分别为1,1,系数和为2;
$(a+b)^{2}= a^{2}+2ab+b^{2}$,它有三项,中间项系数2等于上方数字1加1,系数分别为1,2,1,系数和为4;
$(a+b)^{3}= a^{3}+3a^{2}b+3ab^{2}+b^{3}$,它有四项,中间项系数3等于上方数字1加2,系数分别为1,3,3,1,系数和为8;…

(1)$(a+b)^{5}$的展开式的系数分别为1,5,10,10,5,1,系数和为2⁵;
(2)$(a+b)^{n}$展开式共有n + 1项,系数和为2ⁿ.

答案： 4.
(1)1,5,10,10,5,1 2⁵ [解析]根据杨辉三角可知,(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵,
∴(a + b)⁵的展开式的系数分别为1,5,10,10,5,1,
∴系数和为1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁵.
(2)n + 1 2ⁿ [解析](a + b)¹ = a + b,共有2项,系数分别为1,1;(a + b)² = a² + 2ab + b²,共有3项,系数分别为1,2,1;(a + b)³ = a³ + 3a²b + 3ab² + b³,共有4项,系数分别为1,3,3,1;(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴,共有5项,系数分别为1,4,6,4,1;…,
∴(a + b)ⁿ展开式中共有n + 1项.令(a + b)ⁿ中a = 1,b = 1,则(a + b)ⁿ的展开式中的每一项正好是每一项的系数,
∴(a + b)ⁿ的展开式中各项的系数和为(1 + 1)ⁿ = 2ⁿ.