《2025年实验班提优训练八年级数学上册人教版》

1. (2025·山东青岛莱西期中)计算$\frac {y}{x}÷\frac {y}{2}\cdot \frac {2}{y}$的结果是(A).
A.$\frac {4}{xy}$
B.$\frac {1}{2}x$
C.$\frac {y}{x}$
D.$2y$

答案： 1. A 解析 原式=$\frac{y}{x} \cdot \frac{2}{y} \cdot \frac{2}{y}=\frac{4}{xy}$. 故选 A.
易错警示 同级运算,按照从左到右的顺序进行,本题不能先做后面两式的乘法,否则就错了.

2. (2025·山东烟台栖霞期中)在下列四个算式中:
①$\frac {a}{y}\cdot \frac {x}{b}$;②$\frac {n}{m}\cdot \frac {2m}{n}$;③$\frac {4}{x}÷\frac {2}{x}$;④$\frac {a}{b^{2}}÷\frac {2a^{2}}{b^{2}}$,结果是分式的是(A).
A.①④
B.①③
C.②④
D.③④

答案： 2. A 解析 ①原式=$\frac{ax}{by}$,结果是分式;
②原式=2,结果不是分式;
③原式=$\frac{4}{x} \cdot \frac{x}{2}=2$,结果不是分式;
④原式=$\frac{a}{b^{2}} \cdot \frac{b^{2}}{2a^{2}}=\frac{1}{2a}$,结果是分式,
则其结果是分式的是①④. 故选 A.

3. 教材P146例1·变式 计算:$\frac {5x}{y}\cdot \frac {y}{15x^{2}}=$$\frac{1}{3x}$.

答案： 3. $\frac{1}{3x}$

4. (2024·大庆中考)若$a+\frac {1}{a}= \sqrt {5}$,则$a^{2}+\frac {1}{a^{2}}= $3.

答案： 4. 3 解析 $\because a+\frac{1}{a}=\sqrt{5}$,
$\therefore a^{2}+\frac{1}{a^{2}}=(a+\frac{1}{a})^{2}-2=(\sqrt{5})^{2}-2=3$.

5. (广东深圳实验中学自主招生)化简$\frac {x}{x-1}÷\frac {1}{1-x}$的结果为$-x$.

答案： 5. $-x$ 解析 原式=$\frac{x}{x-1} \cdot (1-x)=-x$.

6. (2025·山东济南钢城区期中)计算:
(1)$\frac {x+3}{x^{2}-2x+1}÷\frac {x^{2}+3x}{(x-1)^{2}}$;
(2)$\frac {x^{2}-4}{x+2}÷(x-2)\cdot \frac {1}{x-2}$.

答案： 6.
(1)$\frac{x+3}{x^{2}-2x+1} ÷ \frac{x^{2}+3x}{(x-1)^{2}}=\frac{x+3}{(x-1)^{2}} ÷ \frac{x(x+3)}{(x-1)^{2}}$
=$\frac{x+3}{(x-1)^{2}} \cdot \frac{(x-1)^{2}}{x(x+3)}=\frac{1}{x}$.
(2)$\frac{x^{2}-4}{x+2} ÷ (x-2) \cdot \frac{1}{x-2}$
=$\frac{(x+2)(x-2)}{x+2} \cdot \frac{1}{x-2} \cdot \frac{1}{x-2}=\frac{1}{x-2}$.

7. (2025·山东威海环翠区期中)下列各式中,计算结果正确的有(C).
①$\frac {3x}{x^{2}}\cdot \frac {x}{3x}= \frac {1}{x}$;②$a÷b×\frac {1}{b}= a$;③$\frac {a}{a^{2}-1}÷\frac {a^{2}}{a^{2}+a}= \frac {1}{a-1}$;④$8a^{2}b^{2}÷(-\frac {3a}{4b^{2}})= -6a^{3}b$;⑤$(-\frac {a^{2}}{b})\cdot (-\frac {b^{2}}{a})÷(ab)^{2}= \frac {1}{ab}$.
A.1个
B.2个
C.3个
D.4个

答案： 7. C 解析 ①$\frac{3x}{x^{2}} \cdot \frac{x}{3x}=\frac{1}{x}$,该选项计算正确,符合题意;
②$a ÷ b × \frac{1}{b}=\frac{a}{b^{2}}$,该选项计算错误,不符合题意;
③$\frac{a}{a^{2}-1} ÷ \frac{a^{2}}{a^{2}+a}=\frac{a}{(a+1)(a-1)} \cdot \frac{a(a+1)}{a^{2}}=\frac{1}{a-1}$,该选项计算正确,符合题意;
④$8a^{2}b^{2} ÷ (-\frac{3a}{4b^{2}})=8a^{2}b^{2} \cdot (-\frac{4b^{2}}{3a})=-\frac{32ab^{4}}{3}$,该选项计算错误,不符合题意;
⑤$(-\frac{a^{2}}{b}) \cdot (-\frac{b^{2}}{a}) ÷ (ab)^{2}=\frac{1}{ab}$,该选项计算正确,符合题意.综上,正确的有 3 个.故选 C.

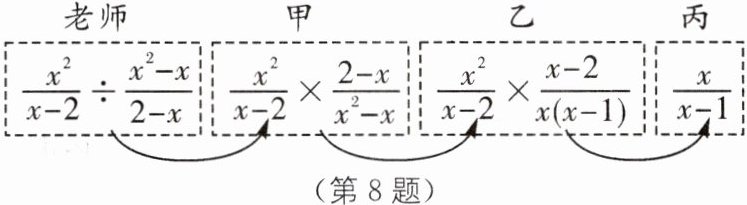
8. (2025·广东肇庆封开期末)某数学老师在课堂上设计了一个接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将计算结果传递给下一人,最后完成化简,过程如图所示.对于三个人的接力过程判断正确的是(C).

A.三个人都正确
B.甲有错误
C.乙有错误
D.丙有错误

答案： 8. C 解析 乙的分子由$2-x$变成了$x-2$,也就是分子乘了-1,而分母和分式本身的符号并没有发生变化,所以乙有错误.故选 C.
方法技巧 分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.

9. (2025·河北沧州南皮桂和中学期中)若$\frac {□}{a-b}÷\frac {3a}{a^{2}-b^{2}}$运算的结果是整式,则“□”内的式子可能是(A).
A.$ab$
B.$a+b$
C.$a-b$
D.$\frac {1}{a}$

答案： 9. A 解析 A.$\frac{ab}{a-b} ÷ \frac{3a}{a^{2}-b^{2}}=\frac{ab}{a-b} \cdot \frac{(a+b)(a-b)}{3a}=\frac{ab+b^{2}}{3}$,结果是整式,故此选项符合题意;
B.$\frac{a+b}{a-b} ÷ \frac{3a}{a^{2}-b^{2}}=\frac{a+b}{a-b} \cdot \frac{(a+b)(a-b)}{3a}=\frac{a^{2}+2ab+b^{2}}{3a}$,结果不是整式,故此选项不符合题意;
C.$\frac{a-b}{a-b} ÷ \frac{3a}{a^{2}-b^{2}}=1 × \frac{a^{2}-b^{2}}{3a}=\frac{a^{2}-b^{2}}{3a}$,结果不是整式,故此选项不符合题意;
D.$\frac{1}{a-b} ÷ \frac{3a}{a^{2}-b^{2}}=\frac{1}{a(a-b)} \cdot \frac{(a+b)(a-b)}{3a}=\frac{a+b}{3a^{2}}$,结果不是整式,故此选项不符合题意.故选 A.

10. (2025·吉林大学附中慧谷学校期末)如图,小谷的作业本上有一道填空题,其中有一部分被墨水污染了:
化简:$\frac {x-4}{x^{2}-9}÷\frac {□}{x-3}$的结果为____.
若被污染的部分是一个关于$x$的一次二项式,将其记为$A$,且该题化简的结果为$\frac {1}{x+3}$,求整式$A$.
$\frac{1}{x+3}$
$A=x-4$

答案： 10.$\frac{x-4}{x^{2}-9} ÷ \frac{□}{x-3}=\frac{x-4}{(x+3)(x-3)} × \frac{(x-3)}{□}$
=$\frac{x-4}{□(x+3)}$.
∵化简的结果为$\frac{1}{x+3}$,
∴$\frac{x-4}{□(x+3)}=\frac{1}{x+3}$,
∴$□=\frac{x-4}{x+3} ÷ \frac{1}{x+3}$,
∴$□=x-4$,即$A=x-4$.