《2025年实验班提优训练八年级数学上册人教版》

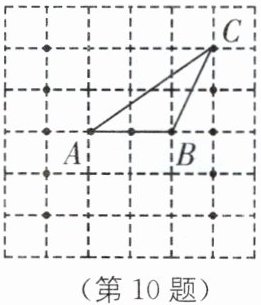
10. (2025·吉林第二实验学校期末)如图,在$6×6$的正方形网格中,选取13个格点,以其中的三个格点A,B,C为顶点画$△ABC$,请你在图中以选取的格点为顶点再画出一个$△ABP$,使$△ABP与△ABC$成轴对称,这样的点P有____个.(填点P的个数)

答案：
2 [解析]如图，满足条件的△ABP有2个.

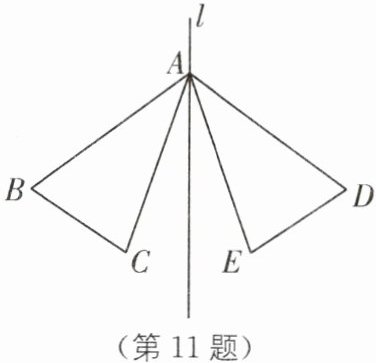
11. 如图,$△ABC和△ADE$关于直线l对称,已知$AB= 15,DE= 10,∠D= 70^{\circ }$.求$∠B$的度数及BC,AD的长度.

答案：
∵△ABC和△ADE关于直线l对称，
∴△ABC≌△ADE，
∴AB=AD，BC=DE，∠B=∠D.又AB=15，DE=10，∠D=70°，
∴∠B=70°，BC=10，AD=15.

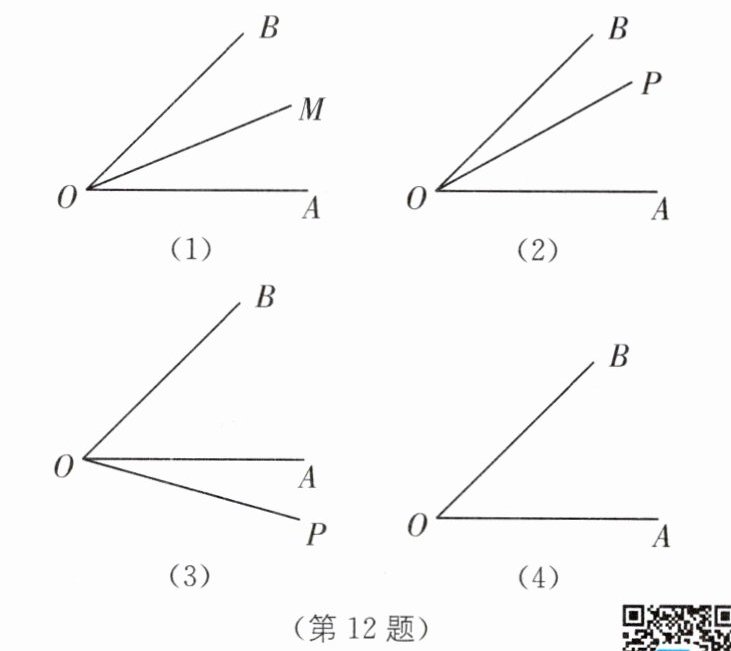
12. 分类讨论思想 [定义]如图(1),OM平分$∠AOB$,则称射线OB,OA关于OM对称.
[理解题意]
(1)如图(1),射线OB,OA关于OM对称且$∠AOB= 45^{\circ }$,则$∠AOM= $____度;
[应用实际]
(2)如图(2),若$∠AOB= 45^{\circ }$,OP在$∠AOB$内部,OP,$OP_{1}$关于OB对称,OP,$OP_{2}$关于OA对称,求$∠P_{1}OP_{2}$的度数;
(3)如图(3),若$∠AOB= 45^{\circ }$,OP在$∠AOB$外部,且$0^{\circ }＜∠AOP＜45^{\circ }$,OP,$OP_{1}$关于OB对称,OP,$OP_{2}$关于OA对称,求$∠P_{1}OP_{2}$的度数;
[拓展提升]
(4)如图(4),若$∠AOB= 45^{\circ }$,OP,$OP_{1}关于∠AOB$的OB边对称,$∠AOP_{1}= 4∠BOP_{1}$,求$∠AOP$的度数(直接写出答案).

答案：
（1）22.5 [解析]
∵射线OB，OA关于OM对称且∠AOB=45°，
∴∠AOM=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×45°=22.5°；（2）
∵OP和OP₁关于OB对称，
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称，
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁+∠POP₂，
∴∠P₁OP₂=2∠BOP+2∠AOP=2∠AOB=90°；（3）
∵OP和OP₁关于OB对称，
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称，
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁-∠POP₂，
∴∠P₁OP₂=2∠BOP-2∠AOP=2∠AOB=90°；（4）①若OP在∠AOB内部，如图（1）.
∵OP，OP₁关于OB对称，
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁，
∴∠AOB=3∠BOP₁=45°.
∴∠BOP₁=15°.
∴∠BOP=∠BOP₁=15°.
∴∠AOP=30°；②若OP在∠AOB外部，
∵∠AOP₁=4∠BOP₁，
∴射线OP在射线OB的上面，如图（2）.
∵OP，OP₁关于∠AOB的边OB对称，
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁，
∴∠AOB=∠BOP₁+∠AOP₁=5∠BOP₁=45°.
∴∠BOP₁=9°.
∴∠BOP=∠BOP₁=9°.
∴∠AOP=45°+9°=54°.综上所述，∠AOP的度数为30°或54°.

13. 传统文化 围棋 (2024·甘肃中考)围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点A或C的位置,则所得的对弈图是轴对称图形.(填写A,B,C,D中的一处即可,A,B,C,D位于棋盘的格点上)

答案： A或C [解析]白方如果落子于点A或C的位置，则所得的对弈图是轴对称图形.