第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 计算:
(1)$(3x-2y-1)^{2};$
(2)$(m+n)(m-n)-(m-2n)^{2}.$
(1)$(3x-2y-1)^{2};$
(2)$(m+n)(m-n)-(m-2n)^{2}.$
答案:
1.
(1)原式=[(3x - 2y) - 1]²=(3x - 2y)² - 2(3x - 2y) + 1=9x² - 12xy + 4y² - 6x + 4y + 1.
(2)原式=m² - n² - (m² - 4mn + 4n²)=m² - n² - m² + 4mn - 4n²=4mn - 5n².
(1)原式=[(3x - 2y) - 1]²=(3x - 2y)² - 2(3x - 2y) + 1=9x² - 12xy + 4y² - 6x + 4y + 1.
(2)原式=m² - n² - (m² - 4mn + 4n²)=m² - n² - m² + 4mn - 4n²=4mn - 5n².
变式1.1 运用平方差公式计算:
(1)$9.9×10.1;$ (2)$1003×997;$
(3)$(3+1)(3^{2}+1)(3^{4}+1)(3^{8}+1)(3^{16}+1).$
(1)$9.9×10.1;$ (2)$1003×997;$
(3)$(3+1)(3^{2}+1)(3^{4}+1)(3^{8}+1)(3^{16}+1).$
答案:
变式1.1
(1)原式=(10 - 0.1)×(10 + 0.1)=100 - 0.01=99.99.
(2)原式=(1000 + 3)×(1000 - 3)=1000000 - 9=999991.
(3)原式=$\frac{1}{2}$×(3 - 1)(3 + 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3² - 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3⁴ - 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3⁸ - 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3¹⁶ - 1)(3¹⁶ + 1)=$\frac{1}{2}$(3³² - 1).
(1)原式=(10 - 0.1)×(10 + 0.1)=100 - 0.01=99.99.
(2)原式=(1000 + 3)×(1000 - 3)=1000000 - 9=999991.
(3)原式=$\frac{1}{2}$×(3 - 1)(3 + 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3² - 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3⁴ - 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3⁸ - 1)(3⁸ + 1)(3¹⁶ + 1)=$\frac{1}{2}$(3¹⁶ - 1)(3¹⁶ + 1)=$\frac{1}{2}$(3³² - 1).
2. 比较$a^{2}+b^{2}与2ab$的大小.
尝试:(用“<”“=”或“>”填空)
①当$a= -1,b= -2$时,$a^{2}+b^{2}$
②当$a= 2,b= 5$时,$a^{2}+b^{2}$
③当$a= b= 3$时,$a^{2}+b^{2}$
验证:若$a,b$取任意实数,$a^{2}+b^{2}与2ab$有怎样的大小关系?试说明理由.
应用:当$a+b= 6,a^{2}+b^{2}= 30$时,请直接写出$a^{2}+9b^{2}-1$的最小值.
尝试:(用“<”“=”或“>”填空)
①当$a= -1,b= -2$时,$a^{2}+b^{2}$
>
$2ab;$②当$a= 2,b= 5$时,$a^{2}+b^{2}$
>
$2ab;$③当$a= b= 3$时,$a^{2}+b^{2}$
=
$2ab.$验证:若$a,b$取任意实数,$a^{2}+b^{2}与2ab$有怎样的大小关系?试说明理由.
应用:当$a+b= 6,a^{2}+b^{2}= 30$时,请直接写出$a^{2}+9b^{2}-1$的最小值.
17
答案:
2.尝试:①> [解析]
∵a = -1,b = -2,
∴a² + b² = 5,2ab = 4,
∴a² + b²>2ab.
②> [解析]
∵a = 2,b = 5,
∴a² + b² = 29,2ab = 20,
∴a² + b²>2ab.
③= [解析]
∵a = b = 3,
∴a² + b² = 18,2ab = 18,
∴a² + b² = 2ab.
验证:a² + b²≥2ab.理由如下:
∵(a - b)²≥0,即a² - 2ab + b²≥0,
∴a² + b²≥2ab.
应用:
∵a + b = 6,a² + b² = 30,
∴(a + b)²=a² + 2ab + b² = 36,
∴ab = 3.根据验证的结论,得a² + 9b²≥6ab,即a² + 9b²≥18,
∴a² + 9b² - 1≥18 - 1,
∴a² + 9b² - 1的最小值为18 - 1 = 17.
∵a = -1,b = -2,
∴a² + b² = 5,2ab = 4,
∴a² + b²>2ab.
②> [解析]
∵a = 2,b = 5,
∴a² + b² = 29,2ab = 20,
∴a² + b²>2ab.
③= [解析]
∵a = b = 3,
∴a² + b² = 18,2ab = 18,
∴a² + b² = 2ab.
验证:a² + b²≥2ab.理由如下:
∵(a - b)²≥0,即a² - 2ab + b²≥0,
∴a² + b²≥2ab.
应用:
∵a + b = 6,a² + b² = 30,
∴(a + b)²=a² + 2ab + b² = 36,
∴ab = 3.根据验证的结论,得a² + 9b²≥6ab,即a² + 9b²≥18,
∴a² + 9b² - 1≥18 - 1,
∴a² + 9b² - 1的最小值为18 - 1 = 17.
变式2.1 [提出问题]利用“图形”能够证明“等式”,如“完全平方公式”“平方差公式”都可以用图形进行证明,那么“图形”能否证明“不等式”呢?请完成以下探究性学习内容.
[自主探究]
用直角边分别为$a和b$的两个等腰直角三角形进行拼图,由图(1)得到图(2).
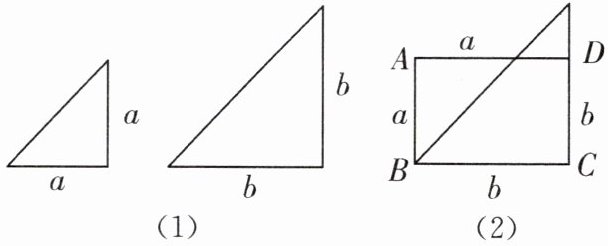
(1)请你仔细观察图形变化,解决下列问题.
①图(1)中两个三角形的面积分别为____和____,图(2)中长方形$ABCD$的面积为____.(用含$a,b$的字母表示)
②当$a≠b$时,比较大小:$\frac {a^{2}+b^{2}}{2}$____$ab$.(填“>”或“<”)
③当$a和b$满足什么条件时,$\frac {a^{2}+b^{2}}{2}与ab$相等?
甲同学说:我可以通过计算进行说明.乙同学说:我可以通过画图进行说明.请你选择其中一人的方法,进行说明.
[知识应用]
(2)已知$m>0,n>1$,且$m(n-1)= 9$,利用(1)发现的结论求$m^{2}+(n-1)^{2}$的最小值.
[自主探究]
用直角边分别为$a和b$的两个等腰直角三角形进行拼图,由图(1)得到图(2).
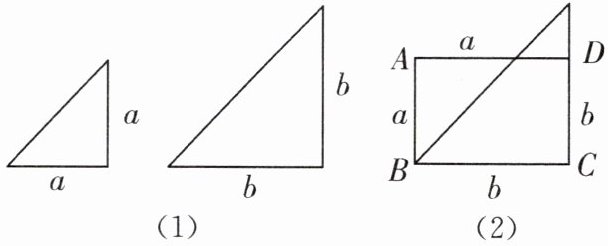
(1)请你仔细观察图形变化,解决下列问题.
①图(1)中两个三角形的面积分别为____和____,图(2)中长方形$ABCD$的面积为____.(用含$a,b$的字母表示)
②当$a≠b$时,比较大小:$\frac {a^{2}+b^{2}}{2}$____$ab$.(填“>”或“<”)
③当$a和b$满足什么条件时,$\frac {a^{2}+b^{2}}{2}与ab$相等?
甲同学说:我可以通过计算进行说明.乙同学说:我可以通过画图进行说明.请你选择其中一人的方法,进行说明.
[知识应用]
(2)已知$m>0,n>1$,且$m(n-1)= 9$,利用(1)发现的结论求$m^{2}+(n-1)^{2}$的最小值.
答案:
变式2.1
(1)①$\frac{1}{2}$a² $\frac{1}{2}$b² ab ②>
③当a = b时,$\frac{a² + b²}{2}$ = ab,
甲同学:当a = b时,$\frac{a² + b²}{2}$ = $\frac{a² + a²}{2}$ = a²,ab = a·a = a²,
∴当a = b时,$\frac{a² + b²}{2}$ = ab;
乙同学:

如图,当a = b时,$\frac{a² + b²}{2}$ = ab.
(2)由
(1)得$\frac{m² + (n - 1)²}{2}$≥m(n - 1),
∴$\frac{m² + (n - 1)²}{2}$≥9,
∴m² + (n - 1)²≥18,
∴m² + (n - 1)²的最小值为18.
变式2.1
(1)①$\frac{1}{2}$a² $\frac{1}{2}$b² ab ②>
③当a = b时,$\frac{a² + b²}{2}$ = ab,
甲同学:当a = b时,$\frac{a² + b²}{2}$ = $\frac{a² + a²}{2}$ = a²,ab = a·a = a²,
∴当a = b时,$\frac{a² + b²}{2}$ = ab;
乙同学:

如图,当a = b时,$\frac{a² + b²}{2}$ = ab.
(2)由
(1)得$\frac{m² + (n - 1)²}{2}$≥m(n - 1),
∴$\frac{m² + (n - 1)²}{2}$≥9,
∴m² + (n - 1)²≥18,
∴m² + (n - 1)²的最小值为18.
查看更多完整答案,请扫码查看


