《2025年实验班提优训练八年级数学上册人教版》

2. (第二十二届“华杯赛”初赛)如图,$AB= AC$,$AP= BQ$,$AO= BO= CO$,$\angle AQO= 16^{\circ}$,则$\angle CPO$等于(A).

A.$16^{\circ}$
B.$32^{\circ}$
C.$45^{\circ}$
D.$46^{\circ}$

答案： A

3. (第十五届WMO选拔赛复赛)如图,正三角形$ABC$的三边表示三面镜子,$BP= \frac{1}{3}AB= 1$,一束光线从点$P发射至BC上R$点,且$\angle BPR= 60^{\circ}$.光线依次经$BC$反射,$AC$反射,$AB$反射,…,一直继续下去.当光线第一次回到点$P$时,这束光线所经过的路线的总长为(B).
A.$6$
B.$9$
C.$18$
D.$27$

答案： B　[解析]
∵BP = $\frac{1}{3}$AB = 1,∠BPR = 60°,
∴PR = 1.根据等边三角形的性质可知当光线第一次回到点P时,光线经过的大致路线如图所示,
∴当第一次回到点P时,这束光线所经过的路线的总长为1 + 2 + 1 + 2 + 1 + 2 = 9.

4. (上海浦东新区自主招生)如图所示,在$\triangle ABC$中,$AB= AC$,点$P$,$Q分别在AC$,$AB$上,且$AP= PQ= QB= BC$,则$\angle A= $20°.

答案： 20°

5. 正三角形$ABC所在的平面内有一点P$,使得$\triangle PAB$,$\triangle PBC$,$\triangle PCA$都是等腰三角形,则这样的点$P$有10个.

答案： 10

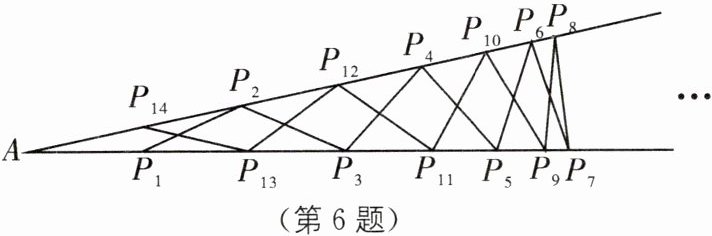
6. (全国初中数学竞赛初赛)在如图所示的钢架中,要焊上等长的$13$根钢条来加固钢架,若$AP_1= P_1P_2= P_2P_3=… =P_{13}P_{14}= P_{14}A$,则$\angle A$的度数是______12°.

答案： 12°

7. 如图,$\triangle ABC$是等边三角形,$\triangle BDC是顶角\angle BDC= 120^{\circ}$的等腰三角形,点$M是AB$延长线上的一点,点$N是CA$延长线上的一点,且$\angle MDN= 60^{\circ}$.试探究$BM$,$MN$,$CN$之间的数量关系,并给出证明.

答案： CN = MN + BM.证明如下:
如图,在CN上截取点E,使CE = BM,连接DE.
∵△ABC为等边三角形,
∴∠ACB = ∠ABC = 60°.
又△BDC为等腰三角形,且∠BDC = 120°,
∴BD = DC,∠DBC = ∠BCD = 30°.
∴∠ABD = ∠ABC + ∠DBC = ∠ACB + ∠BCD = ∠ECD = 90°,
∴∠MBD = 90°.
在△MBD与△ECD中,{BD = CD,∠MBD = ∠ECD,BM = CE}
∴△MBD≌△ECD(SAS).
∴MD = DE,∠MDB = ∠EDC.
又∠MDN = 60°,∠BDC = 120°,
∴∠EDN = ∠BDC - (∠BDN + ∠EDC) = ∠BDC - (∠BDN + ∠MDB) = ∠BDC - ∠MDN = 120° - 60° = 60°.
∴∠MDN = ∠EDN.
在△MND与△END中,{ND = ND,∠MDN = ∠EDN,MD = ED}
∴△MND≌△END(SAS).
∴NM = NE.
∴CN = NE + CE = MN + BM.

8. 如图,在等边三角形$ABC$中,$AE= CD$,$AD$,$BE交于点P$,$BQ\perp AD于点Q$.
(1)求证：$BP= 2PQ$；
(2)连接$PC$,若$BP\perp PC$,求$\frac{AP}{PQ}$的值.

答案：
(1)
∵△ABC是等边三角形,
∴AB = AC,∠BAE = ∠ACD = 60°.
在△BAE和△ACD中,{AB = CA,∠BAE = ∠ACD,AE = CD}
∴△BAE≌△ACD(SAS).
∴∠ABE = ∠CAD.
∴∠BPQ = ∠ABE + ∠BAP = ∠CAD + ∠BAP = ∠BAC = 60°.
∵BQ⊥AD,
∴∠PBQ = 30°.
∴BP = 2PQ.
(2)
∵∠ABE = ∠CAD,
∴∠ABC - ∠ABE = ∠BAC - ∠CAD,
即∠PBC = ∠BAQ.
∵BP⊥PC,
∴∠CPB = 90°.
在△BAQ和△CBP中,{∠BQA = ∠CPB,∠BAQ = ∠CBP,AB = BC}
∴△BAQ≌△CBP(AAS).
∴AQ = BP = 2PQ.
∴AP = PQ,即$\frac{AP}{PQ}$ = 1.

9. (浙江温州苍南提前招生)如图,三个等腰直角三角形$ADC$,$DPE$,$BEC的直角顶点分别为D$,$P$,$E$,且它们直角边长度均不相等,$CD不平行于PE$,求证：$P是AB$的中点.

答案： 如图,延长DC,EP交于点F,连接AF,AP,BP,
在等腰直角三角形ADC中,AD = CD,∠ADC = 90°,
∴∠ADF = ∠CDE = 90°.
在等腰直角三角形DPE中,∠DPE = 90°,DP = EP,
∴∠DEP = 45°,
∴∠EFD = 90° - ∠DEP = 45°,
∴△DEF为等腰直角三角形,
∴DE = DF,EP = FP.
易证得△ADF≌△CDE,{AD = CD,∠ADF = ∠CDE,DF = DE}
∴AF = CE,∠AFD = ∠CED,
∴∠FAD + ∠CED = ∠FAD + ∠AFD = 90°.
∵等腰直角三角形BEC中,CE = BE,∠BEC = 90°,
∴AF = BE,∠FAD + ∠CED + ∠BEC = 180°,
∴AF//BE.
∴∠AFP = ∠BEP,
∴△AFP≌△BEP,{AF = BE,∠AFP = ∠BEP,FP = EP}
∴AP = BP,∠APF = ∠BPE,
∴点P在AB上,
∴P是AB的中点.