第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. (2025·北京期末)在平面直角坐标系xOy中,点$(2,3)$关于y轴的对称点坐标是(
A.$(2,-3)$
B.$(-2,3)$
C.$(-2,-3)$
D.$(3,2)$
B
).A.$(2,-3)$
B.$(-2,3)$
C.$(-2,-3)$
D.$(3,2)$
答案:
1.B [解析]在平面直角坐标系xOy中,点(2,3)关于y轴的对称点坐标是(-2,3).故选B
2. (2025·江苏南京师大附中宿迁分校期末)已知点$A(a,2024)与点B(2025,b)$关于x轴对称,则$a+b$的值为(
A.1
B.-1
C.2
D.-2
A
).A.1
B.-1
C.2
D.-2
答案:
2.A [解析]由条件可知a=2025,b=-2024,
∴a+b=2025+(-2024)=1.故选A.
名师点评 对称点的坐标规律:①关于x轴对称的点,横坐标相同,纵坐标互为相反数;②关于y轴对称的点,纵坐标相同,横坐标互为相反数;③关于原点对称的点,横坐标与纵坐标都互为相反数.
∴a+b=2025+(-2024)=1.故选A.
名师点评 对称点的坐标规律:①关于x轴对称的点,横坐标相同,纵坐标互为相反数;②关于y轴对称的点,纵坐标相同,横坐标互为相反数;③关于原点对称的点,横坐标与纵坐标都互为相反数.
3. 教材P75练习T1·变式(2025·江苏南通如东期末)在平面直角坐标系xOy中,点$P(3,5)$关于y轴对称的点的坐标是
(-3,5)
.
答案:
3.(-3,5) [解析]在平面直角坐标系xOy中,点P(3,5)关于y轴的对称点的坐标是(-3,5).
4. 已知点$A(-3,2a-1)$,点$B(-a,a-3)$.
(1)若点A在第二、四象限的角平分线上,求点A关于y轴的对称点$A'$的坐标;
(2)若线段$AB// x$轴,求线段AB的长度;
(3)若点B到x轴的距离是到y轴距离的2倍,求点B的坐标.
(1)若点A在第二、四象限的角平分线上,求点A关于y轴的对称点$A'$的坐标;
(2)若线段$AB// x$轴,求线段AB的长度;
(3)若点B到x轴的距离是到y轴距离的2倍,求点B的坐标.
答案:
4.
(1)
∵点A在第二、四象限的角平分线上,
∴-3+2a-1=0,
∴a=2.
∴A(-3,3),
∴点A关于y轴的对称点A'的坐标为(3,3).
(2)
∵线段AB//x轴,
∴2a-1=a-3,
∴a=-2,
∴A(-3,-5),B(2,-5),
∴AB=2-(-3)=2+3=5.
(3)
∵点B到x轴的距离是到y轴距离的2倍,
∴2×|-a|=|a-3|,
∴a=1或a=-3,
∴B(-1,-2)或B(3,-6).
(1)
∵点A在第二、四象限的角平分线上,
∴-3+2a-1=0,
∴a=2.
∴A(-3,3),
∴点A关于y轴的对称点A'的坐标为(3,3).
(2)
∵线段AB//x轴,
∴2a-1=a-3,
∴a=-2,
∴A(-3,-5),B(2,-5),
∴AB=2-(-3)=2+3=5.
(3)
∵点B到x轴的距离是到y轴距离的2倍,
∴2×|-a|=|a-3|,
∴a=1或a=-3,
∴B(-1,-2)或B(3,-6).
5. 传统文化 剪纸(2025·河北邢台任泽区期中)剪纸艺术是最古老的中国民间艺术之一,很多剪纸
作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,若点E的坐标为$(2m,-n)$,其关于y轴对称的点F的坐标为$(3-n,-m+1)$,则$(m-n)^{2}$的值为(
A.9
B.-1
C.1
D.0

作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,若点E的坐标为$(2m,-n)$,其关于y轴对称的点F的坐标为$(3-n,-m+1)$,则$(m-n)^{2}$的值为(
C
).A.9
B.-1
C.1
D.0
答案:
5.C [解析]
∵E(2m,-n),F(3-n,-m+1)关于y轴对称,
∴{-n=-m+1,2m=n-3},解得{m=-4,n=-5},
∴(m-n)²=(-4+5)²=1.故选C.
∵E(2m,-n),F(3-n,-m+1)关于y轴对称,
∴{-n=-m+1,2m=n-3},解得{m=-4,n=-5},
∴(m-n)²=(-4+5)²=1.故选C.
6. 若点$P(a+1,2-2a)$关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为( ).


答案:
6.C [解析]
∵点P(a+1,2-2a)关于x轴的对称点在第四象限,
∴点P在第一象限.
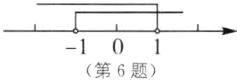
∴{a+1>0,2-2a>0},解得-1<a<1.
在数轴上表示如图
故选C;
6.C [解析]
∵点P(a+1,2-2a)关于x轴的对称点在第四象限,
∴点P在第一象限.

∴{a+1>0,2-2a>0},解得-1<a<1.
在数轴上表示如图
故选C;
7. 将点$A(2,1)变换到点B(2,-1)$,写出一种轴对称或平移方法:
向下平移2个单位长度或关于x轴对称
.
答案:
7.向下平移2个单位长度或关于x轴对称
8. (2025·重庆合川区期末)如图,$△ABC的三个顶点的坐标分别为A(-4,4),B(2,3),C(-1,1)$.
(1)作出$△ABC$关于x轴对称的$△A_{1}B_{1}C_{1}$并写出其顶点坐标;
(2)在(1)的条件下确定一点P,使得$PA= PA_{1}且PB= PB_{1}$,直接写出点P的坐标.
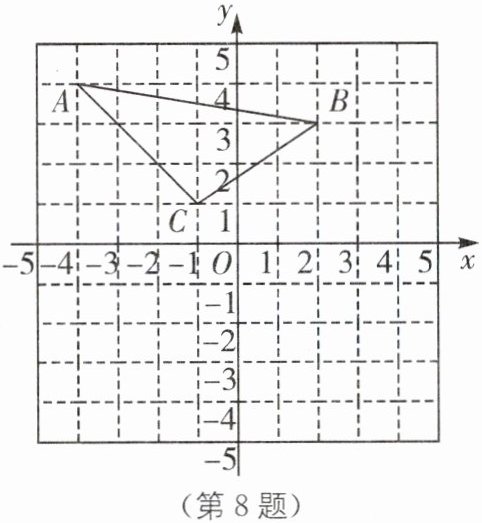
(1)作出$△ABC$关于x轴对称的$△A_{1}B_{1}C_{1}$并写出其顶点坐标;
(2)在(1)的条件下确定一点P,使得$PA= PA_{1}且PB= PB_{1}$,直接写出点P的坐标.

答案:
8.
(1)如图,△A₁B₁C₁即为所求;

A₁(-4,-4),B₁(2,-3),C₁(-1,-1).
(2)由对称性质可知,x轴上任意一点到A,A₁的距离相等,到B,B₁的距离相等,
∴P点坐标可以为(1,0)(答案不唯一).
8.
(1)如图,△A₁B₁C₁即为所求;

A₁(-4,-4),B₁(2,-3),C₁(-1,-1).
(2)由对称性质可知,x轴上任意一点到A,A₁的距离相等,到B,B₁的距离相等,
∴P点坐标可以为(1,0)(答案不唯一).
查看更多完整答案,请扫码查看


