第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. (2024·绵阳中考)如图,在$\triangle ABC$中,$AB= 5$,AD平分$∠BAC$交 BC 于点 D,$DE⊥AC$,垂足为 E,$\triangle ABD$的面积为 5,则 DE 的长为( ).

A.1
B.2
C.3
D.5

A.1
B.2
C.3
D.5
答案:
B [解析]过点D作DF⊥AB于F,如图
∵AD平分∠BAC,DE⊥AC,DF⊥AB,
∴DE=DF.
∵△ABD的面积为5,
∴$\frac{1}{2}$AB·DF=5.
∵AB=5,
∴DF=2,
∴DE=2.故选B.
方法技巧 解答本题需要过角平分线上的点作AB的垂线段,构造角平分线的基本图形,然后再用面积来进行计算.
B [解析]过点D作DF⊥AB于F,如图

∵AD平分∠BAC,DE⊥AC,DF⊥AB,
∴DE=DF.
∵△ABD的面积为5,
∴$\frac{1}{2}$AB·DF=5.
∵AB=5,
∴DF=2,
∴DE=2.故选B.
方法技巧 解答本题需要过角平分线上的点作AB的垂线段,构造角平分线的基本图形,然后再用面积来进行计算.
2. (2025·湖北武汉期末)如图,已知$\triangle ABC$的周长是18,$∠ABC和∠ACB$的平分线交于点 O,$OD⊥BC$于点 D,若$OD= 3$,则$\triangle ABC$的面积是____.


答案:
27 [解析]过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,如图所示.

∵点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC,
∴OE=OD=OF.
∵OD=3,△ABC的周长为18,
∴S△ABC=S△AOB+S△AOC+S△BOC
=$\frac{1}{2}$AB·OE+$\frac{1}{2}$AC·OF+$\frac{1}{2}$BC·OD
=$\frac{1}{2}$(AB+AC+BC)·OD=$\frac{1}{2}$×18×3=27.
名师点评 本题运用了“等积法”:对于一个几何图形,如果我们从不同的角度来分别计算图形的面积,这样就可以把几何图形的数量关系用等式表示出来,这样就能求出与垂线段有关的计算,或是能把一些重要的代数结论找出来.
27 [解析]过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,如图所示.

∵点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC,
∴OE=OD=OF.
∵OD=3,△ABC的周长为18,
∴S△ABC=S△AOB+S△AOC+S△BOC
=$\frac{1}{2}$AB·OE+$\frac{1}{2}$AC·OF+$\frac{1}{2}$BC·OD
=$\frac{1}{2}$(AB+AC+BC)·OD=$\frac{1}{2}$×18×3=27.
名师点评 本题运用了“等积法”:对于一个几何图形,如果我们从不同的角度来分别计算图形的面积,这样就可以把几何图形的数量关系用等式表示出来,这样就能求出与垂线段有关的计算,或是能把一些重要的代数结论找出来.
3. 如图所示,已知$\triangle ABC$,用直尺和圆规作$∠C$的平分线 CE.(保留作图痕迹,不要求写作法)
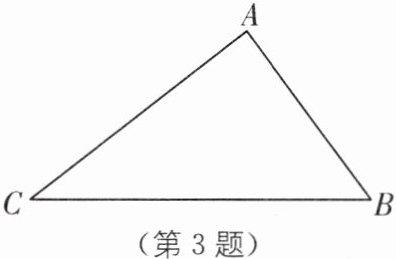

答案:
如图所示.

如图所示.

4. 教材 P50 练习 T2·变式 如图,在$\triangle ABC$中,$∠C= 90^{\circ }$,AD 平分$∠CAB,DE⊥AB$于点 E,点 F在边 AC 上,$BE= FC$.求证:$BD= DF$.
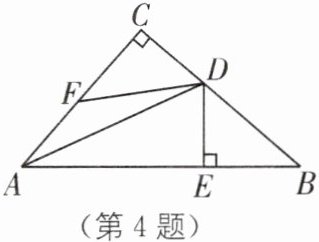

答案:
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DC=DE.
在△DCF和△DEB中,$\left\{\begin{array}{l} DC=DE,\\ ∠C=∠BED,\\ CF=EB,\end{array}\right. $
∴△DCF≌△DEB(SAS).
∴BD=DF.
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DC=DE.
在△DCF和△DEB中,$\left\{\begin{array}{l} DC=DE,\\ ∠C=∠BED,\\ CF=EB,\end{array}\right. $
∴△DCF≌△DEB(SAS).
∴BD=DF.
5. (2025·湖北孝感安陆期中)如图,点 I 是$\triangle ABC$三条角平分线的交点,$\triangle ABI的面积记为S_{1},\triangle ACI的面积记为S_{2},\triangle BCI的面积记为S_{3}$,且$S_{3}= 10$,关于$S_{1}+S_{2}$的值可能为(
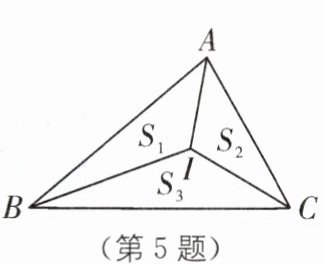
A.8
B.10
C.14
D.以上都有可能
C
).
A.8
B.10
C.14
D.以上都有可能
答案:
C [解析]
∵点I是△ABC三条角平分线的交点,
∴△ABI,△ACI和△BCI的边AB,AC和BC边上的高相等.
设△ABI,△ACI和△BCI的高为h,
∴S₁+S₂=$\frac{1}{2}$AB·h+$\frac{1}{2}$AC·h=$\frac{1}{2}$(AB+AC)h,S₃=$\frac{1}{2}$BC·h.
由三角形三边关系得AB+AC>BC,
∴S₁+S₂>S₃.
∵S₃=10,
∴S₁+S₂>10,故S₁+S₂的值可能为14,选项C符合题意,选项A,B,D不符合题意.故选C.
思路引导 解答本题的突破口是需要根据角平分线的性质得出△ABI,△ACI和△BCI的边AB,AC和BC边上的高相等,然后再利用面积法来解决问题.
∵点I是△ABC三条角平分线的交点,
∴△ABI,△ACI和△BCI的边AB,AC和BC边上的高相等.
设△ABI,△ACI和△BCI的高为h,
∴S₁+S₂=$\frac{1}{2}$AB·h+$\frac{1}{2}$AC·h=$\frac{1}{2}$(AB+AC)h,S₃=$\frac{1}{2}$BC·h.
由三角形三边关系得AB+AC>BC,
∴S₁+S₂>S₃.
∵S₃=10,
∴S₁+S₂>10,故S₁+S₂的值可能为14,选项C符合题意,选项A,B,D不符合题意.故选C.
思路引导 解答本题的突破口是需要根据角平分线的性质得出△ABI,△ACI和△BCI的边AB,AC和BC边上的高相等,然后再利用面积法来解决问题.
6. (2025·浙江湖州龙山中学月考)如图,$\triangle ABC$的角平分线 BD,CE 交于点 O,延长 BC 至 F,CG 与BD 的延长线相交于点 G,且$∠A= 2∠G,OD:DG= 3:4$,若$\triangle DOC$的面积为 6,$CG= 10$,则线段 CO 的长度为____.
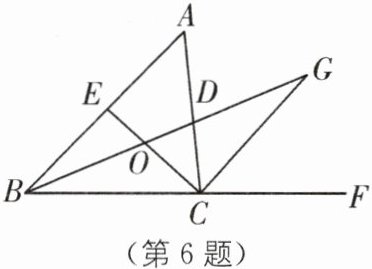

答案:
$\frac{14}{5}$ [解析]设∠G=α,∠ABD=β,过点C作CQ⊥BD于Q.

∵BD平分∠ABC,∠A=2∠G,
∴∠ABC=2β,∠DBC=∠ABD=β,∠A=2∠G=2α,
∴∠ACF=∠A+∠ABC=2α+2β,∠GCF=∠G+∠GBC=α+β,
∴∠ACG=∠GCF=$\frac{1}{2}$∠ACF.
∵CE平分∠ACB,
∴∠ACE=∠BCE=$\frac{1}{2}$∠ACB,
∴∠ECG=$\frac{1}{2}$(∠ACB+∠ACF)=90°.
∵S△ODC=$\frac{1}{2}$OD·CQ,S△CDG=$\frac{1}{2}$DG·CQ,OD:DG=3:4,
∴S△ODC:S△CDG=OD:DG=3:4.
∵△DOC的面积为6,
∴S△CDG=8,
∴S△OCG=S△ODC+S△CDG=14.
∵∠ECG=90°,
∴S△OCG=$\frac{1}{2}$OC·CG=$\frac{1}{2}$×10×OC=14,
∴OC=$\frac{14}{5}$.
$\frac{14}{5}$ [解析]设∠G=α,∠ABD=β,过点C作CQ⊥BD于Q.

∵BD平分∠ABC,∠A=2∠G,
∴∠ABC=2β,∠DBC=∠ABD=β,∠A=2∠G=2α,
∴∠ACF=∠A+∠ABC=2α+2β,∠GCF=∠G+∠GBC=α+β,
∴∠ACG=∠GCF=$\frac{1}{2}$∠ACF.
∵CE平分∠ACB,
∴∠ACE=∠BCE=$\frac{1}{2}$∠ACB,
∴∠ECG=$\frac{1}{2}$(∠ACB+∠ACF)=90°.
∵S△ODC=$\frac{1}{2}$OD·CQ,S△CDG=$\frac{1}{2}$DG·CQ,OD:DG=3:4,
∴S△ODC:S△CDG=OD:DG=3:4.
∵△DOC的面积为6,
∴S△CDG=8,
∴S△OCG=S△ODC+S△CDG=14.
∵∠ECG=90°,
∴S△OCG=$\frac{1}{2}$OC·CG=$\frac{1}{2}$×10×OC=14,
∴OC=$\frac{14}{5}$.
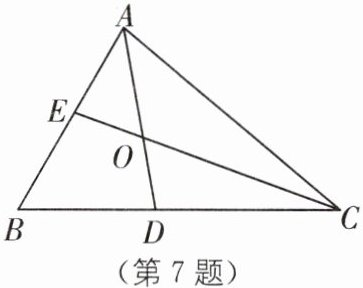
7. 截长补短 如图,在$\triangle ABC$中,$∠B= 60^{\circ }$,AD,CE 是$\triangle ABC$的角平分线,且交于点 O. 求证:$AC= AE+CD$.

答案:
如图,在AC上取点F,使AF=AE,连接OF.

∵AD平分∠BAC,
∴∠EAO=∠FAO.
在△AEO和△AFO中,$\left\{\begin{array}{l} AE=AF,\\ ∠EAO=∠FAO,\\ AO=AO,\end{array}\right. $
∴△AEO≌△AFO(SAS).
∴∠AOE=∠AOF.
∵AD,CE分别平分∠BAC,∠ACB,∠B=60°,
∴∠ECA+∠DAC=$\frac{1}{2}$(∠BAC+∠ACB)=$\frac{1}{2}$(180°-∠B)=60°,∠FCO=∠DCO,
∴∠AOE=∠COD=∠AOF=60°.
∴∠COF=180°-∠AOE-∠AOF=60°.
∴∠COD=∠COF.
在△FOC和△DOC中,$\left\{\begin{array}{l} ∠COF=∠COD,\\ CO=CO,\\ ∠FCO=∠DCO,\end{array}\right. $
∴△FOC≌△DOC(ASA).
∴DC=FC.
∴AC=AF+FC=AE+CD.
方法诠释 本题考查了全等三角形的判定和性质,三角形内角和定理,三角形外角的性质.利用截长补短的方法解题是关键.
如图,在AC上取点F,使AF=AE,连接OF.

∵AD平分∠BAC,
∴∠EAO=∠FAO.
在△AEO和△AFO中,$\left\{\begin{array}{l} AE=AF,\\ ∠EAO=∠FAO,\\ AO=AO,\end{array}\right. $
∴△AEO≌△AFO(SAS).
∴∠AOE=∠AOF.
∵AD,CE分别平分∠BAC,∠ACB,∠B=60°,
∴∠ECA+∠DAC=$\frac{1}{2}$(∠BAC+∠ACB)=$\frac{1}{2}$(180°-∠B)=60°,∠FCO=∠DCO,
∴∠AOE=∠COD=∠AOF=60°.
∴∠COF=180°-∠AOE-∠AOF=60°.
∴∠COD=∠COF.
在△FOC和△DOC中,$\left\{\begin{array}{l} ∠COF=∠COD,\\ CO=CO,\\ ∠FCO=∠DCO,\end{array}\right. $
∴△FOC≌△DOC(ASA).
∴DC=FC.
∴AC=AF+FC=AE+CD.
方法诠释 本题考查了全等三角形的判定和性质,三角形内角和定理,三角形外角的性质.利用截长补短的方法解题是关键.
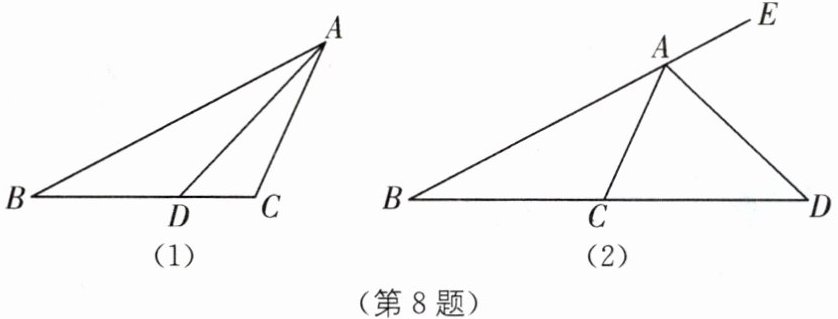
8. (2025·湖北宜昌期中)如图,在$\triangle ABC$中,AD 是角平分线. 求证:$S_{\triangle ABD}:S_{\triangle ACD}= AB:AC$.
(1)在图(1)中完成上面的证明过程;
(2)在图(2)中,AD 是$\triangle ABC$外角平分线,如果$AB= 10,AC= 4,BC= 7$,求 BD 的长.
(1)在图(1)中完成上面的证明过程;
(2)在图(2)中,AD 是$\triangle ABC$外角平分线,如果$AB= 10,AC= 4,BC= 7$,求 BD 的长.

答案:
(1)如图
(1),过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,
∴DE=DF,
∴$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}$=$\frac{\frac{1}{2}AB·DE}{\frac{1}{2}AC·DF}$=$\frac{AB}{AC}$.

(2)如图
(2),过点D作DM⊥AE于点M,DN⊥AC于点N.
∵AD平分∠EAC,
∴DM=DN,
∴$\frac{S_{\triangle ABD}}{S_{\triangle ADC}}$=$\frac{\frac{1}{2}AB·DM}{\frac{1}{2}AC·DN}$=$\frac{BD}{CD}$,
∵$\frac{AB}{AC}$=$\frac{BD}{CD}$=$\frac{10}{4}$=$\frac{5}{2}$,
∴$\frac{BD}{BC}$=$\frac{5}{3}$.
∵BC=7,
∴BD=$\frac{35}{3}$.
(1)如图
(1),过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,
∴DE=DF,
∴$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}$=$\frac{\frac{1}{2}AB·DE}{\frac{1}{2}AC·DF}$=$\frac{AB}{AC}$.

(2)如图
(2),过点D作DM⊥AE于点M,DN⊥AC于点N.
∵AD平分∠EAC,
∴DM=DN,
∴$\frac{S_{\triangle ABD}}{S_{\triangle ADC}}$=$\frac{\frac{1}{2}AB·DM}{\frac{1}{2}AC·DN}$=$\frac{BD}{CD}$,
∵$\frac{AB}{AC}$=$\frac{BD}{CD}$=$\frac{10}{4}$=$\frac{5}{2}$,
∴$\frac{BD}{BC}$=$\frac{5}{3}$.
∵BC=7,
∴BD=$\frac{35}{3}$.
查看更多完整答案,请扫码查看


