《2025年实验班提优训练八年级数学上册人教版》

12. 设 $ n $ 为某一自然数,代入代数式 $ n^{3}-n $ 计算其值时,四个学生算出了下列四个结果,其中正确的结果是(D).
A.521
B.1413
C.3721
D.1716

答案： D [解析]由题意可知原式$=n(n-1)(n+1)$,$\therefore n^{3}-n$为三个连续的正整数的积,$\therefore n^{3}-n$可写成三个连续自然数的积,其中一个因数必为偶数,$\therefore n^{3}-n$是一个偶数.故选D.

13. (2025·西安碑林区一模)分解因式:$ a x^{2}-4 a y^{2}= $____$a(x+2y)(x-2y)$.

答案： $a(x+2y)(x-2y)$ [解析]$ax^{2}-4ay^{2}=a(x^{2}-4y^{2})=a(x+2y)(x-2y)$.

14. 计算:$ 785^{2}-285^{2}= $535000.

答案： 535000 [解析]$785^{2}-285^{2}=(785+285)×(785-285)=1070×500=535000$.

15. (2025·河南南阳期中)如图(1)是一个棱长为 $ a $ 的正方体中挖去一个棱长为 $ b $ 的小正方体 $ (a＞b) $,将剩余部分进行切割得到如图(2)所示的三个长方体.通过计算剩余部分的体积,可对多项式 $ a^{3}-b^{3} $ 进行因式分解,即 $ a^{3}-b^{3}= $____.

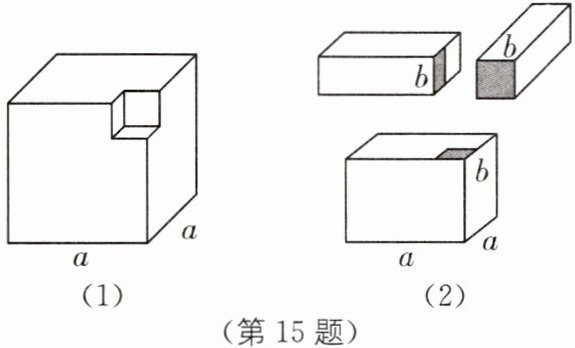
$(a-b)(a^{2}+ab+b^{2})$

答案： $(a-b)(a^{2}+ab+b^{2})$ [解析]根据题意可得图
(1)的体积为$a^{3}-b^{3}$,图
(2)体积为$a^{2}(a-b)+ab(a-b)+b^{2}(a-b)=(a-b)(a^{2}+ab+b^{2})$.$\because$图
(1)的体积=图
(2)的体积,$\therefore a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$.
思路引导 本题考查了因式分解的应用以及立方差公式,根据正方体和长方体的体积公式及体积关系,正确表示出三块长方体的体积之和,即可求解.

16. 多项式 $ 4 a^{2}-9 b^{n} $ (其中 $ n $ 是小于 10 的自然数,$ b \neq 0 $)可以分解因式,则 $ n $ 能取的值共有5种.

答案： 5 [解析]多项式$4a^{2}-9b^{n}$(其中n是小于10的自然数,$b\neq0$)可以分解因式,则n能取的值为0,2,4,6,8,共5种.

17. 将下列各式因式分解:
(1)$ (a-b)(3 a+b)^{2}+(a+3 b)^{2}(b-a) $;
(2)$ \left(4 x^{2}-9 y^{2}\right)(3 y-2 x)+9(2 x+3 y) $.

答案：
(1)原式$=(a-b)(3a+b)^{2}-(a+3b)^{2}(a-b)$$=(a-b)[(3a+b)^{2}-(a+3b)^{2}]$$=(a-b)(3a+b-a-3b)(3a+b+a+3b)$$=(a-b)(2a-2b)(4a+4b)$$=8(a-b)^{2}(a+b)$.
(2)原式$=(2x-3y)(2x+3y)(3y-2x)+9(2x+3y)$$=(2x+3y)[9-(2x-3y)^{2}]$$=(2x+3y)(3-2x+3y)(3+2x-3y)$.

18. 利用因式分解计算:$ 1-2^{2}+3^{2}-4^{2}+5^{2}-6^{2}+…+99^{2}-100^{2}+101^{2} $.

答案： $1-2^{2}+3^{2}-4^{2}+5^{2}-6^{2}+\cdots+99^{2}-100^{2}+101^{2}$$=1+3^{2}-2^{2}+5^{2}-4^{2}+\cdots+101^{2}-100^{2}$$=1+(3+2)×(3-2)+(5+4)×(5-4)+\cdots+(101+100)×(101-100)$$=1+(3+2)+(5+4)+\cdots+(101+100)$$=\frac{(1+101)×101}{2}=5151$.

19. (2025·江苏南通期中)在分解因式时,小彬和小颖对同一道题产生了分歧,下面是他们的解答过程,请认真阅读并完成相应的任务.
题目:将 $ (2 x+y)^{2}-(x+2 y)^{2} $ 分解因式
小彬的解法:
$ (2 x+y)^{2}-(x+2 y)^{2} $
$ =\left(4 x^{2}+4 x y+y^{2}\right)-\left(x^{2}+4 x y+4 y^{2}\right) $
…… 第1步
$ =3 x^{2}-3 y^{2} $
…… 第2步
$ =3(x+y)(x-y) $
…… 第3步
小颖的解法:
$ (2 x+y)^{2}-(x+2 y)^{2} $
$ =(2 x+y+x+2 y) \cdot(2 x+y-x+2 y) $
…… 第1步
$ =(3 x+3 y)(x+3 y) $
…… 第2步
$ =3(x+y)(x+3 y) $
…… 第3步
任务:
(1)老师批阅后发现两人中只有一人的解答结果正确,则解答正确的同学是小彬;
(2)老师认为两名同学的解答过程都有道理:小彬同学的第 1 步是运用了完全平方公式;小颖同学的第 1 步是运用了平方差公式;
(3)请你按照做错同学的思路,写出正确的解答过程.
$(2x+y)^{2}-(x+2y)^{2}$$=(2x+y+x+2y)(2x+y-x-2y)$$=(3x+3y)(x-y)=3(x+y)(x-y)$.

答案：
(1)小彬
(2)完全平方 平方差
(3)$(2x+y)^{2}-(x+2y)^{2}$$=(2x+y+x+2y)(2x+y-x-2y)$$=(3x+3y)(x-y)=3(x+y)(x-y)$.