第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
【例】(第二十二届“华杯赛”决赛)直线 $ a $ 平行于直线 $ b $,$ a $ 上有 $ 5 $ 个点 $ A _ { 1 } , A _ { 2 } , \cdots , A _ { 5 } $,$ b $ 上有 $ 5 $ 个点 $ B _ { 1 } , B _ { 2 } , \cdots , B _ { 5 } $,连接线段 $ A _ { i } B _ { j } ( i , j = 1 , 2 , 3 , 4 , 5 ) $ 所得到的图形中,三角形最多有多少个?
答案:
100+400+400+100=1000(个)
答:三角形最多有$1000$个。
答:三角形最多有$1000$个。
1. (全国初中数学竞赛初赛)如图,点 $ D $,$ E $ 分别在 $ \triangle A B C $ 的边 $ A B $,$ A C $ 上,$ B E $,$ C D $ 相交于点 $ F $,设四边形 $ E A D F $,$ \triangle B D F $,$ \triangle B C F $,$ \triangle C E F $ 的面积分别为 $ S _ { 1 } $,$ S _ { 2 } $,$ S _ { 3 } $,$ S _ { 4 } $,则 $ S _ { 1 } S _ { 3 } $ 与 $ S _ { 2 } S _ { 4 } $ 的大小关系为(
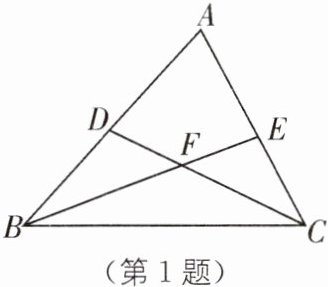
A.$ S _ { 1 } S _ { 3 } < S _ { 2 } S _ { 4 } $
B.$ S _ { 1 } S _ { 3 } = S _ { 2 } S _ { 4 } $
C.$ S _ { 1 } S _ { 3 } > S _ { 2 } S _ { 4 } $
D.不能确定
C
)。
A.$ S _ { 1 } S _ { 3 } < S _ { 2 } S _ { 4 } $
B.$ S _ { 1 } S _ { 3 } = S _ { 2 } S _ { 4 } $
C.$ S _ { 1 } S _ { 3 } > S _ { 2 } S _ { 4 } $
D.不能确定
答案:
1.C [解析]连接DE,设$S_{\triangle DEF}=S_{1}^{'}$,则$\frac{S_{1}^{'}}{S_{2}}=\frac{EF}{BF}=\frac{S_{4}}{S_{3}}$,从而有$S_{1}^{'}S_{3}=S_{2}S_{4}$.$\because S_{1}>S_{1}^{'}$,$\therefore S_{1}S_{3}>S_{2}S_{4}$.故选C.
2. (全国初中数学竞赛初赛)如图,$ P $ 为 $ \triangle A B C $ 内一点,$ \angle B A C = 70 ^ { \circ } $,$ \angle B P C = 120 ^ { \circ } $,$ B D $ 是 $ \angle A B P $ 的平分线,$ C E $ 是 $ \angle A C P $ 的平分线,$ B D $ 与 $ C E $ 交于点 $ F $,则 $ \angle B F C $ 等于( )。
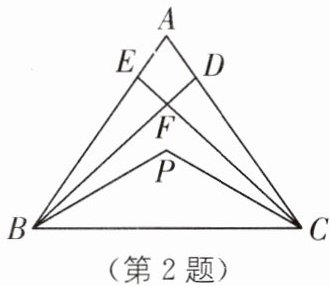
A.$ 85 ^ { \circ } $
B.$ 90 ^ { \circ } $
C.$ 95 ^ { \circ } $
D.$ 100 ^ { \circ } $

A.$ 85 ^ { \circ } $
B.$ 90 ^ { \circ } $
C.$ 95 ^ { \circ } $
D.$ 100 ^ { \circ } $
答案:
2.C [解析]如图,延长BP交AC于点Q,

则$\angle BPC=\angle ACP+\angle BQC$.
$\because \angle BQC=\angle A+\angle ABQ$,
$\therefore \angle BPC=\angle A+\angle ACP+\angle ABQ$①.
又$\angle BFC=\angle ACE+\angle BDC$,$\angle BDC=\angle A+\angle ABD$,
$\therefore \angle BFC=\angle A+\angle ACE+\angle ABD$②.
又$\angle ACP=2\angle ACE$,$\angle ABQ=2\angle ABD$,结合①②两式可得$\angle BPC=\angle A+2\angle ACE+2\angle ABD=2(\angle A+ \angle ACE+\angle ABD)-\angle A=2\angle BFC-\angle A$,$\therefore \angle BFC= \frac{1}{2}(\angle BPC+\angle A)=\frac{1}{2}×(120^{\circ}+70^{\circ})=95^{\circ}$.故选C.
2.C [解析]如图,延长BP交AC于点Q,

则$\angle BPC=\angle ACP+\angle BQC$.
$\because \angle BQC=\angle A+\angle ABQ$,
$\therefore \angle BPC=\angle A+\angle ACP+\angle ABQ$①.
又$\angle BFC=\angle ACE+\angle BDC$,$\angle BDC=\angle A+\angle ABD$,
$\therefore \angle BFC=\angle A+\angle ACE+\angle ABD$②.
又$\angle ACP=2\angle ACE$,$\angle ABQ=2\angle ABD$,结合①②两式可得$\angle BPC=\angle A+2\angle ACE+2\angle ABD=2(\angle A+ \angle ACE+\angle ABD)-\angle A=2\angle BFC-\angle A$,$\therefore \angle BFC= \frac{1}{2}(\angle BPC+\angle A)=\frac{1}{2}×(120^{\circ}+70^{\circ})=95^{\circ}$.故选C.
3. (全国初中数学竞赛初赛)已知 $ \triangle A B C $ 的三个内角满足 $ \angle A < \angle B < \angle C < 100 ^ { \circ } $,用 $ \theta $ 表示 $ 100 ^ { \circ } - \angle C $,$ \angle C - \angle B $,$ \angle B - \angle A $ 中的最小值,则 $ \theta $ 的最大值为____
20°
。
答案:
3.$20^{\circ}$ [解析]$\because \theta$表示$100^{\circ}-\angle C$,$\angle C-\angle B$,$\angle B-\angle A$中的最小值,$\therefore \theta \leq 100^{\circ}-\angle C$,$\theta \leq \angle C-\angle B$,$\theta \leq \angle B- \angle A$,$\therefore 6\theta \leq 3(100^{\circ}-\angle C)+2(\angle C-\angle B)+(\angle B- \angle A)$,$\therefore 6\theta \leq 300^{\circ}-(\angle A+\angle B+\angle C)=120^{\circ}$,$\therefore \theta \leq 20^{\circ}$.又当$100^{\circ}-\angle C=\angle C-\angle B=\angle B-\angle A=20^{\circ}$,即$\angle C=80^{\circ}$,$\angle B=60^{\circ}$,$\angle A=40^{\circ}$时,满足条件,故$\theta$可取到$20^{\circ}$.因此,$\theta$的最大值为$20^{\circ}$.
查看更多完整答案,请扫码查看


