第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
16. (2025·安徽芜湖期末)(1)填空:$ (x - 1)(x + 1) = $
(2)猜想:$ (x - 1)(x^{n} + x^{n - 1} + … + x + 1) = $
(3)求$ 2^{2024} + 2^{2023} + 2^{2022} + 2^{2021} + … + 2^{2} + 2 + 1 $的值。
$x^{2}-1$
,$ (x - 1)(x^{2} + x + 1) = $$x^{3}-1$
,$ (x - 1)(x^{3} + x^{2} + x + 1) = $$x^{4}-1$
;(2)猜想:$ (x - 1)(x^{n} + x^{n - 1} + … + x + 1) = $
$x^{n+1}-1$
($ n $为正整数);(3)求$ 2^{2024} + 2^{2023} + 2^{2022} + 2^{2021} + … + 2^{2} + 2 + 1 $的值。
$2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1$$=(2-1)(2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1)$$=2^{2025}-1.$
答案:
(1)$x^{2}-1$$x^{3}-1$$x^{4}-1$[解析]$(x-1)(x+1)=$$x^{2}+x-x-1=x^{2}-1;$$(x-1)(x^{2}+x+1)=x^{3}+x^{2}+x-x^{2}-x-1=x^{3}-1;$$(x-1)(x^{3}+x^{2}+x+1)=x^{4}+x^{3}+x^{2}+x-x^{3}-x^{2}-x-1=x^{4}-1.$
(2)$x^{n+1}-1$
(3)$2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1$$=(2-1)(2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1)$$=2^{2025}-1.$
(1)$x^{2}-1$$x^{3}-1$$x^{4}-1$[解析]$(x-1)(x+1)=$$x^{2}+x-x-1=x^{2}-1;$$(x-1)(x^{2}+x+1)=x^{3}+x^{2}+x-x^{2}-x-1=x^{3}-1;$$(x-1)(x^{3}+x^{2}+x+1)=x^{4}+x^{3}+x^{2}+x-x^{3}-x^{2}-x-1=x^{4}-1.$
(2)$x^{n+1}-1$
(3)$2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1$$=(2-1)(2^{2024}+2^{2023}+2^{2022}+2^{2021}+... +2^{2}+2+1)$$=2^{2025}-1.$
17. 数形结合思想(2025·湖北黄冈期末)数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题。如图(1)是一个边长为$ a + b $的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为$ a 和 b $,阴影部分的面积所揭示的乘法公式是$ (a + b)^{2} = a^{2} + 2ab + b^{2} $。
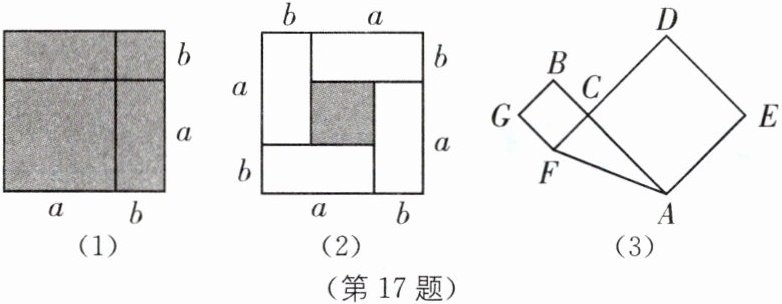
(1)用4个全等的长和宽分别为$ a $,$ b $的长方形拼摆成一个如图(2)的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式$ (a + b)^{2} $,$ (a - b)^{2} $,$ ab $之间的等量关系;
(2)如图(3),$ C 是线段 AB $上的一点,分别以$ AC $,$ BC 为边向两边作正方形 ACDE 和 BCFG $,若$ AB = 9 $,两正方形的面积和为41,求$ \triangle AFC $的面积;
(3)若$ (2024 - m)(2025 - m) = 6 $,则$ (2024 - m)^{2} + (2025 - m)^{2} = $____。(直接写出结果)

(1)用4个全等的长和宽分别为$ a $,$ b $的长方形拼摆成一个如图(2)的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式$ (a + b)^{2} $,$ (a - b)^{2} $,$ ab $之间的等量关系;
(2)如图(3),$ C 是线段 AB $上的一点,分别以$ AC $,$ BC 为边向两边作正方形 ACDE 和 BCFG $,若$ AB = 9 $,两正方形的面积和为41,求$ \triangle AFC $的面积;
(3)若$ (2024 - m)(2025 - m) = 6 $,则$ (2024 - m)^{2} + (2025 - m)^{2} = $____。(直接写出结果)
答案:
(1)由题意,题图
(2)中阴影部分是边长为$(a-b)$的正方形,其面积为$(a-b)^{2}$或$(a+b)^{2}-4ab,$$\therefore (a-b)^{2}=(a+b)^{2}-4ab.$
(2)设$AC=a,BC=CF=b,$$\because AB=9$,两正方形的面积和为 41,$\therefore a+b=9,a^{2}+b^{2}=41.$由$(a+b)^{2}=a^{2}+b^{2}+2ab$得$9^{2}=41+2ab,$解得$ab=20,\therefore S_{\triangle AFC}=\frac {1}{2}ab=\frac {1}{2}×20=10.$
(3)13 [解析]设$a=2024-m,b=2025-m$,则$a-b=1$,由$(2024-m)(2025-m)=6$得$ab=6,$由$(a-b)^{2}=a^{2}+b^{2}-2ab$得$1^{2}=a^{2}+b^{2}-2×6,$$\therefore a^{2}+b^{2}=13$,即$(2024-m)^{2}+(2025-m)^{2}=13.$
(1)由题意,题图
(2)中阴影部分是边长为$(a-b)$的正方形,其面积为$(a-b)^{2}$或$(a+b)^{2}-4ab,$$\therefore (a-b)^{2}=(a+b)^{2}-4ab.$
(2)设$AC=a,BC=CF=b,$$\because AB=9$,两正方形的面积和为 41,$\therefore a+b=9,a^{2}+b^{2}=41.$由$(a+b)^{2}=a^{2}+b^{2}+2ab$得$9^{2}=41+2ab,$解得$ab=20,\therefore S_{\triangle AFC}=\frac {1}{2}ab=\frac {1}{2}×20=10.$
(3)13 [解析]设$a=2024-m,b=2025-m$,则$a-b=1$,由$(2024-m)(2025-m)=6$得$ab=6,$由$(a-b)^{2}=a^{2}+b^{2}-2ab$得$1^{2}=a^{2}+b^{2}-2×6,$$\therefore a^{2}+b^{2}=13$,即$(2024-m)^{2}+(2025-m)^{2}=13.$
18. 一题多问(2025·北京东城区期末)如图,有正方形$ A $,$ B $,现将$ B 放在 A $的内部得图(1),将$ A $,$ B $并列放置后构造新的正方形得图(2),若图(1),图(2)中阴影部分的面积分别为4,30。证明:
(1)正方形$ A 和 B $的面积和是34;
(2)图(2)中新的正方形的面积是64;
(3)正方形$ A 和 B $的面积差是16;
(4)正方形$ A $的边长是5。
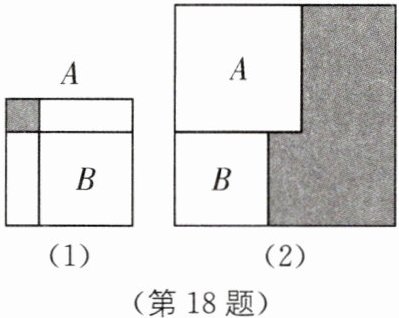
(1)正方形$ A 和 B $的面积和是34;
(2)图(2)中新的正方形的面积是64;
(3)正方形$ A 和 B $的面积差是16;
(4)正方形$ A $的边长是5。

答案:
(1)设正方形 A 的边长为 a,正方形 B 的边长为 b,图
(1)的阴影部分是边长为$a-b$的正方形,因此面积为$(a-b)^{2},$图
(2)的阴影部分是边长为$a+b$的大正方形与边长为 a,边长为 b 的两个正方形的面积差,即$(a+b)^{2}-a^{2}-b^{2},$
∵图
(1),图
(2)中阴影部分的面积分别为 4,30.$\therefore (a-b)^{2}=4,(a+b)^{2}-a^{2}-b^{2}=30$,即$ab=15,$$\therefore a^{2}-2ab+b^{2}=4$,即$a^{2}+b^{2}=4+2ab=4+30=34$,故正方形 A 和 B 的面积和是 34.
(2)由
(1)可得$(a+b)^{2}=(a-b)^{2}+4ab=4+60=64,$故图
(2)中新的正方形的面积是 64.
(3)$\because (a-b)^{2}=4,(a+b)^{2}=64,a>b>0,$$\therefore a-b=2,a+b=8,\therefore a=5,b=3,$$\therefore a^{2}-b^{2}=25-9=16,$即正方形 A 与正方形 B 的面积差为 16.
(4)由
(3)得正方形 A 的边长为 5.
(1)设正方形 A 的边长为 a,正方形 B 的边长为 b,图
(1)的阴影部分是边长为$a-b$的正方形,因此面积为$(a-b)^{2},$图
(2)的阴影部分是边长为$a+b$的大正方形与边长为 a,边长为 b 的两个正方形的面积差,即$(a+b)^{2}-a^{2}-b^{2},$
∵图
(1),图
(2)中阴影部分的面积分别为 4,30.$\therefore (a-b)^{2}=4,(a+b)^{2}-a^{2}-b^{2}=30$,即$ab=15,$$\therefore a^{2}-2ab+b^{2}=4$,即$a^{2}+b^{2}=4+2ab=4+30=34$,故正方形 A 和 B 的面积和是 34.
(2)由
(1)可得$(a+b)^{2}=(a-b)^{2}+4ab=4+60=64,$故图
(2)中新的正方形的面积是 64.
(3)$\because (a-b)^{2}=4,(a+b)^{2}=64,a>b>0,$$\therefore a-b=2,a+b=8,\therefore a=5,b=3,$$\therefore a^{2}-b^{2}=25-9=16,$即正方形 A 与正方形 B 的面积差为 16.
(4)由
(3)得正方形 A 的边长为 5.
查看更多完整答案,请扫码查看


