《2025年实验班提优训练八年级数学上册人教版》

1. (2025·山东济宁金乡期末)如图,已知$∠A=60^{\circ },∠B=40^{\circ },∠C=30^{\circ }$,则$∠D+∠E$等于(C).

A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$

答案： C [解析]连接 BC,如图所示,
∵∠A=60°,∠ABE=40°,∠ACD=30°,
∴∠1+∠2=180°-∠A-∠ABE-∠ACD=180°-60°-40°-30°=50°.
∵∠D+∠E=∠1+∠2,
∴∠D+∠E=50°.故选 C.

变式1.1 小慧一笔画成了如图所示的图形,若$∠A=60^{\circ }$,则$∠B+∠C+∠D+∠E$的度数为( ).


A.$180^{\circ }$
B.$240^{\circ }$
C.$270^{\circ }$
D.$300^{\circ }$

答案：
B [解析]如图,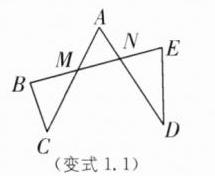
在△BCM中,∠B+∠C+∠BMC=180°,
∴∠BMC=180°-(∠B+∠C).
∵∠AMN=∠BMC,
∴∠AMN=180°-(∠B+∠C).
在△DEN中,∠D+∠E+∠DNE=180°,
∴∠DNE=180°-(∠D+∠E).
∵∠ANM=∠DNE,
∴∠ANM=180°-(∠D+∠E).
在△AMN中,∠A+∠AMN+∠ANM=180°,
∴∠A+180°-(∠B+∠C)+180°-(∠D+∠E)=180°.
∴∠B+∠C+∠D+∠E=∠A+180°.
∵∠A=60°,
∴∠B+∠C+∠D+∠E=240°.故选 B.

2. 在$△ABC$中,BE为$△ABC$的高,$∠A=50^{\circ },∠CBE=20^{\circ }$,则$∠ABC=$20或60$^{\circ }$.

答案： 20或60 [解析]依题意画出图形,如图所示.
∵BE为△ABC的高,
∴∠AEB=90°.
在△ABE中,∠AEB=90°,∠A=50°,
∴∠ABE=180°-∠AEB-∠A=180°-90°-50°=40°.
当△ABC为钝角三角形时,∠ABC=∠ABE-∠CBE=40°-20°=20°;
当△ABC为锐角三角形时,∠ABC=∠ABE+∠CBE=40°+20°=60°.
∴∠ABC=20°或60°.

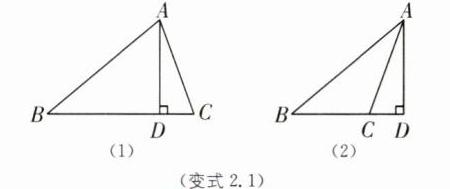
变式2.1 在$△ABC$中,AD为边BC上的高,$∠BAD= 50^{\circ },∠CAD= 20^{\circ }$,则$∠BAC$的度数为____.

答案：
70°或30° [解析]如图
(1),∠BAC=∠BAD+∠CAD=50°+20°=70°.
如图
(2),∠BAC=∠BAD-∠CAD=50°-20°=30°.

变式2.2 当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为$126^{\circ }$,那么这个“梦想三角形”的最小内角的度数为12°或13.5°.

答案： 12°或13.5° [解析]①126°÷3=42°,180°-126°-42°=12°,则这个"梦想三角形"的最小内角的度数为12°;
②设这个"梦想三角形"的其他两个内角的度数分别为3x,x,则3x+x+126°=180°,解得x=13.5°,则这个"梦想三角形"的最小内角的度数为13.5°.

变式2.3 在$△ABC$中,$∠A= 50^{\circ }$,BD,CE是它的两条高,直线BD,CE交于点F,则$∠DFE= $____.

答案：
130°或50° [解析]当△ABC为锐角三角形时,如图
(1),
∵∠A=50°,BD,CE是它的两条高,
∴∠ADF=∠CDF=∠AEF=90°,
∴∠ACE=90°-50°=40°,
∴∠DFE=130°;
当△ABC为钝角三角形时,如图
(2)
(3),
∵∠A=50°,BD是它的高,
∴∠ABD=40°.
∵CE是△ABC的高,
∴∠DFE=50°.
→常见的8字型
综上所述:∠DFE=130°或∠DFE=50°.

(1)$∠ABO$的度数为30$^{\circ },△AOB$不是(填“是”或“不是”)“智慧三角形”；
(2)若$∠OAC= 20^{\circ }$,求证:$△AOC$为“智慧三角形”；
∵∠AOC=60°,∠OAC=20°,
∴∠AOC=3∠OAC,∠ACO=180°-60°-20°=100°,
∴△AOC为"智慧三角形".
(3)当$△ABC$为“智慧三角形”时,求$∠OAC$的度数.(直接写出答案)
80°或52.5°或97.5°或112.5°

答案：
(1)30 不是 [解析]
∵AB⊥OM,
∴∠OAB=90°,
∴∠ABO=90°-∠MON=30°,
∴△AOB为直角三角形,不是"智慧三角形".
(2)
∵∠AOC=60°,∠OAC=20°,
∴∠AOC=3∠OAC,∠ACO=180°-60°-20°=100°,
∴△AOC为"智慧三角形".
(3)80°或52.5°或97.5°或112.5°

3. (2025·山东济南章丘区期末)如图,在$△AOB$中,$AO_{1},BO_{1}$分别平分$∠OAB,∠OBA,AO_{2},BO_{2}$分别平分$∠OAO_{1},∠OBO_{1}$,若$∠O=60^{\circ }$,则$∠O_{2}=$A.
A.$90^{\circ }$
B.$100^{\circ }$
C.$110^{\circ }$
D.$120^{\circ }$

答案： A [解析]
∵∠O+∠OAB+∠OBA=180°,
∴∠OAB+∠OBA=180°-∠O=180°-60°=120°.
∵AO₁,BO₁分别平分∠OAB,∠OBA,
∴∠O₁AB=∠O₁AO=$\frac{1}{2}$∠OAB,∠O₁BA=∠O₁BO=$\frac{1}{2}$∠OBA.
∵AO₂,BO₂分别平分∠OAO₁,∠OBO₁,
∴∠O₂AO₁=$\frac{1}{2}$∠O₁AO=$\frac{1}{4}$∠OAB,∠O₂BO₁=$\frac{1}{2}$∠O₁BO=$\frac{1}{4}$∠OAB,
∴∠O₂AB+∠O₂BA=$\frac{3}{4}$∠OAB+$\frac{3}{4}$∠OBA=$\frac{3}{4}$(∠OAB+∠OBA)=$\frac{3}{4}$×120°=90°,
∴∠O₂=180°-(∠O₂AB+∠O₂BA)=180°-90°=90°.
故选 A.