《2025年实验班提优训练八年级数学上册人教版》

16. (2025·上海静安区期末)已知 $(a - b)^{2}= 15$,$ab = -\frac{5}{2}$,求 $a^{4}+b^{4}$ 的值。

答案： 16.
∵(a−b)²=15,
∴a²−2ab+b²=15.
∵ab=−5/2,
∴a²+b²=15−5=10，
∴a⁴+b⁴=(a²+b²)²−2a²b²=10²−2×(−5/2)²=100−12.5=87.5.

17. (2025·上海闵行区期中)(1)已知 $a + b = 3$,$ab = 2$,则 $a^{2}+b^{2}=$5,$(a - b)^{2}=$1；
(2)已知 $a + b + c = 6$,$ab + bc + ac = 11$,求 $a^{2}+b^{2}+c^{2}$ 的值。
由条件可知(a+b+c)²=36，(a+b)²+2(a+b)c+c²=36，a²+2ab+b²+2ac+2bc+c²=36，a²+b²+c²+2ab+2ac+2bc=36，∵2ab+2bc+2ac=22,∴a²+b²+c²+22=36，∴a²+b²+c²=14.

答案： 17.
(1)5 1 [解析]
∵a+b=3,ab=2，
∴a²+b²=(a+b)²−2ab=3²−2×2=9−4=5，(a−b)²=a²+b²−2ab=5−2×2=1.
(2)由条件可知(a+b+c)²=36，(a+b)²+2(a+b)c+c²=36，a²+2ab+b²+2ac+2bc+c²=36，a²+b²+c²+2ab+2ac+2bc=36，
∵2ab+2bc+2ac=22,
∴a²+b²+c²+22=36，
∴a²+b²+c²=14.

18. 中考新考法 操作探究 (2025·广东汕头潮阳区期末)
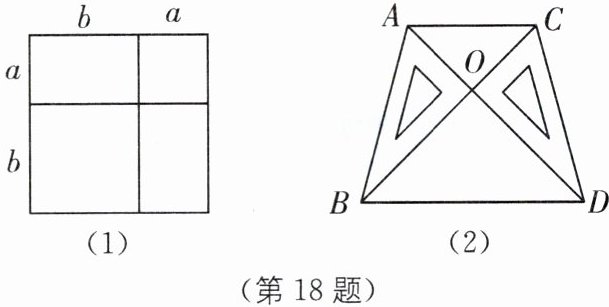
[阅读理解]我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式。例如图(1)可以得到 $(a + b)^{2}= a^{2}+2ab + b^{2}$,基于此,请解答下列问题：
[类比应用]
(1)①若 $xy = 8$,$x + y = 6$,则 $x^{2}+y^{2}$ 的值为20；②若 $x(5 - x)= 6$,则 $x^{2}+(5 - x)^{2}= $13；
[迁移应用]
(2)两块完全相同的特制直角三角板 $(\angle AOB= \angle COD = 90^{\circ})$ 如图(2)所示放置,其中 $A$,$O$,$D$ 在一条直线上,连接 $AC$,$BD$,若 $AD = 14$,$S_{\triangle AOC}+S_{\triangle BOD}= 54$,求一块三角板的面积。

设三角板的两条直角边AO=m,BO=n，则一块三角板的面积为1/2mn，∴m+n=14,1/2(m²+n²)=54，即m²+n²=108，∴2mn=(m+n)²−(m²+n²)=14²−108=88，∴mn=44,∴1/2mn=1/2×44=22，∴一块三角板的面积是22.

答案： 18.
(1)①20 [解析]由题意可知，x²+y²=(x+y)²−2xy，
∵xy=8,x+y=6,
∴x²+y²=6²−2×8=20.
②13 [解析]令a=x,b=5−x,
∴a+b=5,ab=6，
∴x²+(5−x)²=a²+b²=(a+b)²−2ab=5²−2×6=13.
(2)设三角板的两条直角边AO=m,BO=n，则一块三角板的面积为1/2mn，
∴m+n=14,1/2(m²+n²)=54，即m²+n²=108，
∴2mn=(m+n)²−(m²+n²)=14²−108=88，
∴mn=44,
∴1/2mn=1/2×44=22，
∴一块三角板的面积是22.

19. (2025·河南南阳期末)对于任意实数 $m$,$n$,我们规定：$F(m,n)= m^{2}+n^{2}$,$H(m,n)= mn$,例如：$F(1,2)= 1^{2}+2^{2}= 5$,$H(3,4)= 3×4 = 12$。
(1)填空：
①$F(-1,3)=$10；
②若 $H(2,x)= -6$,则 $x=$-3；
③若 $F(a,b)= H(a,2b)$,则 $a - b$=0。(填“$＞$”“$＜$”或“$=$”)
(2)若 $x + 2y = 5$,且 $F(2x + 3y,2x - 3y)-H(7,x^{2}+2y^{2})= 13$,求 $xy$ 与 $(x - 2y)^{2}$ 的值。
∵F(2x+3y,2x−3y)−H(7,x²+2y²)=13，∴(2x+3y)²+(2x−3y)²−7(x²+2y²)=13，即x²+4y²=13.∵x+2y=5,∴x²+4y²+4xy=25，∴xy=3,∴(x−2y)²=x²+4y²−4xy=1.

答案： 19.
(1)①10 ②−3
③= [解析]若F(a,b)=H(a,2b)，则a²+b²=2ab，则(a−b)²=0，故a−b=0.
(2)
∵F(2x+3y,2x−3y)−H(7,x²+2y²)=13，
∴(2x+3y)²+(2x−3y)²−7(x²+2y²)=13，即x²+4y²=13.
∵x+2y=5,
∴x²+4y²+4xy=25，
∴xy=3,
∴(x−2y)²=x²+4y²−4xy=1.

20. 数形结合思想 (2025·广东湛江期末)把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法。我们在学习“从面积到乘法公式”时,曾用两种不同的方法计算同一个图形的面积,探索了完全平方公式：$(a + b)^{2}= a^{2}+2ab + b^{2}$(如图(1))。

(1)观察图(2),请你写出 $(a + b)^{2}$,$(a - b)^{2}$,$ab$ 之间的等量关系：$(a+b)²=(a−b)²+4ab$；
拓展应用：根据(1)中的等量关系及课本所学的完全平方公式知识,解决如下问题：
(2)若 $x + y = 4$,$xy= \frac{7}{4}$,且 $x ＞ y$,求 $x - y$ 的值；3
(3)若 $(2025 - m)^{2}+(m - 2024)^{2}= 7$,求 $(2025 - m)(m - 2024)$ 的值；-3
(4)如图(3),在 $\triangle BCE$ 中,$\angle BCE = 90^{\circ}$,$CE = 8$,点 $M$ 在边 $BC$ 上,$CM = 3$,在边 $CE$ 上取一点 $Q$,使 $BM = EQ$,分别以 $BC$,$CQ$ 为边在 $\triangle BCE$ 外部作正方形 $ABCD$ 和正方形 $COPQ$,连接 $BQ$,若 $\triangle BCQ$ 的面积等于 $\frac{21}{2}$,设 $BM = x(x ＞ 0)$,求正方形 $ABCD$ 和正方形 $COPQ$ 的面积和。79

答案： 20.
(1)(a+b)²=(a−b)²+4ab [解析]由图可知大正方形的面积等于4个长方形的面积加上小正方形的面积，
∴(a+b)²=(a−b)²+4ab.
(2)由
(1)可得(x−y)²=(x+y)²−4xy，
∴(x−y)²=(x+y)²−4xy=4²−4×7/4=9.
∵x＞y,
∴x−y=3.
(3)
∵(a+b)²=a²+2ab+b²，
∴2ab=(a+b)²−(a²+b²).
∵(2025−m)²+(m−2024)²=7，
∴2(2025−m)(m−2024)=(2025−m+m−2024)²−[(2025−m)²+(m−2024)²]=1−7=−6，
∴(2025−m)(m−2024)=−6/2=−3.
(4)设BM=x，则BM=EQ=x，
∵CM=3,CE=8，
∴CQ=CE−EQ=8−x,BC=BM+CM=3+x.
∵S△BCQ=1/2BC·CQ=21/2,
∴(8−x)(3+x)=21.令8−x=a,x+3=b,
∴a+b=11,ab=21，
∴正方形ABCD和正方形COPQ的面积和=a²+b²=(a+b)²−2ab=11²−2×21=121−42=79.