《2025年一遍过八年级数学上册北师大版》

1 [2025郑州金水区期末]杨老师在“双十一”期间买了一件毛衣,通过研究缝在衣服内部标签上的内容,得到了以下结论:
①毛衣的总质量为200g;
②毛衣的成分:绵羊毛、腈纶、锦纶、聚酯纤维;
③绵羊毛和腈纶的含量占20%,锦纶的含量是绵羊毛含量的5倍,聚酯纤维的含量比腈纶含量的2倍少1g。
请你求出这件毛衣中绵羊毛和腈纶的质量。

答案： 解：设这件毛衣中绵羊毛的质量为xg，腈纶的质量为yg，则锦纶的质量为5xg，聚酯纤维的质量为$(2y-1)g$，
根据题意，得$\left\{\begin{array}{l} x+y=200×20\% ,\\ x+y+5x+2y-1=200,\end{array}\right.$ 解得$\left\{\begin{array}{l} x=27,\\ y=13,\end{array}\right.$
所以这件毛衣中绵羊毛的质量为27g，腈纶的质量为13g。

2 [2025岳阳期末]你看过《一千零一夜》吗?有个故事中有一个绝妙的谜语:有一群鸽子,飞过一棵高高的树,一部分鸽子落在树上,其他的停在树下,一只落在树上的鸽子对树下的鸽子说:“倘若你们当中有一只飞上来,你们的数目就是我们总数的$\frac{1}{3}$;倘若我们中飞下去一只,我们的数目恰好和你们相同啦!”根据这段描述,请你算一算,有多少只鸽子在树上,多少只鸽子在树下。

答案： 解：设有x只鸽子在树上，有y只鸽子在树下，
由题意，得$\left\{\begin{array}{l} \frac {1}{3}(x+y)=y-1,\\ x-1=y+1,\end{array}\right.$ 解得$\left\{\begin{array}{l} x=7,\\ y=5,\end{array}\right.$
所以有7只鸽子在树上，有5只鸽子在树下。

3 [2025台州期末]两位同学设计一款填数游戏,根据如图所示信息解决问题。

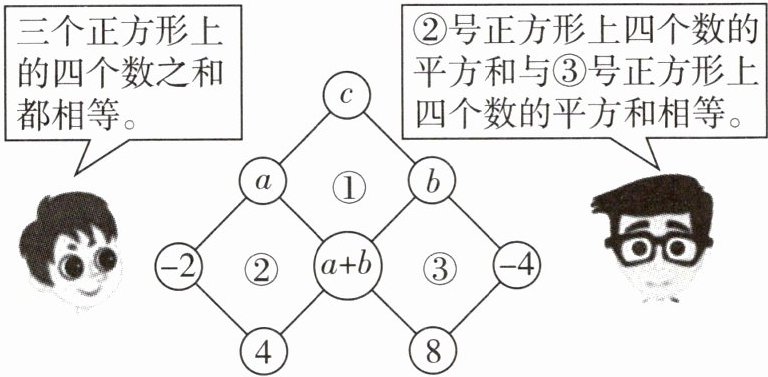
(1)求$a,b$之间的数量关系;
$a=$$b+2$
(2)求$c$的值。
$c=$$-12$

答案： 解：（1）根据题意，得$a-2+4=b-4+8$，
所以$a=b+2$。
（2）根据题意，得$(-2)^{2}+4^{2}+a^{2}=8^{2}+(-4)^{2}+b^{2}$，
所以$a^{2}=60+b^{2}$，
因为$a=b+2$，所以$(b+2)^{2}=60+b^{2}$，
解得$b=14$，所以$a=16$，
又因为$-2+4=c+b$，
所以$c=2-b=2-14=-12$。（先确定a，b之间的数量关系，然后得到b的值，进而得到a的值，最后求得c的值）

4 [2025湖州期末]已知$M,N两点在数轴上所表示的数分别为m,n$,且$m,n满足|m-10|+(n+2)^{2}= 0$。

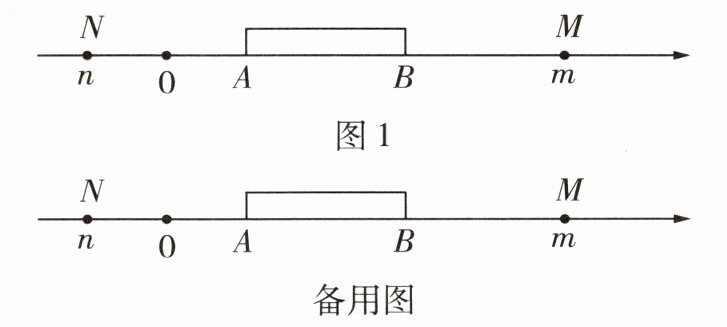
(1)填空:$m= $10,$n= $-2。
(2)问题探究:将一根木棒$AB$如图1所示放置在数轴上,将木棒沿数轴左右水平移动,当点$A移动到点B$时,点$B所对应的数为m$;当点$B移动到点A$时,点$A所对应的数为n$,由此可得这根木棒的长为4个单位。
(3)在(2)的条件下,现将木棒$AB$从某点处切断,切断后左边的木棒以每秒4个单位的速度往左移动,同时右边的木棒以每秒5个单位的速度往右移动,是否存在某一时刻,$M和N$刚好是两段木棒的中点?若存在,求出木棒切断处所表示的数;若不存在,请说明理由。

答案： 解：（1）10 -2
因为$|m-10|+(n+2)^{2}=0$，所以$m-10=0$，$n+2=0$，所以$m=10$，$n=-2$。
（2）4
由（1）知，$MN=10-(-2)=12$，根据题意，得$AB=\frac {1}{3}MN=4$，即这根木棒的长为4个单位。
（3）存在某一时刻，M和N刚好是两段木棒的中点。理由如下：
设木棒切断处所表示的数为x，两段木棒运动的时间为t秒，A表示的数为$-2+4=2$，B表示的数为$10-4=6$，
根据题意，得$\left\{\begin{array}{l} \frac {2-4t+x-4t}{2}=-2,\\ \frac {x+5t+6+5t}{2}=10,\end{array}\right.$ 解得$\left\{\begin{array}{l} x=\frac {26}{9},\\ t=\frac {10}{9},\end{array}\right.$
所以木棒切断处所表示的数为$\frac {26}{9}$。