《2025年一遍过八年级数学上册北师大版》

1 [2024武汉期末]解关于x,y的二元一次方程组 将①代入②,消去y后所得到的方程是(D)
A. $3x-4x-6= 8$
B. $3x+4x-6= 8$
C. $3x+4x+6= 8$
D. $3x-4x+6= 8$

答案： D 将①代入②，消去 y 后所得到的方程是 $3x - 2(2x - 3) = 8$，去括号，得 $3x - 4x + 6 = 8$。

二元一次方程组$\left\{\begin{array}{l} x+2y= 5,\\ y= 2x\end{array}\right. $的解是$\begin{cases}x = 1, \\ y = 2\end{cases}$。

答案： $\begin{cases}x = 1, \\ y = 2\end{cases}$ $\begin{cases}x + 2y = 5,① \\ y = 2x,②\end{cases}$ 把②代入①，得 $x + 4x = 5$，解得 $x = 1$，把 $x = 1$ 代入②，得 $y = 2$，所以方程组的解为 $\begin{cases}x = 1, \\ y = 2\end{cases}$。
解题通法
用代入消元法解二元一次方程组的一般步骤
(1) 从方程组中选定一个系数比较简单的方程进行变形，用含有 x(或 y) 的代数式表示 y(或 x)，即变成 $y = ax + b$（或 $x = ay + b$）的形式，其中 a，b 为常数且 $a \neq 0$；
(2) 将 $y = ax + b$（或 $x = ay + b$）代入另一个方程（不能代入原变形方程），消去 y(或 x)，得到一个关于 x(或 y) 的一元一次方程；
(3) 解这个一元一次方程，求出 x(或 y) 的值；
(4) 把 x(或 y) 的值代入 $y = ax + b$（或 $x = ay + b$），求出 y(或 x) 的值；
(5) 用“$\begin{cases}\end{cases}$”联立两个未知数的值，就是方程组的解。

3 用代入消元法解下列二元一次方程组：
(1)$\left\{\begin{array}{l} y= 2x+1,\\ 3x-2y= 2;\end{array}\right. $
解：$\begin{cases}y = 2x + 1,① \\ 3x - 2y = 2,②\end{cases}$
将①代入②，得 $3x - 2(2x + 1) = 2$，解得 $x=$-4，
将 $x=$-4代入①，得 $y=$-7，
所以原方程组的解为 $\begin{cases}x=$-4, \\ y=$-7\end{cases}$。
(2)$\left\{\begin{array}{l} y= \frac {2x-1}{3},\\ x+3y= 5。\end{array}\right. $
解：$\begin{cases}y = \frac{2x - 1}{3},① \\ x + 3y = 5,②\end{cases}$
将①代入②，得 $x + 2x - 1 = 5$，解得 $x=$2，
将 $x=$2代入①，得 $y=$1，
所以原方程组的解为 $\begin{cases}x=$2, \\ y=$1\end{cases}$。

答案： 解：
(1) $\begin{cases}y = 2x + 1,① \\ 3x - 2y = 2,②\end{cases}$
将①代入②，得 $3x - 2(2x + 1) = 2$，解得 $x = -4$，
将 $x = -4$ 代入①，得 $y = -7$，
所以原方程组的解为 $\begin{cases}x = -4, \\ y = -7\end{cases}$。
(2) $\begin{cases}y = \frac{2x - 1}{3},① \\ x + 3y = 5,②\end{cases}$
将①代入②，得 $x + 2x - 1 = 5$，解得 $x = 2$，
将 $x = 2$ 代入①，得 $y = 1$，
所以原方程组的解为 $\begin{cases}x = 2, \\ y = 1\end{cases}$。

4 用代入消元法解方程组 时,较简单的方法是(B)
A. 由①得$x= \frac {5+y}{2}$,再代入②
B. 由①得$y= 2x-5$,再代入②
C. 由②得$x= \frac {8+2y}{3}$,再代入①
D. 由②得$y= \frac {3x-8}{2}$,再代入①

答案： B

5 (1)完成框图中解方程组的过程：

(2)上面框图所示的解方程组的方法的名称是____。

答案：
解：
(1) 框图中解方程组的过程如下：

(2) 代入消元法

6 新趋势·过程性学习阅读下面的解题过程：
解方程组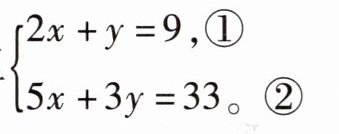
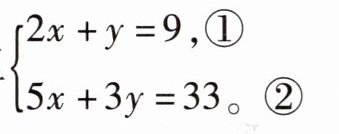
解:由①,得$y= 9-2x$,③
将③代入①,得$2x+9-2x= 9$,
所以$9= 9$,故此方程组无解。
以上解题过程是否正确？若不正确,请说明理由,并给出正确的解答过程。
不正确。理由：③是由①变形得到的，再将其代入①，肯定恒等，应将③代入②。
正确的解答过程：由①，得 $y = 9 - 2x$，③
把③代入②，得 $5x + 3(9 - 2x) = 33$，解得 $x = -6$。
把 $x = -6$ 代入③，得 $y = 21$。
所以原方程组的解为 $\begin{cases}x = -6, \\ y = 21\end{cases}$

答案： 解：不正确。理由：③是由①变形得到的，再将其代入①，肯定恒等，应将③代入②。
正确的解答过程：由①，得 $y = 9 - 2x$，③
把③代入②，得 $5x + 3(9 - 2x) = 33$，解得 $x = -6$。
把 $x = -6$ 代入③，得 $y = 21$。
所以原方程组的解为 $\begin{cases}x = -6, \\ y = 21\end{cases}$。

7 [2025兰州城关区期末]用代入消元法解下列二元一次方程组：
(1)$\left\{\begin{array}{l} 3x= 5y,\\ \frac {x}{4}+\frac {y}{3}= 3;\end{array}\right. $
解：原方程组可化为 $\begin{cases}3x = 5y,① \\ 3x + 4y = 36,②\end{cases}$
将①代入②，得 $5y + 4y = 36$，解得 $y=$4，
将 $y=$4代入①，得 $3x = 20$，解得 $x=$$\frac{20}{3}$，
故原方程组的解为 $\begin{cases}x=$$\frac{20}{3}$, \\ y=$4\end{cases}$。
(2)$\left\{\begin{array}{l} \frac {x}{3}-y+1= 0,\\ 2(x+1)-y= 6。\end{array}\right. $
解：$\begin{cases}\frac{x}{3} - y + 1 = 0,① \\ 2(x + 1) - y = 6,②\end{cases}$
由①，得 $x - 3y + 3 = 0$，即 $x=$$3y - 3$。③
由②，得 $2x - y = 4$，④
把③代入④，得 $2(3y - 3) - y = 4$，解得 $y=$2。
把 $y=$2代入③，得 $x=$3。
所以原方程组的解为 $\begin{cases}x=$3, \\ y=$2\end{cases}$。

答案： 解：
(1) 原方程组可化为 $\begin{cases}3x = 5y,① \\ 3x + 4y = 36,②\end{cases}$
将①代入②，得 $5y + 4y = 36$，解得 $y = 4$，
将 $y = 4$ 代入①，得 $3x = 20$，解得 $x = \frac{20}{3}$，
故原方程组的解为 $\begin{cases}x = \frac{20}{3}, \\ y = 4\end{cases}$。
(2) $\begin{cases}\frac{x}{3} - y + 1 = 0,① \\ 2(x + 1) - y = 6,②\end{cases}$
由①，得 $x - 3y + 3 = 0$，即 $x = 3y - 3$。③
由②，得 $2x - y = 4$，④
把③代入④，得 $2(3y - 3) - y = 4$，解得 $y = 2$。
把 $y = 2$ 代入③，得 $x = 3$。
所以原方程组的解为 $\begin{cases}x = 3, \\ y = 2\end{cases}$。