《2025年一遍过八年级数学上册北师大版》

13 [2024武威二十四中月考]下列运算错误的是(D)
A. $\sqrt {8}÷\sqrt {2}= 2$
B. $\sqrt {\frac {1}{2}}÷\sqrt {2}= \frac {1}{2}$
C. $\sqrt {3}÷\sqrt {\frac {3}{2}}= \sqrt {2}$
D. $\sqrt {\frac {2}{3}}÷\sqrt {\frac {3}{2}}= 1$

答案： D A 项，$\sqrt{8} \div \sqrt{2} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2$，不符合题意；B 项，$\sqrt{\frac{1}{2}} \div \sqrt{2} = \sqrt{\frac{1}{2} \times \frac{1}{2}} = \frac{1}{2}$，不符合题意；C 项，$\sqrt{3} \div \sqrt{\frac{3}{2}} = \sqrt{3 \times \frac{2}{3}} = \sqrt{2}$，不符合题意；D 项，$\sqrt{\frac{2}{3}} \div \sqrt{\frac{3}{2}} = \sqrt{\frac{2}{3} \times \frac{2}{3}} = \frac{2}{3} \neq 1$，符合题意。

14 [2024云浮期中]计算$\sqrt {20}×\frac {\sqrt {3}}{4}÷\sqrt {15}$的结果是(A)
A. $\frac {1}{2}$
B. 1
C. $\frac {\sqrt {5}}{2}$
D. $\frac {5}{2}$

答案： A $\sqrt{20} \times \frac{\sqrt{3}}{4} \div \sqrt{15} = \frac{\sqrt{20 \times 3 \div 15}}{4} = \frac{\sqrt{4}}{4} = \frac{2}{4} = \frac{1}{2}$。

15 [2024阳江江城区期中]若$\sqrt {2}×\sqrt {\frac {6}{x}}$是整数,则整数x的值是(3或12)
A. 1或3
B. 3或6
C. 3或12
D. 6或12

答案： C $\sqrt{2} \times \sqrt{\frac{6}{x}} = \sqrt{\frac{12}{x}}$，则当整数$x$为 3 或 12 时，$\sqrt{2} \times \sqrt{\frac{6}{x}}$为整数。

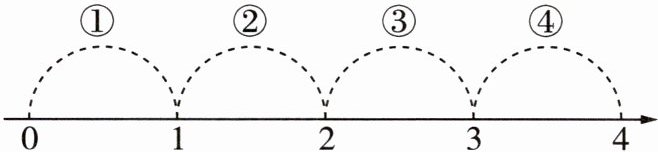
如图,若计算$\sqrt {\frac {1}{2}}×\sqrt {24}$的结果为a,则数a对应的点落在了数轴上的④段。

答案： ④ $\sqrt{\frac{1}{2}} \times \sqrt{24} = \sqrt{\frac{1}{2} \times 24} = \sqrt{12}$，因为$9 ＜ 12 ＜ 16$，所以$3 ＜ \sqrt{12} ＜ 4$，所以数$a$对应的点落在了数轴上的④段。

17 [2025百色期中]计算:$\sqrt {1\frac {2}{3}}÷\sqrt {2\frac {1}{3}}×\sqrt {1\frac {2}{5}}=$1。

答案： 1 $\sqrt{1\frac{2}{3}} \div \sqrt{2\frac{1}{3}} \times \sqrt{1\frac{2}{5}} = \sqrt{\frac{5}{3} \div \frac{7}{3} \times \frac{7}{5}} = 1$。

18 计算:
(1)[2025沈阳沈河区期末]$(\sqrt {\frac {9}{2}}-\frac {\sqrt {98}}{3})÷\sqrt {2}+\frac {1}{3}$;
(2)[2025郑州期末]$\frac {\sqrt {20}+\sqrt {5}}{\sqrt {5}}-(\sqrt {3}+\sqrt {2})×(\sqrt {3}-\sqrt {2})$。

答案： 解：
(1)$(\sqrt{\frac{9}{2}} - \frac{\sqrt{98}}{3}) \div \sqrt{2} + \frac{1}{3}$
$= \frac{3}{2} - \frac{7}{3} + \frac{1}{3}$
$= \frac{3}{2} - 2$
$= -\frac{1}{2}$。
(2)$\frac{\sqrt{20} + \sqrt{5}}{\sqrt{5}} - (\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2})$
$= 2 + 1 - (3 - 2)$
$= 3 - 1$
$= 2$。

19 新趋势·过程性学习 [2025长春期末节选]阅读材料,回答下列问题。
【材料一】两个含有二次根式且非零的代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式。例如:$\sqrt {2}×\sqrt {2}= 2,(\sqrt {3}+1)×(\sqrt {3}-1)= 2$,我们称$\sqrt {2}和\sqrt {2}$互为有理化因式,$\sqrt {3}+1和\sqrt {3}-1$互为有理化因式。
(1)$\sqrt {5}$的有理化因式是____$\sqrt{5}$____,$2-\sqrt {3}$的有理化因式是____$2 + \sqrt{3}$____;(写出一个即可)
【材料二】将代数式分子、分母同乘分子的有理化因式,从而消去分子中的根式,这种变形叫作分子有理化。例如:$\sqrt {3}-\sqrt {2}=\frac {(\sqrt {3}-\sqrt {2})(\sqrt {3}+\sqrt {2})}{\sqrt {3}+\sqrt {2}}= \frac {1}{\sqrt {3}+\sqrt {2}}$。
(2)用分子有理化直接比较$\sqrt {n+1}-\sqrt {n}和\sqrt {n}-\sqrt {n-1}(n≥2)$的大小。
解：$\sqrt{n + 1} - \sqrt{n} = \frac{(\sqrt{n + 1} - \sqrt{n})(\sqrt{n + 1} + \sqrt{n})}{\sqrt{n + 1} + \sqrt{n}} = \frac{n + 1 - n}{\sqrt{n + 1} + \sqrt{n}} = \frac{1}{\sqrt{n + 1} + \sqrt{n}}$，
$\sqrt{n} - \sqrt{n - 1} = \frac{(\sqrt{n} - \sqrt{n - 1})(\sqrt{n} + \sqrt{n - 1})}{\sqrt{n} + \sqrt{n - 1}} = \frac{n - (n - 1)}{\sqrt{n} + \sqrt{n - 1}} = \frac{1}{\sqrt{n} + \sqrt{n - 1}}$，
因为$\sqrt{n + 1} ＞ \sqrt{n - 1}$，所以$\frac{1}{\sqrt{n + 1} + \sqrt{n}} ＜ \frac{1}{\sqrt{n} + \sqrt{n - 1}}$，
所以$\sqrt{n + 1} - \sqrt{n} ＜ \sqrt{n} - \sqrt{n - 1}$。

答案： 解：
(1)（答案不唯一）$\sqrt{5}$ $2 + \sqrt{3}$
(2)$\sqrt{n + 1} - \sqrt{n} = \frac{(\sqrt{n + 1} - \sqrt{n})(\sqrt{n + 1} + \sqrt{n})}{\sqrt{n + 1} + \sqrt{n}} = \frac{n + 1 - n}{\sqrt{n + 1} + \sqrt{n}} = \frac{1}{\sqrt{n + 1} + \sqrt{n}}$，
$\sqrt{n} - \sqrt{n - 1} = \frac{(\sqrt{n} - \sqrt{n - 1})(\sqrt{n} + \sqrt{n - 1})}{\sqrt{n} + \sqrt{n - 1}} = \frac{n - (n - 1)}{\sqrt{n} + \sqrt{n - 1}} = \frac{1}{\sqrt{n} + \sqrt{n - 1}}$，
因为$\sqrt{n + 1} ＞ \sqrt{n - 1}$，所以$\frac{1}{\sqrt{n + 1} + \sqrt{n}} ＜ \frac{1}{\sqrt{n} + \sqrt{n - 1}}$，
所以$\sqrt{n + 1} - \sqrt{n} ＜ \sqrt{n} - \sqrt{n - 1}$。