《2025年一遍过八年级数学上册北师大版》

1 若一条直线经过点$A(-1,1)和B(1,5)$,则这条直线的函数表达式为$ y = 2x + 3 $。

答案： $ y = 2x + 3 $ 设这条直线的函数表达式为 $ y = kx + b $，因为这条直线经过点 $ A(-1,1) $ 和 $ B(1,5) $，所以 $ \begin{cases} -k + b = 1, \\ k + b = 5, \end{cases} $ 解得 $ \begin{cases} k = 2, \\ b = 3, \end{cases} $ 所以这条直线的函数表达式为 $ y = 2x + 3 $。
解题通法
用二元一次方程组确定一次函数表达式的一般步骤
(1) 设一次函数的表达式为 $ y = kx + b(k \neq 0) $；
(2) 将满足一次函数的两组数值分别代入 $ y = kx + b(k \neq 0) $ 中，得到关于 $ k $，$ b $ 的二元一次方程组；
(3) 解二元一次方程组，求出 $ k $，$ b $ 的值；
(4) 将 $ k $，$ b $ 的值代入 $ y = kx + b $，即可确定一次函数的表达式。

已知$y是x$的一次函数,下表列出了部分对应值：

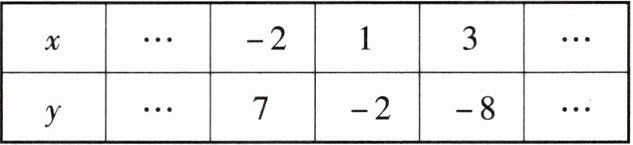
则$y与x$的函数表达式为$ y = -3x + 1 $。

答案： $ y = -3x + 1 $ 设 $ y $ 与 $ x $ 的函数表达式为 $ y = kx + b(k \neq 0) $，将 $ (-2,7) $，$ (1,-2) $ 代入 $ y = kx + b $，得 $ \begin{cases} -2k + b = 7, \\ k + b = -2, \end{cases} $ 解得 $ \begin{cases} k = -3, \\ b = 1, \end{cases} $ 所以 $ y $ 与 $ x $ 的函数表达式为 $ y = -3x + 1 $。

3 [2024西宁海湖中学开学考试]如图,一次函数$y= kx+b(k\neq 0)的图象经过A(1,3)$,$B(-2,-1)$两点。
(1)求此一次函数的表达式；
(2)若该一次函数与$x轴交于C$点,求$\triangle AOC$的面积。
(1)此一次函数的表达式为$y=$$\frac{4}{3}x + \frac{5}{3}$。
(2)$\triangle AOC$的面积为$\frac{15}{8}$。

答案： 解：
(1) 把 $ A(1,3) $，$ B(-2,-1) $ 的坐标代入 $ y = kx + b $，得 $ \begin{cases} k + b = 3, \\ -2k + b = -1, \end{cases} $ 解得 $ \begin{cases} k = \frac{4}{3}, \\ b = \frac{5}{3}, \end{cases} $ 所以一次函数的表达式为 $ y = \frac{4}{3}x + \frac{5}{3} $。
(2) 把 $ y = 0 $ 代入 $ y = \frac{4}{3}x + \frac{5}{3} $，得 $ \frac{4}{3}x + \frac{5}{3} = 0 $，解得 $ x = -\frac{5}{4} $，所以直线 $ AB $ 与 $ x $ 轴的交点 $ C $ 为 $ (-\frac{5}{4},0) $，所以 $ \triangle AOC $ 的面积为 $ \frac{1}{2} \times \frac{5}{4} \times 3 = \frac{15}{8} $。

4 跨学科·生物[2024陕西中考副卷]实验表明,在某地,温度在$15^{\circ}C至25^{\circ}C$的范围内,一种蟋蟀$1\min的平均鸣叫次数y可近似看成该地当时温度x(^{\circ}C)$的一次函数。已知这种蟋蟀在温度为$16^{\circ}C$时,$1\min平均鸣叫92$次；在温度为$23^{\circ}C$时,$1\min平均鸣叫155$次。
(1)求$y与x$之间的函数表达式。
(2)当这种蟋蟀$1\min平均鸣叫128$次时,该地当时的温度约是多少？

答案： 解：
(1) 设 $ y $ 与 $ x $ 之间的函数表达式为 $ y = kx + b(k \neq 0) $，将 $ x = 16 $，$ y = 92 $ 和 $ x = 23 $，$ y = 155 $ 分别代入 $ y = kx + b $，得 $ \begin{cases} 16k + b = 92, \\ 23k + b = 155, \end{cases} $ 解得 $ \begin{cases} k = 9, \\ b = -52, \end{cases} $ 所以 $ y $ 与 $ x $ 之间的函数表达式为 $ y = 9x - 52(15 \leq x \leq 25) $。
(2) 将 $ y = 128 $ 代入 $ y = 9x - 52 $，得 $ 9x - 52 = 128 $，解得 $ x = 20 $，所以该地当时的温度约是 $ 20^{\circ}C $。

5 新情境[2024长春中考]区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度。小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶$\frac{1}{12}$小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时。汽车在区间测速路段行驶的路程$y$(千米)与在此路段行驶的时间$x$(时)之间的函数图象如图所示。

(1)$a$的值为______$\frac{1}{5}$；
(2)当$\frac{1}{12}\leq x\leq a$时,求$y与x$之间的函数关系式；
$y=90x+2\left(\frac{1}{12}\leq x\leq \frac{1}{5}\right)$
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速。(此路段要求小型汽车行驶速度不得超过120千米/时)
这辆汽车减速前没有超速。

答案： 解：
(1) $ \frac{1}{5} $ 由题意，得 $ 100a = 20 $，解得 $ a = \frac{1}{5} $。
(2) 设当 $ \frac{1}{12} \leq x \leq \frac{1}{5} $ 时，$ y $ 与 $ x $ 之间的函数关系式为 $ y = kx + b(k \neq 0) $，则 $ \begin{cases} \frac{1}{6}k + b = 17, \\ \frac{1}{5}k + b = 20, \end{cases} $ 解得 $ \begin{cases} k = 90, \\ b = 2, \end{cases} $ 所以 $ y = 90x + 2(\frac{1}{12} \leq x \leq \frac{1}{5}) $。
(3) 当 $ x = \frac{1}{12} $ 时，$ y = 90 \times \frac{1}{12} + 2 = \frac{19}{2} $，所以匀速行驶 $ \frac{1}{12} $ 小时期间的速度为 $ \frac{19}{2} \div \frac{1}{12} = 114 $（千米/时），因为 $ 114 ＜ 120 $，所以这辆汽车减速前没有超速。
归纳总结
(1) 在实际问题中，可根据图象、素材、表格等信息提取相关的量作为自变量和函数值来确定一次函数的表达式。
(2) 在解决实际问题时，要用函数的观点看待问题，并将其转化为二元一次方程组来解决，体会方程思想和转化思想在实际问题中的应用。