《2025年一遍过八年级数学上册北师大版》

7 [2025沈阳期末]杜甫曾经哀叹“茅屋为秋风所破”。现在我们来看一茅屋的屋顶剖面(如图),它呈等腰三角形,如果屋檐AB= AC= 5米,横梁BC= 8米,那么从梁BC上的任意一点D要支一根木头顶住屋顶A处,这根木头需要长度可能是 (C)
A.2.5米
B.6米
C.4米
D.8米

答案： 1. 首先求等腰三角形$ABC$底边$BC$上的高$h$：
设$BC$中点为$E$，因为$AB = AC = 5$米，$BC = 8$米，根据等腰三角形三线合一性质，$AE\perp BC$，$BE=\frac{1}{2}BC = 4$米。
在$Rt\triangle ABE$中，根据勾股定理$a^{2}+b^{2}=c^{2}$（这里$c = AB$，$a = BE$，$b = AE$），则$AE=\sqrt{AB^{2}-BE^{2}}$。
把$AB = 5$，$BE = 4$代入可得：$AE=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=\sqrt{9}=3$米。
2. 然后根据垂线段最短：
从$A$到$BC$的垂线段$AE$最短，$AE = 3$米；$AB = AC = 5$米是$A$到$BC$上点的最长距离（当$D$与$B$或$C$重合时）。
所以$3\leqslant AD\leqslant5$。
所以这根木头长度可能是$4$米，答案是C。

8 教材习题变式[2024吕梁期末]现有一楼房发生火灾,消防队员用消防车上的云梯救人。如图,已知消防车高3m,云梯最多只能伸长到15m。救人时云梯伸长至最长,在完成从12m高处救人后,还要从15m高处救人。这时消防车要从原处向着火的楼房靠近的距离MN为 (3m)

A.3m
B.5m
C.7m
D.9m

答案： 8 A 在$Rt△ABO$中，$∠AOB = 90^{\circ}$，$AB = 15m$，$OB = 12 - 3 = 9(m)$，所以$AO^{2} = AB^{2} - OB^{2} = 15^{2} - 9^{2} = 144$，所以$AO = 12m$。在$Rt△COD$中，$∠COD = 90^{\circ}$，$CD = 15m$，$OD = 15 - 3 = 12(m)$，所以$OC^{2} = CD^{2} - OD^{2} = 15^{2} - 12^{2} = 81$，所以$OC = 9m$，所以$AC = AO - OC = 12 - 9 = 3(m)$，所以消防车要从原处向着火的楼房靠近的距离$MN = AC = 3m$。

9 教材复习题变式[2025成都期末]国庆假期中,小华与同学去玩探宝游戏,按照探宝图,如图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是______km。

答案：
10 如图，过点$B$作$BC⊥AC$，垂足为$C$，延长$ND$交$AC$于点$M$。由图形可知$AC = AF - MF + MC = 8 - 3 + 1 = 6(km)$，$BC = 2 + 6 = 8(km)$，在$Rt△ACB$中，由勾股定理，得$AB = 10km$，即门口$A$到藏宝点$B$的直线距离是$10km$。

10 [2024郑州期中]如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移到离该灯5m及5m内的位置,灯就会自动发光。若小明身高1.5m,则他走到离墙______m的地方灯刚好自动发光。

答案：
4 如图，设小明走到点$C$的位置时，头顶$D$与传感器$A$的距离是$5m$，灯刚好自动发光，过点$D$作$DE⊥AB$于点$E$，则$AE = 4.5 - 1.5 = 3(m)$。在$Rt△ADE$中，$DE^{2} = AD^{2} - AE^{2} = 5^{2} - 3^{2} = 16$，所以$DE = 4m$，所以小明走到离墙$4m$的地方灯刚好自动发光。

11 [2024济宁任城区期末]某品牌婴儿车的简化结构示意图如图所示。根据安全标准,需满足BC⊥CD,现测得AB= CD= 6dm,BC= 3dm,AD= 9dm,其中AB与BD之间是由一个角固定为90°的零件连接的(即∠ABD= 90°),该车是否符合安全标准?请通过计算说明。

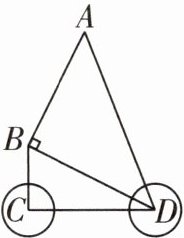
解：在$Rt△ABD$中，$BD^{2} = AD^{2} - AB^{2} = 9^{2} - 6^{2} = 45$，
在$△BCD$中，$BC^{2} + CD^{2} = 3^{2} + 6^{2} = 45$，
所以$BC^{2} + CD^{2} = BD^{2}$，
所以$∠BCD = 90^{\circ}$，所以$BC⊥CD$。
故该车符合安全标准。符合安全标准

答案： 解：在$Rt△ABD$中，$BD^{2} = AD^{2} - AB^{2} = 9^{2} - 6^{2} = 45$，
在$△BCD$中，$BC^{2} + CD^{2} = 3^{2} + 6^{2} = 45$，
所以$BC^{2} + CD^{2} = BD^{2}$，
所以$∠BCD = 90^{\circ}$，所以$BC⊥CD$。
故该车符合安全标准。

12 教材习题变式[2025无锡新吴区月考]一辆装满货物的卡车,其外形高2.5m,宽1.6m,某工厂的厂门形状及尺寸如图所示(上部是半圆形,下部是长方形)。这辆卡车能否通过该工厂的厂门?并说明理由。

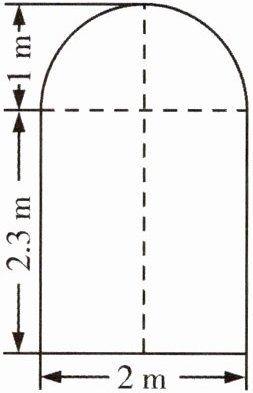
解：卡车能通过该工厂的厂门。理由如下：
如图，点$D$距厂门的中心线0.8m，过点$D$作$CH⊥AB$，与地面交于点$H$，与厂门上方圆弧交于点$C$，连接$OC$。
易知$OC = $1m，$OD = 0.8m$。
在$Rt△OCD$中，由勾股定理，
得$CD^{2} = OC^{2} - OD^{2} = 1^{2} - 0.8^{2} = $0.36，
所以$CD = $0.6m，所以$CH = 0.6 + $2.3$ = 2.9(m)$，
因为$2.9 ＞ 2.5$，所以这辆卡车能通过该工厂的厂门。

答案： 解：卡车能通过该工厂的厂门。理由如下：
如图，点$D$距厂门的中心线$0.8m$，过点$D$作$CH⊥AB$，与地面交于点$H$，与厂门上方圆弧交于点$C$，连接$OC$。
易知$OC = 1m$，$OD = 0.8m$。
在$Rt△OCD$中，由勾股定理，
得$CD^{2} = OC^{2} - OD^{2} = 1^{2} - 0.8^{2} = 0.36$，
所以$CD = 0.6m$，所以$CH = 0.6 + 2.3 = 2.9(m)$，
因为$2.9 ＞ 2.5$，所以这辆卡车能通过该工厂的厂门。
名师点睛
本题考查了勾股定理在实际生活中的应用，解题的关键是借助相关的数据构建直角三角形，进而运用勾股定理求解。

13 推理能力[2024兰州树人中学期末]如图是高空秋千的示意图,小红从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处。若∠AOC= 90°,点A与点B的高度差AD= 1米,水平距离BD= 4米,则点C与点B的高度差CE为______米。

答案：
4.5 如图，过点$A$作$AF⊥BO$于点$F$，过点$C$作$CG⊥BO$于点$G$。因为$∠AOC = ∠AOF + ∠COG = 90^{\circ}$，$∠AOF + ∠OAF = 90^{\circ}$，所以$∠COG = ∠OAF$。在$△AOF$和$△OCG$中，$\left\{\begin{array}{l} ∠AFO = ∠OGC,\\ ∠OAF = ∠COG,\\ AO = OC,\end{array}\right.$所以$△AOF≌△OCG$，所以$OG = AF = BD = 4$米。设$AO = x$米，在$Rt△AFO$中，$AF^{2} + OF^{2} = AO^{2}$，即$4^{2} + (x - 1)^{2} = x^{2}$，解得$x = 8.5$。则$OB = AO = 8.5$米，$CE = GB = OB - OG = 8.5 - 4 = 4.5$（米）。