《2025年一遍过八年级数学上册北师大版》

9 [2025滁州二模]已知正整数m,n满足：$m＜\sqrt [3]{10}\lt m+1$,$n＜\sqrt {12}\lt n+1$。则$m^{n}$的值为(8)
A. 4
B. 8
C. 9
D. 27

答案： B 因为$\sqrt[3]{8}＜\sqrt[3]{10}＜\sqrt[3]{27}$，$\sqrt{9}＜\sqrt{12}＜\sqrt{16}$，所以$2＜\sqrt[3]{10}＜3$，$3＜\sqrt{12}＜4$，又因为$m＜\sqrt[3]{10}＜m+1$，$n＜\sqrt{12}＜n+1$，所以$m=2$，$n=3$，所以$m^{n}=2^{3}=8$。

10 教材习题变式[2024保定期中]某计算器中有$\sqrt {}$,$1/x$,$x^{2}$三个按键,以下是这三个按键的功能。

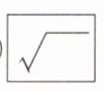
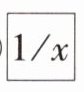
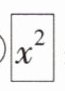
①$\sqrt {}$：将荧幕显示的数变成它的算术平方根。
②$1/x$：将荧幕显示的数变成它的倒数。
③$x^{2}$：将荧幕显示的数变成它的平方。
如图,小明输入一个数据后,依次按照从第1步到第3步循环按键。

第1步 第2步 第3步
若一开始输入的数据为5,那么第2024步之后,显示的结果是(0.04)
A. 5
B. 0.2
C. 0.04
D. 25

答案： C 由题意知，第1步结果为$5^{2}=25$，第2步结果为$\frac{1}{25}=0.04$，第3步结果为$\sqrt{0.04}=0.2$，第4步结果为$0.2^{2}=0.04$，第5步结果为$\frac{1}{0.04}=25$，第6步结果为$\sqrt{25}=5$，第7步结果为$5^{2}=25\cdots\cdots$所以运算的结果以25，0.04，0.2，0.04，25，5这六个数循环出现，因为$2024÷6=337\cdots\cdots2$，所以第2024步之后显示的结果为0.04。

11 新趋势·数学文化[2024安徽中考]我国古代数学家张衡将圆周率取值为$\sqrt {10}$,祖冲之给出圆周率的一种分数形式的近似值为$\frac {22}{7}$。比较大小：$\sqrt {10}$＞$\frac {22}{7}$。(填“＞”或“＜”)

答案： $＞$ $(\sqrt{10})^{2}=10$，$(\frac{22}{7})^{2}=\frac{484}{49}$，因为$10＞\frac{484}{49}$，所以$\sqrt{10}＞\frac{22}{7}$。

12 教材习题变式利用计算器,比较下列各组数的大小：(1)$\sqrt {18}$＞$\sqrt [3]{35}$；(2)$\frac {8}{13}$＜$\frac {\sqrt {6}-1}{2}$。(填“＞”“＜”或“=”)

答案：
(1)$＞$；
(2)$＜$

13 [2024河北中考]已知a,b,n均为正整数。
(1)若$n＜\sqrt {10}\lt n+1$,则n=3
(2)若$n-1＜\sqrt {a}\lt n$,$n＜\sqrt {b}\lt n+1$,则满足条件的a的个数总比b的个数少2个。

答案： 解:
(1)3
因为$\sqrt{9}＜\sqrt{10}＜\sqrt{16}$，所以$3＜\sqrt{10}＜4$，因为$n＜\sqrt{10}＜n+1$，$n$为正整数，所以$n=3$。
(2)2
因为$n-1＜\sqrt{a}＜n$，所以$(n-1)^{2}＜a＜n^{2}$，所以$a$的个数为$n^{2}-(n-1)^{2}-1=n^{2}-n^{2}+2n-1-1=2n-2$，因为$n＜\sqrt{b}＜n+1$，所以$n^{2}＜b＜(n+1)^{2}$，所以$b$的个数为$(n+1)^{2}-n^{2}-1=n^{2}+2n+1-n^{2}-1=2n$，因为$2n-(2n-2)=2$，所以满足条件的$a$的个数总比$b$的个数少2个。

14 (1)利用计算器,将下列各数用“＜”排列起来：
$\sqrt {1}+\sqrt {12}$,$\sqrt {2}+\sqrt {11}$,$\sqrt {3}+\sqrt {10}$,$\sqrt {4}+\sqrt {9}$,$\sqrt {5}+\sqrt {8}$,$\sqrt {6}+\sqrt {7}$。
(2)上面各数有什么共同的特征？由此能得出什么结论？

答案： 解:
(1)$\sqrt{1}+\sqrt{12}＜\sqrt{2}+\sqrt{11}＜\sqrt{3}+\sqrt{10}＜\sqrt{4}+\sqrt{9}＜\sqrt{5}+\sqrt{8}＜\sqrt{6}+\sqrt{7}$。
(2)共同特征:它们都是两个数的算术平方根的和的形式，而且两根号内数的和都是13。
结论:当根号内两数越来越接近时，和越来越大。

15 新趋势·过程性学习[2024沈阳于洪区期末]小李同学探索$\sqrt {86}$的近似值的过程如下：
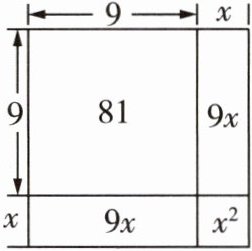
因为面积为86的正方形的边长是$\sqrt {86}$,且$9＜\sqrt {86}＜10$,
所以设$\sqrt {86}= 9+x$,其中$0\lt x＜1$,画出示意图,如图所示。
根据示意图,可得图中正方形的面积$S_{正方形}= 81+2×9x+x^{2}$,
又因为$S_{正方形}= 86$,所以$81+2×9x+x^{2}= 86$。
当$x^{2}＜1$时,可忽略$x^{2}$,得$81+18x≈86$,解得$x≈0.28$,所以$\sqrt {86}≈9.28$。
(1)填空：$\sqrt {157}$的整数部分的值为____；
(2)仿照上述方法,探究$\sqrt {157}$的近似值。(结果精确到0.01)
(答题要求：画出示意图,标明数据,并写出求解过程)

答案：
解:
(1)12
因为$144＜157＜169$，所以$\sqrt{144}＜\sqrt{157}＜\sqrt{169}$，即$12＜\sqrt{157}＜13$，所以$\sqrt{157}$的整数部分的值为12。
(2)如图，图中正方形的面积$S_{正方形}=144+2\times12x+x^{2}$，
又因为$S_{正方形}=157$，所以$144+2\times12x+x^{2}=157$。
当$x^{2}＜1$时，可忽略$x^{2}$，得$144+24x\approx157$，
解得$x\approx0.54$，
所以$\sqrt{157}\approx12.54$。