《2025年一遍过八年级数学上册北师大版》

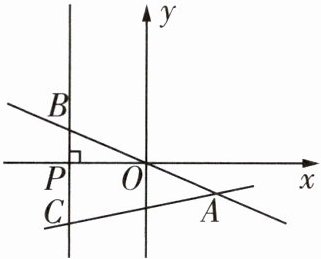
1 [2025西安爱知中学期中]如图,在平面直角坐标系中,已知正比例函数$y= -\frac {5}{12}x与一次函数y= \frac {1}{4}x-8$的图象交于点A。设x轴上一点$P(a,0)$,过点P作x轴的垂线(垂线位于y轴的左侧),分别交$y= -\frac {5}{12}x和y= \frac {1}{4}x-8$的图象于点B,C,若$BC= \frac {16}{13}OA$,则a的值为(-12)

A. -13
B. -12
C. -11
D. -10

答案： B 由题意，得$\left\{\begin{array}{l} y=-\frac {5}{12}x\\ y=\frac {1}{4}x-8\end{array}\right. $，解得$\left\{\begin{array}{l} x=12\\ y=-5\end{array}\right. $，所以$A(12,-5)$，所以$OA=\sqrt{(12 - 0)^{2}+(-5 - 0)^{2}}=\sqrt{12^{2}+5^{2}} = 13$，所以$BC=\frac{16}{13}OA=\frac{16}{13}×13 = 16$。因为$P(a,0)$，所以$B(a,-\frac{5}{12}a)$，$C(a,\frac{1}{4}a - 8)$，所以$BC=-\frac{5}{12}a-(\frac{1}{4}a - 8)=-\frac{5}{12}a-\frac{1}{4}a + 8=-\frac{2}{3}a + 8$，所以$-\frac{2}{3}a + 8 = 16$，解得$a = -12$。

2 已知$A(-1,5),B(-2,4)$,C在x轴上,D在y轴上,当四边形ABCD的周长最小时,直线CD的表达式为______。

答案：
$y = 3x + 2$ 如图，作$A$关于$y$轴的对称点$A'$，作$B$关于$x$轴的对称点$B'$，连接$A'B'$，交$x$轴于$C$，交$y$轴于$D$，易知$A'B'$的长就是$AD + CD + BC$的最小值，因为$AB$的长为定值，所以此时四边形$ABCD$的周长最小。设直线$CD$的表达式为$y = kx + b$，因为点$A(-1,5)$关于$y$轴的对称点$A'$的坐标是$(1,5)$，点$B(-2,4)$关于$x$轴的对称点$B'$的坐标是$(-2,-4)$，所以$\left\{\begin{array}{l} k + b = 5\\ -2k + b = -4\end{array}\right. $，解得$\left\{\begin{array}{l} k = 3\\ b = 2\end{array}\right. $，所以直线$CD$的表达式为$y = 3x + 2$。

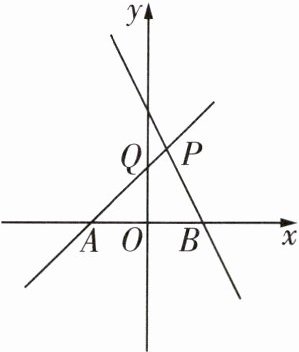
3 [2025萍乡期末]如图,一次函数$y= x+1$的图象分别与x轴,y轴交于点A,Q,一次函数$y= -2x+2$的图象与x轴交于点B,与$y= x+1$的图象交于点P。
(1)求A,B,P三点的坐标;A(-1,0),B(1,0),P($\frac{1}{3}$,$\frac{4}{3}$);
(2)求四边形PQOB的面积。四边形PQOB的面积为$\frac{5}{6}$。

程组与一次函数的综合

答案： 解：
(1)因为一次函数$y = x + 1$的图象与$x$轴交于点$A$，所以$A(-1,0)$，因为一次函数$y = -2x + 2$的图象与$x$轴交于点$B$，所以$B(1,0)$，由$\left\{\begin{array}{l} y = x + 1\\ y = -2x + 2\end{array}\right. $，解得$\left\{\begin{array}{l} x = \frac{1}{3}\\ y = \frac{4}{3}\end{array}\right. $，所以$P(\frac{1}{3},\frac{4}{3})$。
(2)由一次函数$y = x + 1$的图象与$y$轴交于点$Q$，得$Q(0,1)$，所以四边形$PQOB$的面积为$S_{\triangle APB}-S_{\triangle AQO}=\frac{1}{2}×\frac{4}{3}×2-\frac{1}{2}×1×1=\frac{5}{6}$。

4 [2024青岛市北区期末]爆竹声中一岁除,春风送暖入屠苏。春节前期,家家户户贴春联,挂灯笼,欢天喜地迎新年。某百货超市计划购进春联和灯笼这两种商品。已知第一次购进5个灯笼和4副春联花费185元,第二次购进3个灯笼和8副春联花费195元。
(1)求每个灯笼和每副春联的进价分别是多少元。
(2)由于灯笼和春联畅销,超市决定第三次购进灯笼和春联这两种商品共300件,其中灯笼的数量不低于75个,且灯笼和春联的进价保持不变。若每个灯笼的售价为30元,每副春联的售价为25元,在销售中灯笼有4%的损坏,春联有8%的损坏。若第三次购进的灯笼和春联全部售出(损坏的灯笼和春联不能售出),请问当第三次购进多少个灯笼时,可使本次销售获得最大利润,最大利润是多少元。

答案： 解：
(1)设每个灯笼和每副春联的进价分别是$x$元和$y$元，根据题意，得$\left\{\begin{array}{l} 5x + 4y = 185\\ 3x + 8y = 195\end{array}\right. $，解得$\left\{\begin{array}{l} x = 25\\ y = 15\end{array}\right. $，所以每个灯笼和每副春联的进价分别是$25$元和$15$元。
(2)设第三次购进灯笼$m$个，那么购进春联$(300 - m)$副，$75\leq m\leq300$。设第三次购进的灯笼和春联全部售出(损坏的灯笼和春联不能售出)获得的利润为$w$元，根据题意，得$w = 30×(1 - 4\%)m + 25×(1 - 8\%)(300 - m)-25m - 15(300 - m)=-4.2m + 2400$，因为$-4.2\lt0$，所以$w$随$m$的增大而减小，因为$75\leq m\leq300$，所以当$m = 75$时，$w$最大，此时$w=-4.2×75 + 2400 = 2085$，所以当第三次购进$75$个灯笼时，可使本次销售获得最大利润，最大利润是$2085$元。