《2025年一遍过八年级数学上册北师大版》

14 [2024廊坊广阳区期中]下列说法中不正确的个数是(D)
①$(-5)^{2}的平方根是\pm 5$；②$-a^{2}$没有平方根；③非负数a的平方根是非负数；④因为负数没有平方根,所以平方根不可能为负；⑤0和1的平方根等于本身。
A. 1
B. 2
C. 3
D. 4

答案： D $a=0$时，$-a^{2}$有平方根，故②错误；正数有两个平方根，它们互为相反数，故③错误；负数没有平方根，一个正数的平方根有两个，互为相反数，故④错误；0的平方根等于它本身，1的平方根是$\pm 1$，故⑤错误。

15 [2024沧州期末]如果一个自然数的平方根是$\pm a(a\geq 0)$,那么与这个自然数相邻的下一个自然数的平方根为(C)
A. $\pm (a+1)$
B. $\pm a+1$
C. $\pm \sqrt{a^{2}+1}$
D. $\pm \sqrt{a+1}$

答案： C 因为一个自然数的平方根是$\pm a$，所以这个自然数是$a^{2}$，所以相邻的下一个自然数是$a^{2}+1$，所以$a^{2}+1$的平方根是$\pm \sqrt{a^{2}+1}$。

16 [2024保定竞秀区期中]如果$a+3$和$2a-15$是某个正数的两个平方根,那么这个正数是(49)
A. 49
B. 441
C. 21
D. 7

答案： A 由题意知$a+3=-(2a-15)$，解得$a=4$，所以$a+3=7$，所以$7^{2}=49$。故这个正数是49。

17 [2024金华五校期中]已知$3a^{m}b^{8}与-\frac{1}{10}b^{n}a^{3}$的和是单项式,则$n^{2}-m^{2}$的平方根是$\pm \sqrt{55}$。

答案： $\pm \sqrt{55}$ 因为$3a^{m}b^{8}$与$-\frac{1}{10}b^{n}a^{3}$的和是单项式，所以$m=3$，$n=8$，所以$\pm \sqrt{n^{2}-m^{2}}=\pm \sqrt{55}$。

若$x+1$是16的一个平方根,则x的值为3或-5。

答案： 3或-5 因为$(\pm 4)^{2}=16$，所以16的平方根是$\pm 4$。当$x+1=4$时，$x=3$；当$x+1=-4$时，$x=-5$。(注意：一个正数有两个平方根)

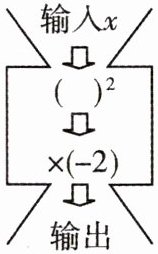
19 如图是一数值转换机,若输出的结果为-32,则输入的x值为±4。

答案： $\pm 4$ 由题意，得$x^{2}×(-2)=-32$，所以$x^{2}=16$。因为$(\pm 4)^{2}=16$，所以$x=\pm 4$。

20 求下列各式中x的值：
(1)$(3x-1)^{2}-64= 0$；$x=3$或$x=-\frac{7}{3}$
(2)$2(x-1)^{2}-18= 0$。$x=4$或$x=-2$

答案： 解：
(1)由$(3x-1)^{2}-64=0$可得，$(3x-1)^{2}=64$。
因为$(\pm 8)^{2}=64$，所以$3x-1=8$或$3x-1=-8$，
所以$x=3$或$x=-\frac{7}{3}$。
(2)由$2(x-1)^{2}-18=0$可得，$(x-1)^{2}=9$。
因为$(\pm 3)^{2}=9$，所以$x-1=3$或$x-1=-3$，
所以$x=4$或$x=-2$。

21 [2024泉州六中月考]已知正数x的平方根是m和$m+b(b\neq 0)$。
(1)若$b= 8$,求m的值；-4
(2)若$m^{2}x+(m+b)^{2}x= 4$,求x的值。$\sqrt{2}$

答案： 解：
(1)因为正数x的平方根是m和$m+b(b≠0)$，
所以$m+m+b=0$，
又因为$b=8$，所以$2m+8=0$，
所以$m=-4$。
(2)因为正数x的平方根是m和$m+b(b≠0)$，
所以$(m+b)^{2}=x$，$m^{2}=x$。
因为$m^{2}x+(m+b)^{2}x=4$，
所以$x^{2}+x^{2}=4$，所以$x^{2}=2$，
又因为$x＞0$，所以$x=\sqrt{2}$。

22 新趋势·过程性学习[2024芜湖月考]甲、乙两人计算$a+\sqrt{1-2a+a^{2}}$的值,当$a= 3$时,得到下面不同的答案。
甲的解答：$a+\sqrt{1-2a+a^{2}}= a+\sqrt{(1-a)^{2}}= a+1-a= 1$。
乙的解答：$a+\sqrt{1-2a+a^{2}}= a+\sqrt{(a-1)^{2}}= a+a-1= 2a-1= 5$。
哪一个解答是正确的？错误的解答错在哪里？为什么？
乙的解答是正确的，甲的解答错在$\sqrt{(1-a)^{2}}=1-a$。理由如下：
当$a=3$时，$1-a＜0$，所以$\sqrt{(1-a)^{2}}=a-1$。

答案： 解：乙的解答是正确的，甲的解答错在$\sqrt{(1-a)^{2}}=1-a$。理由如下：
当$a=3$时，$1-a＜0$，所以$\sqrt{(1-a)^{2}}=a-1$。

23 运算能力已知$|2024-m|+\sqrt{m-2025}= m$,求$m-2024^{2}$的值。

答案： 解：因为$m-2025≥0$，所以$m≥2025$，
所以$2024-m≤-1$，
所以$|2024-m|+\sqrt{m-2025}=m$可化为$m-2024+\sqrt{m-2025}=m$，
所以$\sqrt{m-2025}=2024$，
所以$m-2025=2024^{2}$，所以$m-2024^{2}=2025$。