《2025年一遍过八年级数学上册北师大版》

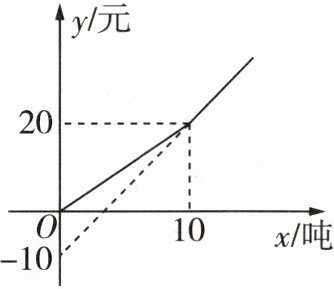
1 [2024泰安泰山区期末]为了提高居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图所示(实线部分)。按上述分段收费标准,小明家六、三月份分别交水费35元和18元,则三月份比六月份节约用水(6吨)

A.3吨
B.4吨
C.5吨
D.6吨

答案： D 当 $ 0 \leq x \leq 10 $ 时，设 $ y = k _ { 1 } x $（$ k _ { 1 } $ 为常数，且 $ k _ { 1 } \neq 0 $），将 $ x = 10 $，$ y = 20 $ 代入 $ y = k _ { 1 } x $，得 $ 10 k _ { 1 } = 20 $，解得 $ k _ { 1 } = 2 $，所以 $ y = 2 x ( 0 \leq x \leq 10 ) $。当 $ x ＞ 10 $ 时，设 $ y = k _ { 2 } x + b $（$ k _ { 2 } $，$ b $ 为常数，且 $ k _ { 2 } \neq 0 $），将 $ x = 0 $，$ y = - 10 $ 和 $ x = 10 $，$ y = 20 $ 代入 $ y = k _ { 2 } x + b $，得 $ b = - 10 $，$ 10 k _ { 2 } + b = 20 $，所以 $ k _ { 2 } = 3 $，所以 $ y = 3 x - 10 ( x ＞ 10 ) $。当 $ y = 35 $ 时，可得 $ 3 x - 10 = 35 $，解得 $ x = 15 $。当 $ y = 18 $ 时，可得 $ 2 x = 18 $，解得 $ x = 9 $。$ 15 - 9 = 6 $（吨），所以三月份比六月份节约用水 6 吨。

2 [2023宜昌中考]某食用油的沸点温度远高于水的沸点温度。小聪想用刻度不超过100℃的温度计测算出这种食用油沸点的温度。在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔10s测量一次锅中油温,得到的数据记录如下：

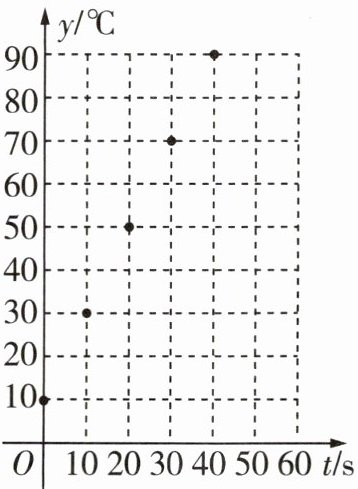
(1)如图,小聪在平面直角坐标系中描出了表中数据对应的点。经老师介绍,在这种食用油达到沸点前,锅中油温y(℃)与加热的时间t(s)符合初中学习过的某种函数关系,填空：可能是____一次____函数关系。
(2)根据以上判断,求y关于t的函数表达式。
解：设锅中油温y关于加热的时间t的函数表达式为y=2t+10。
(3)当加热110s时,油沸腾了,请推算沸点的温度。
解：经过推算，该油的沸点温度是230℃。

答案： 解：
(1)一次
根据表格中两个变量对应值变化的规律可知，时间每增加 $ 10 \mathrm { s } $，油的温度就升高 $ 20 ^ { \circ } \mathrm { C } $，故锅中油温 $ y $ 与加热的时间 $ t $ 可能是一次函数关系。
(2)设锅中油温 $ y $ 关于加热的时间 $ t $ 的函数表达式为 $ y = k t + b ( k \neq 0 ) $，
将点 $ ( 0,10 ) $，$ ( 10,30 ) $ 的坐标代入，得 $ b = 10 $，$ 10 k + b = 30 $，
所以 $ k = 2 $，所以 $ y = 2 t + 10 $。
(3)当 $ t = 110 $ 时，$ y = 2 \times 110 + 10 = 230 $，
所以经过推算，该油的沸点温度是 $ 230 ^ { \circ } \mathrm { C } $。

3 [2024陕西中考]我国新能源汽车快速健康发展,续航里程不断提升。王师傅驾驶一辆纯电动汽车从A市前往B市,他驾车从A市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240km后,从B市一高速公路出口驶出。已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示。
(1)求y与x之间的关系式；
(2)已知这辆车的“满电量”为100kW·h,求王师傅驾车从B市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少。
(1)设 $ y = k x + b ( k \neq 0,0 \leq x \leq 240 ) $，将 $ ( 0,80 ) $，$ ( 150,50 ) $ 代入，得 $ b = 80 $，$ 150 k + b = 50 $，所以 $ k = - \frac { 1 } { 5 } $，所以 $ y $ 与 $ x $ 之间的关系式为 $ y = $$- \frac{1}{5}x + 80$。
(2)令 $ x = 240 $，则 $ y = - \frac { 1 } { 5 } × 240 + 80 = $32，$ \frac { 32 } { 100 } × 100 \% = $32%，所以该车的剩余电量占“满电量”的32%。

答案： 解：
(1)设 $ y = k x + b ( k \neq 0,0 \leq x \leq 240 ) $，将 $ ( 0,80 ) $，$ ( 150,50 ) $ 代入，
得 $ b = 80 $，$ 150 k + b = 50 $，所以 $ k = - \frac { 1 } { 5 } $，
所以 $ y $ 与 $ x $ 之间的关系式为 $ y = - \frac { 1 } { 5 } x + 80 $。
(2)令 $ x = 240 $，则 $ y = - \frac { 1 } { 5 } \times 240 + 80 = 32 $，
$ \frac { 32 } { 100 } \times 100 \% = 32 \% $，
所以该车的剩余电量占“满电量”的 $ 32 \% $。

若x= 4是方程kx + b= 0的解,则直线y= kx + b的图象与x轴交点的坐标为(A)
A.(4,0)
B.(0,4)
C.(0,-4)
D.(-4,0)

答案： A

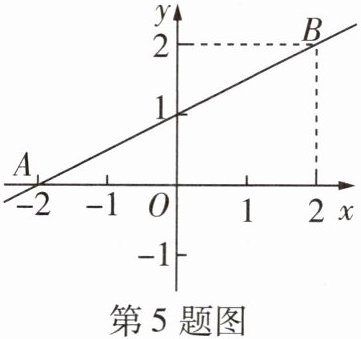
5 [2025郑州冠军中学期中]如图是一次函数y= kx + b的图象,则方程kx + b= 0的解为x=-2。

答案： $ x = - 2 $ 因为一次函数 $ y = k x + b $ 的图象与 $ x $ 轴的交点坐标为 $ ( - 2,0 ) $，所以当 $ x = - 2 $ 时，$ y = 0 $，所以方程 $ k x + b = 0 $ 的解为 $ x = - 2 $。

6 [2024深圳福田区期末]如图,直线y= 2x与y= kx + b相交于点P(m,2),则关于x的方程2x= kx + b的解是____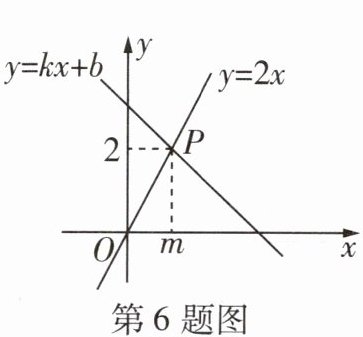x=1。

答案： $ x = 1 $ 因为直线 $ y = 2 x $ 与 $ y = k x + b $ 相交于点 $ P ( m, 2 ) $，所以 $ 2 = 2 m $，所以 $ m = 1 $，所以 $ P ( 1,2 ) $，所以关于 $ x $ 的方程 $ 2 x = k x + b $ 的解是 $ x = 1 $。