第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
8 [2025北京十一学校期中]在平面直角坐标系中,线段AB两端点的坐标分别为A(-1,2),B(2,-3)。作AB关于某直线的对称图形A'B',若B'的坐标为(-2,-3),则A'的坐标为( )
A. (1,2)
B. (2,1)
C. (1,-2)
D. (-1,-2)
A. (1,2)
B. (2,1)
C. (1,-2)
D. (-1,-2)
答案:
8 A 根据题意画出图形,如图,因为 $ B(2,-3) $,$ B'(-2,-3) $,所以点 $ B $ 与点 $ B' $ 关于 $ y $ 轴对称,即线段 $ AB $ 与线段 $ A'B' $ 关于 $ y $ 轴对称,所以 $ A' $ 的坐标为 $ (1,2) $。

8 A 根据题意画出图形,如图,因为 $ B(2,-3) $,$ B'(-2,-3) $,所以点 $ B $ 与点 $ B' $ 关于 $ y $ 轴对称,即线段 $ AB $ 与线段 $ A'B' $ 关于 $ y $ 轴对称,所以 $ A' $ 的坐标为 $ (1,2) $。

9 [2024阜新期末]如果P点的坐标为(a,b),它关于y轴的对称点为$P_1,P_1$关于x轴的对称点为$P_2,$已知$P_2$的坐标为(-2,3),那么点P的坐标为(
A. (-2,-3)
B. (2,-3)
C. (-2,3)
D. (2,3)
(2,-3)
)A. (-2,-3)
B. (2,-3)
C. (-2,3)
D. (2,3)
答案:
9 B 因为 $ P_{2} $ 的坐标为 $ (-2,3) $,$ P_{1} $ 关于 $ x $ 轴的对称点为 $ P_{2} $,所以 $ P_{1}(-2,-3) $,因为 $ P $ 点的坐标为 $ (a,b) $,它关于 $ y $ 轴的对称点为 $ P_{1} $,所以 $ a = 2 $,$ b = -3 $,所以点 $ P $ 的坐标为 $ (2,-3) $。
10 [2025大同新荣区期中]小红同学误将点A的横、纵坐标次序颠倒,写成A(a,b),另一学生误将点B的坐标写成关于y轴的对称点的坐标,写成B(-b,-a),则A,B两点原来的位置关系是(
A. 关于x轴对称
B. 关于y轴对称
C. A和B重合
D. 以上都不对
关于x轴对称
)A. 关于x轴对称
B. 关于y轴对称
C. A和B重合
D. 以上都不对
答案:
10 A 因为小红同学误将点 $ A $ 的横、纵坐标次序颠倒,写成 $ A(a,b) $,所以点 $ A $ 的正确坐标为 $ (b,a) $,因为另一学生误将点 $ B $ 的坐标写成关于 $ y $ 轴的对称点的坐标,写成 $ B(-b,-a) $,所以点 $ B $ 的正确坐标为 $ (b,-a) $,所以 $ A $,$ B $ 两点原来的位置关系是关于 $ x $ 轴对称。
11 [2025江门六校期中联考]如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(1,2),则经过第2025次变换后点A的对应点的坐标为(
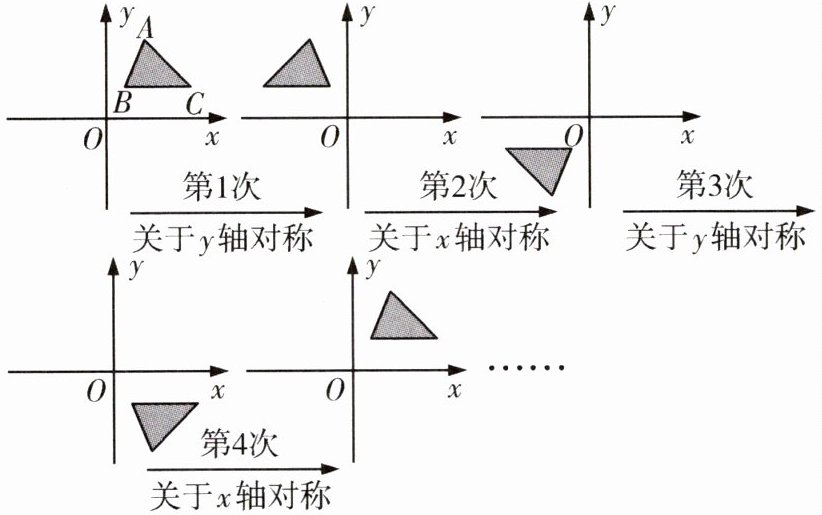
A. (1,-2)
B. (-1,-2)
C. (-1,2)
D. (1,2)
(-1,2)
)
A. (1,-2)
B. (-1,-2)
C. (-1,2)
D. (1,2)
答案:
11 C 点 $ A $ 第 1 次关于 $ y $ 轴对称的对应点的坐标为 $ (-1,2) $,第 2 次关于 $ x $ 轴对称的对应点的坐标为 $ (-1,-2) $,第 3 次关于 $ y $ 轴对称的对应点的坐标为 $ (1,-2) $,第 4 次关于 $ x $ 轴对称的对应点的坐标为 $ (1,2) \cdots \cdots $ 所以每 4 次轴对称变换为一个循环。因为 $ 2025 \div 4 = 506 \cdots \cdots 1 $,所以经过第 2025 次变换后点 $ A $ 的对应点的坐标为 $ (-1,2) $。
12 [2025德阳旌阳区期中]如果点P(2,b)和点Q(a,-3)关于直线x= 1(平行于y轴的直线,直线上的每个点的横坐标都是1)对称,那么a+b的值是
-3
。
答案:
12 $ -3 $
13 [2025昭通期中]如图所示的正方形网格中,每个小正方形的边长都为1,△ABC,△EFD的顶点都在网格线的交点上,在图中建立平面直角坐标系xOy,使△ABC与△EFD关于y轴对称,点C的坐标为(-1,1)。
(1)在图中画出平面直角坐标系xOy;
(2)①写出点B关于x轴的对称点$B_1$的坐标;
②画出△ABC关于x轴对称的图形$△A_1B_1C_1,$其中点A的对称点是$A_1,$点C的对称点是$C_1。$

(1)在图中画出平面直角坐标系xOy;
(2)①写出点B关于x轴的对称点$B_1$的坐标;
②画出△ABC关于x轴对称的图形$△A_1B_1C_1,$其中点A的对称点是$A_1,$点C的对称点是$C_1。$

答案:
13 解:
(1) 建立平面直角坐标系 $ xOy $ 如图所示。

(2) ① $ B_{1}(-4,-2) $。
② $ \triangle A_{1}B_{1}C_{1} $ 如图所示。
13 解:
(1) 建立平面直角坐标系 $ xOy $ 如图所示。

(2) ① $ B_{1}(-4,-2) $。
② $ \triangle A_{1}B_{1}C_{1} $ 如图所示。
14 [2024宁波海曙区四校期中联考]如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,1),C(-2,-2)。
(1)在图中作出△ABC关于y轴对称的图形$△A_1B_1C_1,$并写出$A_1,B_1,C_1$三点的坐标;
(2)在x轴上有一点P,画图找出使得PA+PB取得最小值时点P的位置。(不写作法,保留作图痕迹)
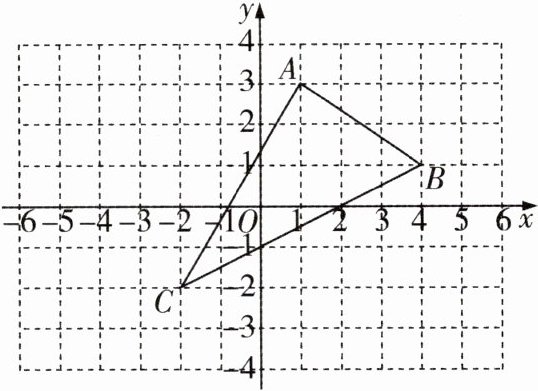
(1)在图中作出△ABC关于y轴对称的图形$△A_1B_1C_1,$并写出$A_1,B_1,C_1$三点的坐标;
(2)在x轴上有一点P,画图找出使得PA+PB取得最小值时点P的位置。(不写作法,保留作图痕迹)

答案:
14 解:
(1) 如图,$ \triangle A_{1}B_{1}C_{1} $ 即所求。点 $ A_{1} $ 的坐标为 $ (-1,3) $,点 $ B_{1} $ 的坐标为 $ (-4,1) $,点 $ C_{1} $ 的坐标为 $ (2,-2) $。

(2) 如图,点 $ P $ 即所求。
作点 $ B $ 关于 $ x $ 轴的对称点 $ B' $,连接 $ AB' $ 交 $ x $ 轴于点 $ P $,点 $ P $ 即所求。
14 解:
(1) 如图,$ \triangle A_{1}B_{1}C_{1} $ 即所求。点 $ A_{1} $ 的坐标为 $ (-1,3) $,点 $ B_{1} $ 的坐标为 $ (-4,1) $,点 $ C_{1} $ 的坐标为 $ (2,-2) $。

(2) 如图,点 $ P $ 即所求。
作点 $ B $ 关于 $ x $ 轴的对称点 $ B' $,连接 $ AB' $ 交 $ x $ 轴于点 $ P $,点 $ P $ 即所求。
查看更多完整答案,请扫码查看


