第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
9 [2024烟台福山区质检]给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有$a^{2}+b^{2}= c^{2}$;
④若三个整数a,b,c(c最大)是直角三角形的三边长,则2a,2b,2c一定是勾股数。
其中正确的是 (
A. ①②
B. ②③
C. ③④
D. ①④
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有$a^{2}+b^{2}= c^{2}$;
④若三个整数a,b,c(c最大)是直角三角形的三边长,则2a,2b,2c一定是勾股数。
其中正确的是 (
③④
)A. ①②
B. ②③
C. ③④
D. ①④
答案:
C 由于0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,但是0.3² + 0.4² = 0.5²,所以以0.3,0.4,0.5为边长的三角形是直角三角形,故①说法错误;虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;若a,b,c是勾股数,且c最大,则一定有a² + b² = c²,故③说法正确;若三个整数a,b,c(c最大)是直角三角形的三边长,则a² + b² = c²,所以(2a)² + (2b)² = (2c)²,所以2a,2b,2c一定是勾股数,故④说法正确。
10 [2024西安曲江一中期末]如图,在$4×4$的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则下列结论错误的是 (
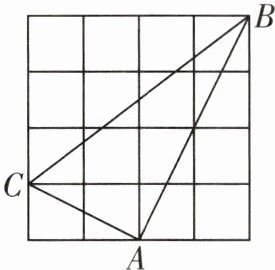
A. $AB^{2}= 20$
B. $∠BAC= 90^{\circ}$
C. $\triangle ABC$的面积为10
D. 点A到直线BC的距离是2
C
)
A. $AB^{2}= 20$
B. $∠BAC= 90^{\circ}$
C. $\triangle ABC$的面积为10
D. 点A到直线BC的距离是2
答案:
C A项,AB² = 2² + 4² = 20,结论正确,不符合题意;B项,因为AC² = 1² + 2² = 5,AB² = 2² + 4² = 20,BC² = 3² + 4² = 25,所以AC² + AB² = BC²,所以∠BAC = 90°,结论正确,不符合题意;C项,S△ABC = 4 × 4 - $\frac{1}{2}$ × 3 × 4 - $\frac{1}{2}$ × 1 × 2 - $\frac{1}{2}$ × 2 × 4 = 5,结论错误,符合题意;D项,设点A到直线BC的距离为h,因为BC² = 3² + 4² = 25,所以BC = 5,则$\frac{1}{2}$ × 5 × h = 5,解得h = 2,即点A到直线BC的距离是2,结论正确,不符合题意。
11 天星原创 如图,分别以$\triangle ABC$的三边为边向外作正方形,然后分别以三个正方形的中心为圆心,以正方形边长的一半为半径作圆,记三个圆的面积分别为$S_{1}$,$S_{2}$,$S_{3}$,若$S_{1}+S_{2}= S_{3}$,则$\triangle ABC$为
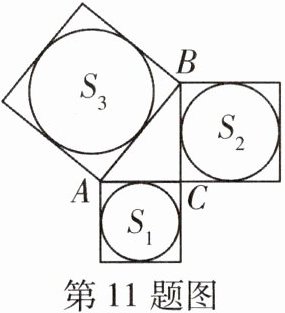
直角
三角形。
答案:
直角 由题意,得S₁ = π($\frac{1}{2}$AC)² = $\frac{1}{4}$πAC²,S₂ = π($\frac{1}{2}$BC)² = $\frac{1}{4}$πBC²,S₃ = π($\frac{1}{2}$AB)² = $\frac{1}{4}$πAB²。因为S₁ + S₂ = S₃,即$\frac{1}{4}$πAC² + $\frac{1}{4}$πBC² = $\frac{1}{4}$πAB²,所以AC² + BC² = AB²,所以△ABC为直角三角形。
12 [2024江门蓬江区月考]如图所示的一块地,$AD= 12m$,$CD= 9m$,$∠ADC= 90^{\circ}$,$AB= 39m$,$BC= 36m$,这块地的面积为____。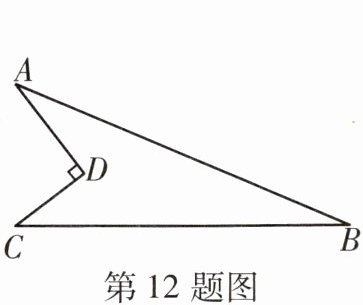

答案:
216 m² 如图,连接AC。在Rt△ADC中,由勾股定理,得AC² = CD² + AD² = 9² + 12² = 225,所以AC = 15m。在△ABC中,AB² = 1521,AC² + BC² = 15² + 36² = 1521,所以AB² = AC² + BC²,所以∠ACB = 90°,所以这块地的面积为S△ABC - S△ACD = $\frac{1}{2}$AC · BC - $\frac{1}{2}$AD · CD = $\frac{1}{2}$ × 15 × 36 - $\frac{1}{2}$ × 12 × 9 = 270 - 54 = 216(m²)。

名师点睛
一般情况下,求不规则图形的面积,通常可通过作辅助线将该图形转化为规则图形进行计算,如本题通过连接AC,将这块地的面积转化为两个直角三角形面积的差。
216 m² 如图,连接AC。在Rt△ADC中,由勾股定理,得AC² = CD² + AD² = 9² + 12² = 225,所以AC = 15m。在△ABC中,AB² = 1521,AC² + BC² = 15² + 36² = 1521,所以AB² = AC² + BC²,所以∠ACB = 90°,所以这块地的面积为S△ABC - S△ACD = $\frac{1}{2}$AC · BC - $\frac{1}{2}$AD · CD = $\frac{1}{2}$ × 15 × 36 - $\frac{1}{2}$ × 12 × 9 = 270 - 54 = 216(m²)。

名师点睛
一般情况下,求不规则图形的面积,通常可通过作辅助线将该图形转化为规则图形进行计算,如本题通过连接AC,将这块地的面积转化为两个直角三角形面积的差。
13 [2025郑州期中]如图,点D是$\triangle ABC$边BC的中点,过点D作$DE⊥BC$交AB于点E,$BD= 5$,$DE= \frac{15}{4}$,$AE= \frac{7}{4}$,$AC= 6$,$\triangle ABC$是直角三角形吗?请通过计算说明理由。
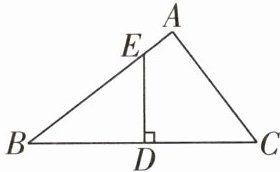

答案:
解:△ABC是直角三角形。理由如下:
如图,连接CE,
因为DE⊥BC,所以∠BDE = 90°,
在Rt△BDE中,BD = 5,DE = $\frac{15}{4}$,由勾股定理,得BE = $\frac{25}{4}$,
因为点D是△ABC边BC的中点,DE⊥BC,
所以DE是线段BC的垂直平分线,所以CE = BE = $\frac{25}{4}$,
因为CE² = ($\frac{25}{4}$)² = $\frac{625}{16}$,AE² = ($\frac{7}{4}$)² = $\frac{49}{16}$,AC² = 6² = 36,$\frac{625}{16}$ - $\frac{49}{16}$ = 36,所以CE² = AE² + AC²,所以∠A = 90°,
所以△ABC是直角三角形。

解:△ABC是直角三角形。理由如下:
如图,连接CE,
因为DE⊥BC,所以∠BDE = 90°,
在Rt△BDE中,BD = 5,DE = $\frac{15}{4}$,由勾股定理,得BE = $\frac{25}{4}$,
因为点D是△ABC边BC的中点,DE⊥BC,
所以DE是线段BC的垂直平分线,所以CE = BE = $\frac{25}{4}$,
因为CE² = ($\frac{25}{4}$)² = $\frac{625}{16}$,AE² = ($\frac{7}{4}$)² = $\frac{49}{16}$,AC² = 6² = 36,$\frac{625}{16}$ - $\frac{49}{16}$ = 36,所以CE² = AE² + AC²,所以∠A = 90°,
所以△ABC是直角三角形。

14 推理能力[2025成都锦江区月考]满足$a^{2}+b^{2}= c^{2}$的三个正整数,称为勾股数。
(1)请把下列三组勾股数补充完整:①
(2)小明发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成$m^{2}+n^{2}$,$m^{2}-n^{2}$,如$4= 2×2×1$,$5= 2^{2}+1^{2}$,$3= 2^{2}-1^{2}$,请你帮小明说明这三个数2mn,$m^{2}+n^{2}$,$m^{2}-n^{2}$是勾股数组。
(3)如果28,96,100是满足上述小明发现的规律的勾股数组,那么$m+n= $
(1)请把下列三组勾股数补充完整:①
6
,8,10;②9,12
,15;③9,40,41
。(2)小明发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成$m^{2}+n^{2}$,$m^{2}-n^{2}$,如$4= 2×2×1$,$5= 2^{2}+1^{2}$,$3= 2^{2}-1^{2}$,请你帮小明说明这三个数2mn,$m^{2}+n^{2}$,$m^{2}-n^{2}$是勾股数组。
(3)如果28,96,100是满足上述小明发现的规律的勾股数组,那么$m+n= $
7
。
答案:
解:
(1)6 12 41
(2)(2mn)² = 4m²n²,(m² + n²)² = m⁴ + 2m²n² + n⁴,(m² - n²)² = m⁴ - 2m²n² + n⁴,
显然,m⁴ + 2m²n² + n⁴ = m⁴ - 2m²n² + n⁴ + 4m²n²,
即(m² + n²)² = (m² - n²)² + (2mn)²,
所以2mn,m² + n²,m² - n²是勾数组。
(3)7
28,96,100约去公因数4,得到7,24,25,其中24 = 2 × 3 × 4,因为25 = 4² + 3²,7 = 4² - 3²,所以m = 4,n = 3,所以m + n = 7。
(1)6 12 41
(2)(2mn)² = 4m²n²,(m² + n²)² = m⁴ + 2m²n² + n⁴,(m² - n²)² = m⁴ - 2m²n² + n⁴,
显然,m⁴ + 2m²n² + n⁴ = m⁴ - 2m²n² + n⁴ + 4m²n²,
即(m² + n²)² = (m² - n²)² + (2mn)²,
所以2mn,m² + n²,m² - n²是勾数组。
(3)7
28,96,100约去公因数4,得到7,24,25,其中24 = 2 × 3 × 4,因为25 = 4² + 3²,7 = 4² - 3²,所以m = 4,n = 3,所以m + n = 7。
查看更多完整答案,请扫码查看


