第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
已知关于x的一次函数$y= (m-1)x+7-3m$。
【基础设问】
(1)当m满足什么条件时,它的图象经过原点?
(2)当m满足什么条件时,它的图象平行于直线$y= -x+8$?
(3)当m满足什么条件时,y随x的增大而减小?
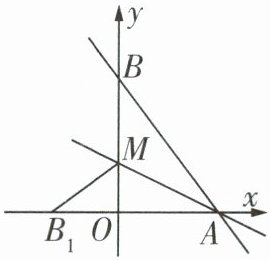
(4)若$m= -\frac {1}{3}$,如图,一次函数的图象分别交x轴、y轴于点A,B,M是OB上一点,若将$\triangle ABM$沿直线AM折叠,使点B恰好落在x轴上的点$B_{1}$处。
①求A,B两点的坐标及$\triangle AOB$的面积。
②一次函数的图象经过第
③点$(-3,4)$
④求直线AM的函数表达式。
【能力设问】
(5)在(4)条件下,若一次函数的图象平移后与x轴、y轴分别交于P,Q两点,且$BA= PA$,求点P的坐标和直线PQ的函数表达式。
【拓展设问】
(6)在(4)条件下,过$\triangle AOB的顶点能否画出直线把\triangle AOB$分成面积相等的两部分? 若能,可以画几条? 并求出满足条件的直线的函数表达式;若不能,请说明理由。
【基础设问】
(1)当m满足什么条件时,它的图象经过原点?
(2)当m满足什么条件时,它的图象平行于直线$y= -x+8$?
(3)当m满足什么条件时,y随x的增大而减小?
(4)若$m= -\frac {1}{3}$,如图,一次函数的图象分别交x轴、y轴于点A,B,M是OB上一点,若将$\triangle ABM$沿直线AM折叠,使点B恰好落在x轴上的点$B_{1}$处。
①求A,B两点的坐标及$\triangle AOB$的面积。
②一次函数的图象经过第
一、二、四
象限。③点$(-3,4)$
不在
(填“在”或“不在”)该一次函数图象上。④求直线AM的函数表达式。
【能力设问】
(5)在(4)条件下,若一次函数的图象平移后与x轴、y轴分别交于P,Q两点,且$BA= PA$,求点P的坐标和直线PQ的函数表达式。
【拓展设问】
(6)在(4)条件下,过$\triangle AOB的顶点能否画出直线把\triangle AOB$分成面积相等的两部分? 若能,可以画几条? 并求出满足条件的直线的函数表达式;若不能,请说明理由。

答案:
解:
(1)因为一次函数的图象经过原点,
所以 $7 - 3m = 0$,且 $m - 1 \neq 0$,所以 $m = \frac{7}{3}$。
(2)因为一次函数的图象平行于直线 $y = -x + 8$,
所以 $m - 1 = -1$,且 $7 - 3m \neq 8$,所以 $m = 0$。
(3)因为一次函数 $y = (m - 1)x + 7 - 3m$ 中,$y$ 随 $x$ 的增大而减小,所以 $m - 1 < 0$,所以 $m < 1$。
(4)①当 $m = -\frac{1}{3}$ 时,一次函数的表达式为 $y = -\frac{4}{3}x + 8$。
令 $x = 0$,得 $y = -\frac{4}{3}x + 8 = 8$,所以点 $B$ 的坐标为 $(0, 8)$。
令 $y = -\frac{4}{3}x + 8 = 0$,解得 $x = 6$,所以点 $A$ 的坐标为 $(6, 0)$,
所以 $OB = 8$,$OA = 6$,所以 $\triangle ABO$ 的面积为 $\frac{1}{2} \times OA \times OB = 24$。
②一、二、四
③不在
④由折叠和勾股定理得,$AB_1 = AB = 10$,
所以 $OB_1 = AB_1 - OA = 10 - 6 = 4$。
设 $MO = x$,则 $MB = MB_1 = 8 - x$。
在 $Rt\triangle OMB_1$ 中,$OM^2 + OB_1^2 = B_1M^2$,
即 $x^2 + 4^2 = (8 - x)^2$,解得 $x = 3$,所以点 $M(0, 3)$。
设直线 $AM$ 的函数表达式为 $y = kx + b$,
把 $(0, 3)$ 代入,得 $b = 3$,
把 $(6, 0)$ 代入,得 $6k + 3 = 0$,所以 $k = -\frac{1}{2}$,
所以直线 $AM$ 的函数表达式为 $y = -\frac{1}{2}x + 3$。
(5)因为点 $A(6, 0)$,点 $B(0, 8)$,$AB = 10$,$BA = PA$,
所以点 $P$ 的坐标为 $(-4, 0)$ 或 $(16, 0)$。
由题意可设直线 $PQ$ 的函数表达式为 $y = -\frac{4}{3}x + c$,
当点 $P$ 的坐标为 $(-4, 0)$ 时,$0 = -\frac{4}{3} \times (-4) + c$,
解得 $c = -\frac{16}{3}$;
当点 $P$ 的坐标为 $(16, 0)$ 时,$0 = -\frac{4}{3} \times 16 + c$,
解得 $c = \frac{64}{3}$。
所以直线 $PQ$ 的函数表达式为 $y = -\frac{4}{3}x - \frac{16}{3}$ 或 $y = -\frac{4}{3}x + \frac{64}{3}$。
(6)能画出三条。
因为 $A(6, 0)$,$B(0, 8)$,$O(0, 0)$,设 $AB$ 的中点为 $D$,$OA$ 的中点为 $E$,$OB$ 的中点为 $F$,所以 $D(3, 4)$,$E(3, 0)$,$F(0, 4)$。
把 $\triangle AOB$ 分成面积相等的两部分的直线有以下三条:
$1^{\circ}$ 当所画直线过点 $O$,$D$ 时,
设直线 $OD$ 的函数表达式为 $y = k_1x$,
将 $D(3, 4)$ 的坐标代入,得 $4 = 3k_1$,解得 $k_1 = \frac{4}{3}$,
所以直线 $OD$ 的函数表达式为 $y = \frac{4}{3}x$。
$2^{\circ}$ 当所画直线过点 $B$,$E$ 时,
设直线 $BE$ 的函数表达式为 $y = px + 8$,
将 $E(3, 0)$ 的坐标代入,得 $0 = 3p + 8$,解得 $p = -\frac{8}{3}$,
所以直线 $BE$ 的函数表达式为 $y = -\frac{8}{3}x + 8$。
$3^{\circ}$ 当所画直线过点 $A$,$F$ 时,
设直线 $AF$ 的函数表达式为 $y = qx + 4$,
将 $A(6, 0)$ 的坐标代入,得 $0 = 6q + 4$,解得 $q = -\frac{2}{3}$,
所以直线 $AF$ 的函数表达式为 $y = -\frac{2}{3}x + 4$。
(1)因为一次函数的图象经过原点,
所以 $7 - 3m = 0$,且 $m - 1 \neq 0$,所以 $m = \frac{7}{3}$。
(2)因为一次函数的图象平行于直线 $y = -x + 8$,
所以 $m - 1 = -1$,且 $7 - 3m \neq 8$,所以 $m = 0$。
(3)因为一次函数 $y = (m - 1)x + 7 - 3m$ 中,$y$ 随 $x$ 的增大而减小,所以 $m - 1 < 0$,所以 $m < 1$。
(4)①当 $m = -\frac{1}{3}$ 时,一次函数的表达式为 $y = -\frac{4}{3}x + 8$。
令 $x = 0$,得 $y = -\frac{4}{3}x + 8 = 8$,所以点 $B$ 的坐标为 $(0, 8)$。
令 $y = -\frac{4}{3}x + 8 = 0$,解得 $x = 6$,所以点 $A$ 的坐标为 $(6, 0)$,
所以 $OB = 8$,$OA = 6$,所以 $\triangle ABO$ 的面积为 $\frac{1}{2} \times OA \times OB = 24$。
②一、二、四
③不在
④由折叠和勾股定理得,$AB_1 = AB = 10$,
所以 $OB_1 = AB_1 - OA = 10 - 6 = 4$。
设 $MO = x$,则 $MB = MB_1 = 8 - x$。
在 $Rt\triangle OMB_1$ 中,$OM^2 + OB_1^2 = B_1M^2$,
即 $x^2 + 4^2 = (8 - x)^2$,解得 $x = 3$,所以点 $M(0, 3)$。
设直线 $AM$ 的函数表达式为 $y = kx + b$,
把 $(0, 3)$ 代入,得 $b = 3$,
把 $(6, 0)$ 代入,得 $6k + 3 = 0$,所以 $k = -\frac{1}{2}$,
所以直线 $AM$ 的函数表达式为 $y = -\frac{1}{2}x + 3$。
(5)因为点 $A(6, 0)$,点 $B(0, 8)$,$AB = 10$,$BA = PA$,
所以点 $P$ 的坐标为 $(-4, 0)$ 或 $(16, 0)$。
由题意可设直线 $PQ$ 的函数表达式为 $y = -\frac{4}{3}x + c$,
当点 $P$ 的坐标为 $(-4, 0)$ 时,$0 = -\frac{4}{3} \times (-4) + c$,
解得 $c = -\frac{16}{3}$;
当点 $P$ 的坐标为 $(16, 0)$ 时,$0 = -\frac{4}{3} \times 16 + c$,
解得 $c = \frac{64}{3}$。
所以直线 $PQ$ 的函数表达式为 $y = -\frac{4}{3}x - \frac{16}{3}$ 或 $y = -\frac{4}{3}x + \frac{64}{3}$。
(6)能画出三条。
因为 $A(6, 0)$,$B(0, 8)$,$O(0, 0)$,设 $AB$ 的中点为 $D$,$OA$ 的中点为 $E$,$OB$ 的中点为 $F$,所以 $D(3, 4)$,$E(3, 0)$,$F(0, 4)$。
把 $\triangle AOB$ 分成面积相等的两部分的直线有以下三条:
$1^{\circ}$ 当所画直线过点 $O$,$D$ 时,
设直线 $OD$ 的函数表达式为 $y = k_1x$,
将 $D(3, 4)$ 的坐标代入,得 $4 = 3k_1$,解得 $k_1 = \frac{4}{3}$,
所以直线 $OD$ 的函数表达式为 $y = \frac{4}{3}x$。
$2^{\circ}$ 当所画直线过点 $B$,$E$ 时,
设直线 $BE$ 的函数表达式为 $y = px + 8$,
将 $E(3, 0)$ 的坐标代入,得 $0 = 3p + 8$,解得 $p = -\frac{8}{3}$,
所以直线 $BE$ 的函数表达式为 $y = -\frac{8}{3}x + 8$。
$3^{\circ}$ 当所画直线过点 $A$,$F$ 时,
设直线 $AF$ 的函数表达式为 $y = qx + 4$,
将 $A(6, 0)$ 的坐标代入,得 $0 = 6q + 4$,解得 $q = -\frac{2}{3}$,
所以直线 $AF$ 的函数表达式为 $y = -\frac{2}{3}x + 4$。
查看更多完整答案,请扫码查看


