第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
8 [2024揭阳期末]在$Rt\triangle ABC$中,$AB^{2}= 9,AC^{2}= 25$,则$BC^{2}=$(
A. 16
B. 4或34
C. 16或34
D. 4或24
16或34
)A. 16
B. 4或34
C. 16或34
D. 4或24
答案:
C 当∠B=90°时,BC²=AC²-AB²=25-9=16;当∠A=90°时,BC²=AB²+AC²=9+25=34。
归纳总结
已知直角三角形两边长求第三边长的策略
若题目中明确给出斜边长和一条直角边长(或给出两条直角边长),则直接运用勾股定理求解;若题目中没有明确说明给出的边长是直角边长还是斜边长,则要运用分类讨论的思想,分情况进行求解,且要注意验证。
归纳总结
已知直角三角形两边长求第三边长的策略
若题目中明确给出斜边长和一条直角边长(或给出两条直角边长),则直接运用勾股定理求解;若题目中没有明确说明给出的边长是直角边长还是斜边长,则要运用分类讨论的思想,分情况进行求解,且要注意验证。
9 [2025梅州期末]小明将一张长为20cm、宽为15cm的长方形纸片$(AE>DE)$剪去了一角,剩余部分如图所示,量得$AB= 3cm,CD= 4cm$,则剪去的直角三角形的斜边长为( )

A. 5cm
B. 12cm
C. 16cm
D. 20cm

A. 5cm
B. 12cm
C. 16cm
D. 20cm
答案:
D 如图,延长AB,DC相交于点F,则△BFC是直角三角形,根据勾股定理,得BC²=BF²+FC²=(15-3)²+(20-4)²=12²+16²=400,所以BC=20cm,故剪去的直角三角形的斜边长为20cm。

D 如图,延长AB,DC相交于点F,则△BFC是直角三角形,根据勾股定理,得BC²=BF²+FC²=(15-3)²+(20-4)²=12²+16²=400,所以BC=20cm,故剪去的直角三角形的斜边长为20cm。

10 [教材习题变式][2025郑州枫杨外国语学校月考]如图,在$Rt\triangle ABC$中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为$S_{1},S_{2},S_{3}$。若$S_{3}+S_{2}-S_{1}= 18$。则图中阴影部分的面积为(
A. 6
B. $\frac{9}{2}$
C. 5
D. $\frac{7}{2}$
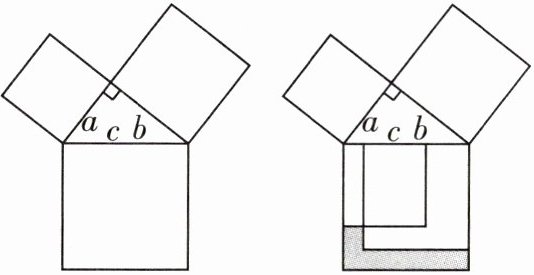
[变式][2025南宁三美学校月考]勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载。勾股定理描述:直角三角形两条直角边的平方和等于斜边的平方。如图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图中的方式放置在最大正方形内。则图中阴影部分的面积为(
A. $\frac{(a+b)^{2}-c^{2}}{4}$
B. $b^{2}-a^{2}$
C. $a(a+b-c)$
D. $c^{2}-\frac{1}{2}ab$
B
)
A. 6
B. $\frac{9}{2}$
C. 5
D. $\frac{7}{2}$
[变式][2025南宁三美学校月考]勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载。勾股定理描述:直角三角形两条直角边的平方和等于斜边的平方。如图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图中的方式放置在最大正方形内。则图中阴影部分的面积为(
C
)
A. $\frac{(a+b)^{2}-c^{2}}{4}$
B. $b^{2}-a^{2}$
C. $a(a+b-c)$
D. $c^{2}-\frac{1}{2}ab$
答案:
B 在Rt△ABC中,由勾股定理,得AC²+AB²=BC²,所以S₁+S₂=S₃,因为S₃+S₂-S₁=18,所以S₂=9,由题中图形可知,阴影部分的面积为$\frac{1}{2}S₂,$所以阴影部分的面积为$\frac{9}{2}。$
变式 C 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图中的方式放置在最大正方形内,则阴影部分面积=大正方形面积-两个小正方形面积+重叠部分面积。由勾股定理,得大正方形面积等于两个小正方形面积和,重叠部分为一个长方形,所以阴影部分面积与重叠部分面积相等,因为重叠部分的长为a,宽为a+b-c,所以阴影部分面积=重叠部分面积=a(a+b-c)。
变式 C 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图中的方式放置在最大正方形内,则阴影部分面积=大正方形面积-两个小正方形面积+重叠部分面积。由勾股定理,得大正方形面积等于两个小正方形面积和,重叠部分为一个长方形,所以阴影部分面积与重叠部分面积相等,因为重叠部分的长为a,宽为a+b-c,所以阴影部分面积=重叠部分面积=a(a+b-c)。
11 [新趋势·数学文化][2025无锡期末]我国古代称直角三角形为“勾股形”。如图,数学家刘徽(约公元225年~公元295年)将勾股形分割成一个正方形和两对全等的直角三角形。若$a= 10,b= 2$,则此勾股形的面积为( )

A. 28
B. 30
C. 32
D. 36

A. 28
B. 30
C. 32
D. 36
答案:
B 设阴影部分的直角三角形的未知直角边长为x,如图,则BC=x+b,AC=x+a,BA=a+b,由勾股定理,得(x+b)²+(a+b)²=(x+a)²。因为a=10,b=2,所以(x+2)²+(10+2)²=(x+10)²,所以x=3,所以BC=3+2=5,AB=10+2=12,所以△ABC的面积为$\frac{1}{2}×12×5=30。$

B 设阴影部分的直角三角形的未知直角边长为x,如图,则BC=x+b,AC=x+a,BA=a+b,由勾股定理,得(x+b)²+(a+b)²=(x+a)²。因为a=10,b=2,所以(x+2)²+(10+2)²=(x+10)²,所以x=3,所以BC=3+2=5,AB=10+2=12,所以△ABC的面积为$\frac{1}{2}×12×5=30。$

12 [教材习题变式]如图,在$\triangle ABC$中,$BC= 13,AB= 14,AC= 15$,则$\triangle ABC$的面积为____。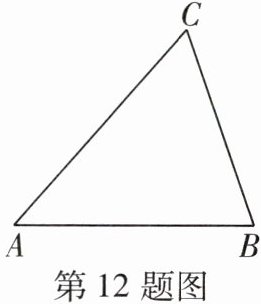

答案:
84 如图,过点C作CD⊥AB于点D,则∠ADC=∠BDC=90°,所以AC²-AD²=BC²-BD²=CD²,所以15²-AD²=13²-(14-AD)²,所以AD=9,所以CD²=AC²-AD²=144,所以CD=12,所以△ABC的面积为$\frac{1}{2}AB·CD= \frac{1}{2}×14×12=84。$
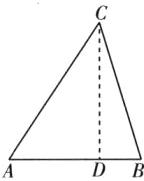
策略点拨
构造直角三角形法
当题目中没有直角三角形时,往往先通过作垂线(或作高线)构造直角三角形,然后利用勾股定理求得线段的长。需要注意的是构造直角三角形时,不能破坏已知条件中的特殊角和边。
84 如图,过点C作CD⊥AB于点D,则∠ADC=∠BDC=90°,所以AC²-AD²=BC²-BD²=CD²,所以15²-AD²=13²-(14-AD)²,所以AD=9,所以CD²=AC²-AD²=144,所以CD=12,所以△ABC的面积为$\frac{1}{2}AB·CD= \frac{1}{2}×14×12=84。$

策略点拨
构造直角三角形法
当题目中没有直角三角形时,往往先通过作垂线(或作高线)构造直角三角形,然后利用勾股定理求得线段的长。需要注意的是构造直角三角形时,不能破坏已知条件中的特殊角和边。
13 [2024沈阳期末]如图,在$\triangle ABC$中,$∠C= 90^{\circ }$,M是BC的中点,$MD⊥AB$于点D,若$AC= 2cm,AD= \frac{5}{2}cm$,则BD的长度为____cm。


答案:
$\frac{3}{2} $如图,连接AM,因为M是BC的中点,MD⊥AB,∠C=90°,所以AM²=AD²+DM²=AC²+CM²,CM²=BM²=BD²+DM²,所以AD²=AC²+BD²,因为AC=2cm,$AD= \frac{5}{2}cm,$所以$BD²=AD²-AC²= \frac{9}{4},$所以$BD= \frac{3}{2}cm。$

$\frac{3}{2} $如图,连接AM,因为M是BC的中点,MD⊥AB,∠C=90°,所以AM²=AD²+DM²=AC²+CM²,CM²=BM²=BD²+DM²,所以AD²=AC²+BD²,因为AC=2cm,$AD= \frac{5}{2}cm,$所以$BD²=AD²-AC²= \frac{9}{4},$所以$BD= \frac{3}{2}cm。$

14 [几何直观][2024汕头潮南区期中]已知:如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },AB= 5,AC= 3$,动点P从点B出发沿射线BC以每秒1个单位长度的速度移动,设运动的时间为t秒。
(1)$BC= $____,AB边上的高$h= $____;
(2)当$\triangle ABP$为直角三角形时,求t的值。

(1)$BC= $____,AB边上的高$h= $____;
(2)当$\triangle ABP$为直角三角形时,求t的值。

答案:
解:$(1)4 \frac{12}{5}$在Rt△ABC中,∠ACB=90°,AB=5,AC=3,所以BC=4,因为$S_{△ABC}= \frac{1}{2}AB·h= \frac{1}{2}AC·BC,$所以$h= \frac{AC·BC}{AB}= \frac{3×4}{5}= \frac{12}{5}。$
(2)由题意,得BP=t,在Rt△ABP中,∠B为锐角,当∠APB=90°时,BP=BC,此时t=4;当∠BAP=90°时,如图,则CP=t-4,在Rt△APC中,AP²=AC²+CP²=3²+(t-4)²,在Rt△ABP中,AP²+AB²=BP²,所以3²+(t-4)²+5²=t²,解得$t= \frac{25}{4}。$
综上所述,t的值为4或$\frac{25}{4}。$

解:$(1)4 \frac{12}{5}$在Rt△ABC中,∠ACB=90°,AB=5,AC=3,所以BC=4,因为$S_{△ABC}= \frac{1}{2}AB·h= \frac{1}{2}AC·BC,$所以$h= \frac{AC·BC}{AB}= \frac{3×4}{5}= \frac{12}{5}。$
(2)由题意,得BP=t,在Rt△ABP中,∠B为锐角,当∠APB=90°时,BP=BC,此时t=4;当∠BAP=90°时,如图,则CP=t-4,在Rt△APC中,AP²=AC²+CP²=3²+(t-4)²,在Rt△ABP中,AP²+AB²=BP²,所以3²+(t-4)²+5²=t²,解得$t= \frac{25}{4}。$
综上所述,t的值为4或$\frac{25}{4}。$

查看更多完整答案,请扫码查看


