第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
10 [2025上海南汇实验学校期中]下列说法中正确的有 (
①$y= kx$是正比例函数;
②如果$y= (a+3)x+a^{2}-9$是正比例函数,那么$a= \pm 3$;
③如果y与$x+2$成正比例,那么y是x的正比例函数;
④如果$y= \frac {1}{3}x^{2}$,那么y与$x^{2}$成正比例。
A.4个
B.3个
C.2个
D.1个
④
)①$y= kx$是正比例函数;
②如果$y= (a+3)x+a^{2}-9$是正比例函数,那么$a= \pm 3$;
③如果y与$x+2$成正比例,那么y是x的正比例函数;
④如果$y= \frac {1}{3}x^{2}$,那么y与$x^{2}$成正比例。
A.4个
B.3个
C.2个
D.1个
答案:
D ①当 $ k \neq 0 $ 时,$ y = k x $ 是正比例函数,原说法错误,不符合题意;②如果 $ y = ( a + 3 ) x + a ^ { 2 } - 9 $ 是正比例函数,那么 $ a = 3 $,原说法错误,不符合题意;③如果 $ y $ 与 $ x + 2 $ 成正比例,那么 $ y = k ( x + 2 ) $ 不是 $ x $ 的正比例函数,原说法错误,不符合题意;④如果 $ y = \frac { 1 } { 3 } x ^ { 2 } $,那么 $ y $ 与 $ x ^ { 2 } $ 成正比例,说法正确,符合题意。
11 [2025南京外国语学校月考]李大爷要围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长恰好为24米。若要围成的菜园是如图所示的长方形ABCD,设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是 (

A.$y= -2x+24(0\lt x\lt 12)$
B.$y= -\frac {1}{2}x+12(0\lt x\lt 24)$
C.$y= 2x-24(0\lt x\lt 12)$
D.$y= \frac {1}{2}x-12(0\lt x\lt 24)$
$ y = - \frac { 1 } { 2 } x + 12 $($ 0 < x < 24 $)
)
A.$y= -2x+24(0\lt x\lt 12)$
B.$y= -\frac {1}{2}x+12(0\lt x\lt 24)$
C.$y= 2x-24(0\lt x\lt 12)$
D.$y= \frac {1}{2}x-12(0\lt x\lt 24)$
答案:
B 由题意得,$ 2 y + x = 24 $,所以 $ y = - \frac { 1 } { 2 } x + 12 $($ 0 < x < 24 $)。
12 [2024惠州期末]已知摄氏温度$x(^{\circ }C)与华氏温度y(^{\circ }F)$之间存在如下关系:

根据表中提供的信息,则y与x之间的函数关系式为

根据表中提供的信息,则y与x之间的函数关系式为
$ y = 1.8 x + 32 $
。
答案:
$ y = 1.8 x + 32 $
13 新定义:$[a,b]为一次函数y= ax+b$(a,b为常数,$a≠0$)的“联盟数”。若“联盟数”为$[1,m-5]$的一次函数是正比例函数,则m的值为____
5
。
答案:
5 由题意知,“联盟数”为 $ [ 1 , m - 5 ] $ 的一次函数是 $ y = x + m - 5 $,因为“联盟数”为 $ [ 1 , m - 5 ] $ 的一次函数是正比例函数,所以 $ m - 5 = 0 $,所以 $ m = 5 $。
14 教材例题变式 [2025烟台期末]海水养殖是烟台经济产业的亮丽名片之一。某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了300万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不符合要求,最后只能按照20元一笼出售,如果纯收入为y万元,不符合要求的扇贝有x万笼。
(1)求y关于x的关系式。
(2)当符合要求的扇贝有多少笼时,养殖场不赔不赚?
(1)求y关于x的关系式。
(2)当符合要求的扇贝有多少笼时,养殖场不赔不赚?
答案:
解:
(1)由题意,得 $ y = ( 100 - 40 ) ( 300 - x ) + ( 20 - 40 ) x = 60 ( 300 - x ) - 20 x = - 80 x + 18000 $,所以 $ y $ 关于 $ x $ 的关系式为 $ y = - 80 x + 18000 $。
(2)当养殖场不赔不赚时 $ y = 0 $,解方程 $ 0 = - 80 x + 18000 $,得 $ x = 225 $,所以 $ 300 - x = 300 - 225 = 75 $,所以当符合要求的扇贝有 75 万笼时,养殖场不赔不赚。
(1)由题意,得 $ y = ( 100 - 40 ) ( 300 - x ) + ( 20 - 40 ) x = 60 ( 300 - x ) - 20 x = - 80 x + 18000 $,所以 $ y $ 关于 $ x $ 的关系式为 $ y = - 80 x + 18000 $。
(2)当养殖场不赔不赚时 $ y = 0 $,解方程 $ 0 = - 80 x + 18000 $,得 $ x = 225 $,所以 $ 300 - x = 300 - 225 = 75 $,所以当符合要求的扇贝有 75 万笼时,养殖场不赔不赚。
15 抽象能力 如图,已知长方形ABCD中,$AB= CD= 16,BC= DA= 24$,E为CD边的中点,P为长方形ABCD边上的动点,动点P以4个单位/秒的速度从点A出发,沿着$A→B→C→E$运动到点E停止。设点P运动的时间为t秒,$\triangle APE$的面积为y。
(1)当$t= 2$时,y的值是____;当$t= 6$时,y的值是____。
(2)直接写出在点P的运动过程中,y与t之间的函数关系式。
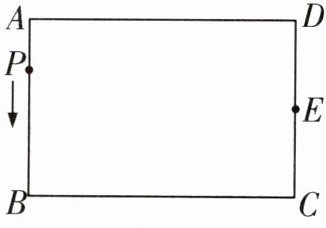
(1)当$t= 2$时,y的值是____;当$t= 6$时,y的值是____。
(2)直接写出在点P的运动过程中,y与t之间的函数关系式。

答案:
解:
(1)96 160
当 $ t = 2 $ 时,$ A P = 4 \times 2 = 8 $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } \times 24 \times 8 = 96 $;
当 $ t = 6 $ 时,$ B P = 6 \times 4 - A B = 24 - 16 = 8 $,所以 $ P C = B C - B P = 24 - 8 = 16 $,所以 $ \triangle A P E $ 的面积 $ y = 24 \times 16 - \frac { 1 } { 2 } \times 16 \times 8 - \frac { 1 } { 2 } \times ( 40 - 4 t ) \times 8 - \frac { 1 } { 2 } \times 24 \times 8 = 160 $。
(2)$ y = \left\{ \begin{array} { l } { 48 t ( 0 < t \leq 4 ) , } \\ { - 16 t + 256 ( 4 < t \leq 10 ) , } \\ { - 48 t + 576 ( 10 < t < 12 ) 。 } \end{array} \right. $
①当 $ 0 < t \leq 4 $ 时,点 $ P $ 在 $ A B $ 上(如图1),此时 $ A P = 4 t $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } \times 4 t \times 24 = 48 t $;
②当 $ 4 < t \leq 10 $ 时,点 $ P $ 在 $ B C $ 上(如图2),此时 $ B P = 4 t - 16 $,则 $ P C = 24 - ( 4 t - 16 ) = 40 - 4 t $,所以 $ \triangle A P E $ 的面积 $ y = 24 \times 16 - \frac { 1 } { 2 } \times 16 \times ( 4 t - 16 ) - \frac { 1 } { 2 } \times ( 40 - 4 t ) \times 8 - \frac { 1 } { 2 } \times 24 \times 8 = - 16 t + 256 $;
③当 $ 10 < t < 12 $ 时,点 $ P $ 在 $ C E $ 上(如图3),此时 $ P E = 48 - 4 t $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } ( 48 - 4 t ) \times 24 = - 48 t + 576 $。
综上,$ y $ 与 $ t $ 之间的函数关系式为 $ y = \left\{ \begin{array} { l } { 48 t ( 0 < t \leq 4 ) , } \\ { - 16 t + 256 ( 4 < t \leq 10 ) , } \\ { - 48 t + 576 ( 10 < t < 12 ) 。 } \end{array} \right. $



解:
(1)96 160
当 $ t = 2 $ 时,$ A P = 4 \times 2 = 8 $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } \times 24 \times 8 = 96 $;
当 $ t = 6 $ 时,$ B P = 6 \times 4 - A B = 24 - 16 = 8 $,所以 $ P C = B C - B P = 24 - 8 = 16 $,所以 $ \triangle A P E $ 的面积 $ y = 24 \times 16 - \frac { 1 } { 2 } \times 16 \times 8 - \frac { 1 } { 2 } \times ( 40 - 4 t ) \times 8 - \frac { 1 } { 2 } \times 24 \times 8 = 160 $。
(2)$ y = \left\{ \begin{array} { l } { 48 t ( 0 < t \leq 4 ) , } \\ { - 16 t + 256 ( 4 < t \leq 10 ) , } \\ { - 48 t + 576 ( 10 < t < 12 ) 。 } \end{array} \right. $
①当 $ 0 < t \leq 4 $ 时,点 $ P $ 在 $ A B $ 上(如图1),此时 $ A P = 4 t $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } \times 4 t \times 24 = 48 t $;
②当 $ 4 < t \leq 10 $ 时,点 $ P $ 在 $ B C $ 上(如图2),此时 $ B P = 4 t - 16 $,则 $ P C = 24 - ( 4 t - 16 ) = 40 - 4 t $,所以 $ \triangle A P E $ 的面积 $ y = 24 \times 16 - \frac { 1 } { 2 } \times 16 \times ( 4 t - 16 ) - \frac { 1 } { 2 } \times ( 40 - 4 t ) \times 8 - \frac { 1 } { 2 } \times 24 \times 8 = - 16 t + 256 $;
③当 $ 10 < t < 12 $ 时,点 $ P $ 在 $ C E $ 上(如图3),此时 $ P E = 48 - 4 t $,所以 $ \triangle A P E $ 的面积 $ y = \frac { 1 } { 2 } ( 48 - 4 t ) \times 24 = - 48 t + 576 $。
综上,$ y $ 与 $ t $ 之间的函数关系式为 $ y = \left\{ \begin{array} { l } { 48 t ( 0 < t \leq 4 ) , } \\ { - 16 t + 256 ( 4 < t \leq 10 ) , } \\ { - 48 t + 576 ( 10 < t < 12 ) 。 } \end{array} \right. $



查看更多完整答案,请扫码查看


