第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
7 新情境[2024郑州桐柏一中期中]勾股定理是数学定理中证明方法最多的定理之一,也是用代数思想解决几何问题最重要的工具之一。下列图形中可以证明勾股定理的有(
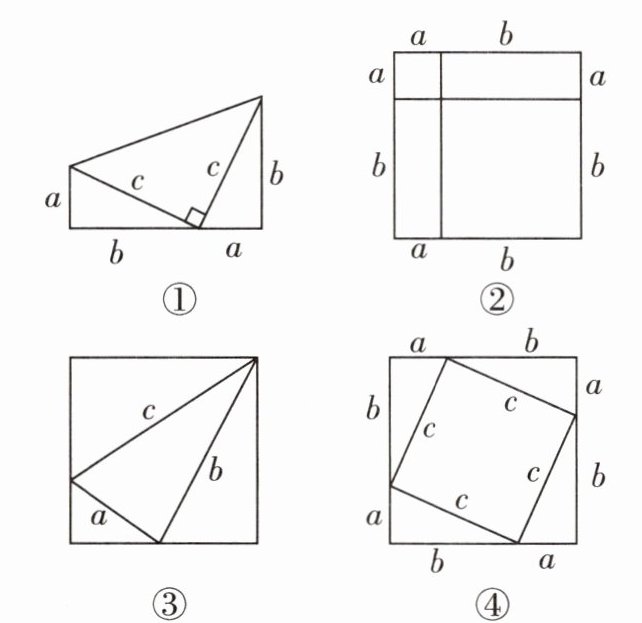
A. ①③
B. ②③
C. ②④
D. ①④
D
)
A. ①③
B. ②③
C. ②④
D. ①④
答案:
7 D 对于①,$ S_{梯形} = \frac{1}{2}(a + b)^{2} = \frac{1}{2}a^{2} + ab + \frac{1}{2}b^{2} $,$ S_{梯形} = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^{2} = ab + \frac{1}{2}c^{2} $,所以 $ \frac{1}{2}a^{2} + ab + \frac{1}{2}b^{2} = ab + \frac{1}{2}c^{2} $,整理,得 $ a^{2} + b^{2} = c^{2} $,故①符合题意;对于④,$ S_{正方形} = (a + b)^{2} = a^{2} + 2ab + b^{2} $,$ S_{正方形} = 4 \times \frac{1}{2}ab + c^{2} = 2ab + c^{2} $,所以 $ a^{2} + 2ab + b^{2} = 2ab + c^{2} $,所以 $ a^{2} + b^{2} = c^{2} $,故④符合题意;②③不符合题意。
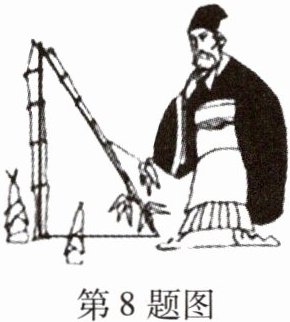
8 新趋势·数学文化[2025泉州泉港区期末]如图,《九章算术》中记载:“今有竹高一丈,末折抵地,去本三尺。问折者高几何?”译文:一根竹子,原高一丈,折断后其竹尖恰好着地,着地处离原竹子根部3尺远。问:原处还有多高的竹子?(1丈= 10尺)则竹子折断处离地面(
A. $\frac{81}{20}$尺
B. $\frac{91}{20}$尺
C. $\frac{81}{19}$尺
D. $\frac{91}{19}$尺
$\frac{91}{20}$尺
)

A. $\frac{81}{20}$尺
B. $\frac{91}{20}$尺
C. $\frac{81}{19}$尺
D. $\frac{91}{19}$尺
答案:
8 B 设竹子折断处离地面 $ x $ 尺,则折断部分为 $ (10 - x) $ 尺,根据勾股定理,得 $ x^{2} + 3^{2} = (10 - x)^{2} $,解得 $ x = \frac{91}{20} $。
归纳总结
运用勾股定理解决实际问题的一般步骤
(1) 从实际问题中抽象出几何图形;
(2) 确定要求的线段所在的直角三角形;
(3) 找准直角边和斜边,根据勾股定理建立等量关系,列出等式;
(4) 求得结果。
归纳总结
运用勾股定理解决实际问题的一般步骤
(1) 从实际问题中抽象出几何图形;
(2) 确定要求的线段所在的直角三角形;
(3) 找准直角边和斜边,根据勾股定理建立等量关系,列出等式;
(4) 求得结果。
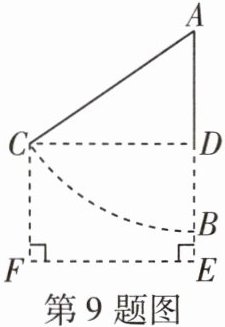
9 [2025宝鸡高新中学段考]勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一。如图,当秋千静止时,踏板B离地的垂直高度BE= 0.7m,将它往前推3m至C处时(即水平距离CD= 3m),踏板离地的垂直高度CF= 2.5m,它的绳索始终拉直,则绳索AC的长是(
A. 3.4m
B. 5m
C. 4m
D. 5.5m
3.4m
)A. 3.4m
B. 5m
C. 4m
D. 5.5m
答案:
9 A 由题意可知,$ CF = 2.5m $,$ BE = 0.7m $,所以 $ BD = 1.8m $。设 $ AC $ 的长为 $ x m $,则 $ AB = AC = x m $,所以 $ AD = AB - BD = (x - 1.8)m $。在 $ Rt \triangle ADC $ 中,$ AD^{2} + CD^{2} = AC^{2} $,即 $ (x - 1.8)^{2} + 3^{2} = x^{2} $,解得 $ x = 3.4 $,即绳索 $ AC $ 的长是 $ 3.4m $。
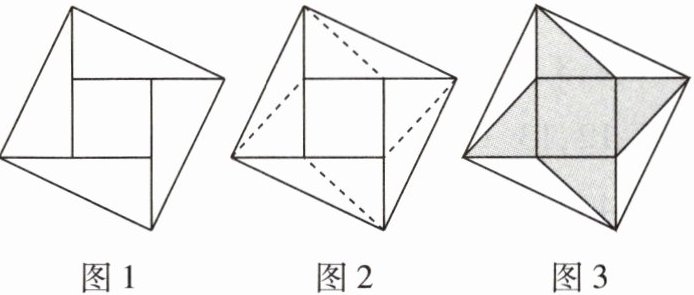
10 新趋势·数学文化[2025郑州育才中学月考]如图1,四个全等的直角三角形围成一个大正方形,中间是一个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,若图1中的直角三角形的长直角边为5,大正方形的面积为29,连接图2中四条线段得到如图3的新图案,求图3中阴影部分的面积______。

答案:
10 21 如图,根据题意,得 $ BC = 5 $,$ AC^{2} = 29 $,$ \angle ABC = 90^{\circ} $,$ AB = CD $,所以 $ AB = 2 $,所以 $ CD = 2 $,所以 $ S_{\triangle ADC} = \frac{1}{2}CD \times AB = 2 $,所以阴影部分的面积为 $ 29 - 4 \times 2 = 21 $。

10 21 如图,根据题意,得 $ BC = 5 $,$ AC^{2} = 29 $,$ \angle ABC = 90^{\circ} $,$ AB = CD $,所以 $ AB = 2 $,所以 $ CD = 2 $,所以 $ S_{\triangle ADC} = \frac{1}{2}CD \times AB = 2 $,所以阴影部分的面积为 $ 29 - 4 \times 2 = 21 $。

11 [2024沈阳辽中区期末改编]如图,一架梯子AB斜靠在某个胡同竖直的左墙上,顶端在点A处,底端在水平地面的点B处,保持梯子底端B的位置不变,将梯子斜靠在竖直的右墙上,此时梯子的顶端在点E处。已知顶端A距离地面的高度AC为2米,BC为1.5米。
(1)梯子的长为______
(2)若顶端E距离地面的高度EF比AC多0.4米,则胡同的宽CF为______
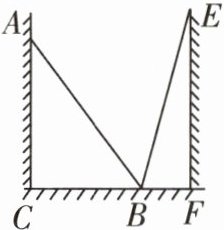
(1)梯子的长为______
2.5
米;(2)若顶端E距离地面的高度EF比AC多0.4米,则胡同的宽CF为______
2.2
米。
答案:
11
(1) 2.5;
(2) 2.2
(1) 在 $ Rt \triangle ACB $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 2 $ 米,$ BC = 1.5 $ 米,$ BC^{2} + AC^{2} = AB^{2} $,所以 $ AB^{2} = 2^{2} + 1.5^{2} = 6.25 $,所以 $ AB = 2.5 $ 米,即梯子的长为 $ 2.5 $ 米;
(2) 由题意得 $ EF = AC + 0.4 = 2.4 $ 米,$ BE = AB = 2.5 $ 米,所以 $ BF^{2} = 2.5^{2} - 2.4^{2} = 0.49 $,所以 $ BF = 0.7 $ 米,所以 $ CF = CB + BF = 1.5 + 0.7 = 2.2 $(米)。
(1) 2.5;
(2) 2.2
(1) 在 $ Rt \triangle ACB $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 2 $ 米,$ BC = 1.5 $ 米,$ BC^{2} + AC^{2} = AB^{2} $,所以 $ AB^{2} = 2^{2} + 1.5^{2} = 6.25 $,所以 $ AB = 2.5 $ 米,即梯子的长为 $ 2.5 $ 米;
(2) 由题意得 $ EF = AC + 0.4 = 2.4 $ 米,$ BE = AB = 2.5 $ 米,所以 $ BF^{2} = 2.5^{2} - 2.4^{2} = 0.49 $,所以 $ BF = 0.7 $ 米,所以 $ CF = CB + BF = 1.5 + 0.7 = 2.2 $(米)。
12 教材习题变式 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明$a^{2}+b^{2}= c^{2}$。请你写出证明过程。
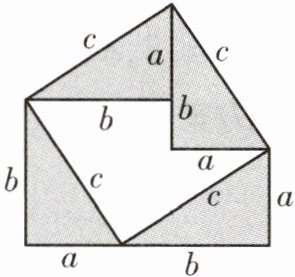

答案:
12 证明:如图,过点 $ A $ 作 $ AF \perp CD $ 于点 $ F $。因为 $ S_{五边形ABCDE} = S_{梯形ABCF} + S_{梯形AFDE} = S_{正方形ABGE} + 2S_{\triangle BCG} $,即 $ \frac{1}{2}(b + a + b) \times b + \frac{1}{2}(a + a + b) \times a = c^{2} + 2 \times \frac{1}{2}ab $,所以 $ \frac{1}{2}ab + b^{2} + a^{2} + \frac{1}{2}ab = c^{2} + ab $,所以 $ a^{2} + b^{2} = c^{2} $。

12 证明:如图,过点 $ A $ 作 $ AF \perp CD $ 于点 $ F $。因为 $ S_{五边形ABCDE} = S_{梯形ABCF} + S_{梯形AFDE} = S_{正方形ABGE} + 2S_{\triangle BCG} $,即 $ \frac{1}{2}(b + a + b) \times b + \frac{1}{2}(a + a + b) \times a = c^{2} + 2 \times \frac{1}{2}ab $,所以 $ \frac{1}{2}ab + b^{2} + a^{2} + \frac{1}{2}ab = c^{2} + ab $,所以 $ a^{2} + b^{2} = c^{2} $。

【回顾与思考】
你是如何获得勾股定理的?
你是如何获得勾股定理的?
答案:
【解析】:勾股定理的获得通常有以下几种常见方式。可以通过测量多个直角三角形的三条边的长度,然后计算各边长度的平方,经过大量数据的观察和分析,发现直角三角形两条直角边的平方和等于斜边的平方这一规律。也可以利用拼图的方法,比如用四个全等的直角三角形拼成一个大正方形,通过大正方形面积的不同表示方法来推导得出勾股定理。还可以从实际生活中的一些现象和问题出发,经过抽象和数学化的过程来总结出勾股定理。
【答案】:可以通过测量直角三角形三边长度并计算平方关系、拼图推导、从实际生活现象抽象总结等方式获得勾股定理。
【答案】:可以通过测量直角三角形三边长度并计算平方关系、拼图推导、从实际生活现象抽象总结等方式获得勾股定理。
查看更多完整答案,请扫码查看


