《2025年一遍过八年级数学上册北师大版》

7 若以B点为坐标原点,建立平面直角坐标系,则A点的坐标为(1,5)。若以A点为坐标原点,建立平面直角坐标系,则B点的坐标为 (A)
A. (-1,-5)
B. (-1,5)
C. (1,-5)
D. (1,5)

答案： A

8 [2024湛江期末]小明家位于公园的正东方向200m处,从小明家出发向正北走300m就到小华家。若选取小华家所在位置为原点,以1m为单位,分别以正东、正北方向为x轴、y轴正方向,建立平面直角坐标系,则公园的坐标是 ( )
A. (-300,-200)
B. (200,300)
C. (-200,-300)
D. (300,200)

答案：
C 根据题意,可建立如图所示的平面直角坐标系,所以公园的坐标是(-200,-300)。

9 [2024恩施州月考]如图,直线$l_1⊥l_2,$在某平面直角坐标系中,x轴$//l_1,y$轴$//l_2,$点A的坐标为(-2,-1),点B的坐标为(1,2),那么点C在第____象限。

答案：
二 因为点A的坐标为(-2,-1),点B的坐标为(1,2),所以点A位于第三象限,点B位于第一象限,根据题意可建立如图所示的平面直角坐标系,所以点C位于第二象限。

10 [2024聊城期末]如图为某中学新校区分布图的一部分,图中每个小正方形的边长都是1,若教学楼的坐标为A(1,2),图书馆的坐标为B(-2,-1),解答以下问题：
(1)在图中建立平面直角坐标系；
(2)若体育馆的坐标为C(1,-3),食堂的坐标为D(2,0),请在图中标出体育馆和食堂的位置；
(3)在(2)的条件下,顺次连接教学楼、图书馆、体育馆和食堂,得到四边形ABCD,求四边形ABCD的面积。

答案：
解:
(1)建立的平面直角坐标系如图所示。

(2)体育馆和食堂的位置如图所示。
(3)如图,四边形ABCD的面积为$4\times5-\frac{1}{2}\times3\times3-\frac{1}{2}\times2\times3-\frac{1}{2}\times1\times3-\frac{1}{2}\times1\times2=10$。

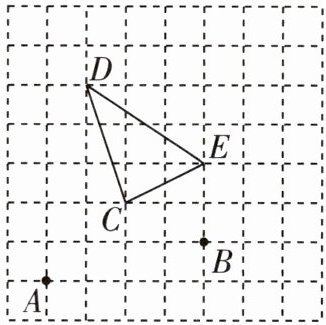
11 [2025沈阳浑南区期末]如图,用(-1,-2)表示A点位置,用(3,-1)表示B点的位置。
(1)画出平面直角坐标系,并写出点E的坐标；
(2)若点P在y轴上,且与点C在直线DE的同侧,当△PDE的面积等于△CDE的面积时,求点P的坐标。

答案：
解:
(1)画出平面直角坐标系如图所示,点E(3,1)。

(2)设点P的坐标为(0,y),且y＜3,
因为△PDE的面积等于△CDE的面积,
所以$\frac{1}{2}\times(3-y)\times3=3\times3-\frac{1}{2}\times1\times2-\frac{1}{2}\times1\times3-\frac{1}{2}\times2\times3$,解得$y=\frac{2}{3}$,
所以点P的坐标为$(0,\frac{2}{3})$。

12 几何直观 如图,在Rt△OAB中,斜边OB在x轴的正半轴上,直角顶点A在第四象限内,$S_{△OAB}= 20,$OA:AB= 1:2。求A,B两点的坐标。

答案：
解:由OA:AB=1:2,可设OA=x(x＞0),则AB=2x。
在Rt△OAB中,根据勾股定理,可得$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{5}x$。
因为$S_{\triangle OAB}=20=\frac{1}{2}OA\cdot AB$,所以$20=\frac{1}{2}x\cdot2x$,
所以$x^{2}=20$,所以$x=2\sqrt{5}$,
所以$OB=\sqrt{5}\times2\sqrt{5}=10$,所以点B的坐标是(10,0)。
如图,过点A作AC⊥OB于点C,
因为$S_{\triangle OAB}=\frac{1}{2}BO\cdot AC=20$,
所以AC=4,
又因为点A在第四象限,
所以点A的纵坐标为-4。
在Rt△AOC中,$OA=2\sqrt{5}$,AC=4,
由勾股定理,得$OC=\sqrt{OA^{2}-AC^{2}}=2$,
所以点A的横坐标是2,
所以点A的坐标为(2,-4)。

引入平面直角坐标系,对日常生活和数学学习有哪些作用？

答案： 【解析】：在日常生活中，平面直角坐标系可以帮助我们精确地描述位置。比如在地图上，通过建立类似平面直角坐标系的网格系统，我们能准确找到某个地点的具体位置，方便出行导航、地理研究等。在城市规划中，也可以利用平面直角坐标系来规划建筑物的布局等。在数学学习方面，平面直角坐标系是函数的重要载体。它能将函数关系以直观的图像形式展现出来，帮助我们更好地理解函数的性质，如单调性、奇偶性等。通过研究函数图像在坐标系中的特征，我们可以更深入地分析函数的变化规律。同时，在解析几何中，平面直角坐标系将几何问题转化为代数问题，利用坐标和方程来研究几何图形的性质和位置关系，大大简化了问题的解决过程。
【答案】：在日常生活中可精确描述位置，用于地图导航、城市规划等；在数学学习中是函数的重要载体，可直观展现函数关系、研究函数性质，还能将几何问题转化为代数问题，简化解析几何问题的解决。