《2025年一遍过八年级数学上册北师大版》

13 [2025张掖思源实验学校月考]下列计算正确的是 (B)
A.$\sqrt[3]{(-2)^{3}}= 2$
B.$\sqrt[3]{-0.064}= -0.4$
C.$(\sqrt[3]{-21})^{3}= 21$
D.$-\sqrt[3]{8\frac{1}{8}}= -2$

答案： B $\sqrt[3]{(-2)^3}=-2$, 故 A 项不符合题意; $(\sqrt[3]{-21})^3=-21$, 故 C 项不符合题意; $-\sqrt[3]{8 \frac{1}{8}}=-\sqrt[3]{\frac{65}{8}}$, 故 D 项不符合题意。

14 易错题[2025泉州诊断性考试]若$\sqrt[3]{x+3}= 2$,则$(x+3)^{2}$的平方根是$\pm 8$。

答案： $\pm 8$ 由题意可知, $x+3=8$, 所以 $(x+3)^2=64$, 所以 64的平方根是 $\pm \sqrt{64}= \pm 8$ 。

15 [2023新乡期中]已知$\sqrt[3]{x-3}-\sqrt[3]{2x+1}= 0$,则$x^{2}+x-3$的平方根为$\pm 3$。

答案： $\pm 3$ 因为 $\sqrt[3]{x-3}-\sqrt[3]{2 x+1}=0$, 所以 $x-3=2 x+1$, 所以 $x=-4$, 所以 $x^2+x-3=9$, 所以 $x^2+x-3$ 的平方根为 $\pm 3$ 。

若一个正数x的平方根是$\sqrt[3]{17-a}和\sqrt[3]{3a-1}$,则$\sqrt[3]{a}$的值为-2。

答案： 变式 -2 解题思路: 根据一个正数有两个平方根, 且它们互为相反数得到 $\sqrt[3]{17-a}+\sqrt[3]{3 a-1}=0$, 再根据立方根的定义得到 $17-a+3 a-1=0$, 从而求出 $a$ 的值, 即可求出 $\sqrt[3]{a}$的值。
因为一个正数 $x$ 的平方根是 $\sqrt[3]{17-a}$ 和 $\sqrt[3]{3 a-1}$, 所以 $\sqrt[3]{17-a}+\sqrt[3]{3 a-1}=0$, 所以 $17-a+3 a-1=0$, 所以 $a=-8$, 所以 $\sqrt[3]{a}=\sqrt[3]{-8}=-2$ 。

16 [2025绵阳游仙区模拟]已知$x^{2}= 1,\sqrt[3]{y}= -2$,且$xy＜0$,则$\sqrt{x-y}= $3。

答案： 3 因为 $x^2=1, \sqrt[3]{y}=-2$, 所以 $x= \pm 1, y=-8$, 又因为 $x y＜0$, 所以 $x=1$, 所以 $\sqrt{x-y}=\sqrt{1-(-8)}=\sqrt{9}=3$ 。

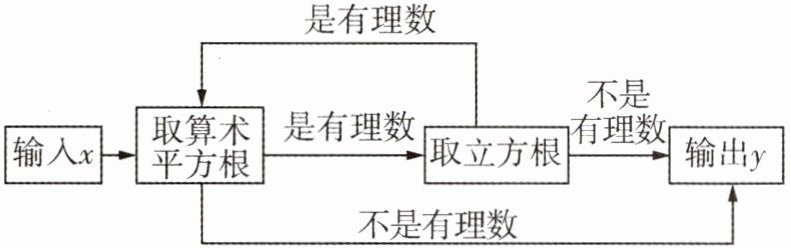
17 [2025佛山禅城区期末]小明是一位电脑爱好者,他设计了一个程序如图所示,当输入的x值为64时,输出的y值为$\sqrt{2}$。

答案： $\sqrt{2}$ 当输人的 $x$ 值为 64 时, 取算术平方根得 8,8 是有理数, 取立方根得 2,2 是有理数, 取算术平方根得 $\sqrt{2}, \sqrt{2}$ 不是有理数, 所以输出的 $y$ 值为 $\sqrt{2}$ 。

18 [2024扬州期末]已知$3m+1的平方根是\pm 5,5n-m$的立方根是3。
(1)求$m-n$的平方根。
(2)若$4a+m$的算术平方根是4,求$3a-2n$的立方根。

答案： 解:
(1)因为 $3 m+1$ 的平方根是 \pm 5,所以 $3 m+1=25$, 所以 $m=8$ 。因为 $5 n-m$ 的立方根是 3, 所以 $5 n-m=27$,又因为 $m=8$, 所以 $5 n-8=27$,所以 $n=7$, 所以 $m-n=8-7=1$,所以 $m-n$ 的平方根为 \pm 1 。
(2)由
(1)知 $m=8, n=7$,因为 $4 a+m$ 的算术平方根是 4,所以 $4 a+8=16$, 所以 $a=2$,所以 $3 a-2 n=3 \times 2-2 \times 7=-8$,所以 $3 a-2 n$ 的立方根为 -2 。

(1)求该魔方的棱长;6 cm
(2)求该长方体纸盒的表面积。440 cm²

答案： 解:
(1)设魔方的棱长为 $x \mathrm{~cm}$,根据题意, 得 $x^3=216$, 解得 $x=6$,答: 该魔方的棱长为 $6 \mathrm{~cm}$ 。
(2)设该长方体纸盒的长为 $y \mathrm{~cm}$, 则 $6 y^2=600$,所以 $y^2=100$, 解得 $y= \pm 10$,因为 $y$ 是正数, 所以 $y=10$,所以 $10 \times 10 \times 2+10 \times 6 \times 4=440\left(\mathrm{~cm}^2\right)$ 。答: 该长方体纸盒的表面积为 $440 \mathrm{~cm}^2$ 。

20 推理能力[2024北京大兴区期中]人教版教材的数学活动中有这样一段材料:我国著名数学家华罗庚有一次在飞机上看到他的助手阅读的杂志上有一道智力题:一个数是59319,求它的立方根。华罗庚脱口而出:39。华罗庚迅速求出立方根的过程如下:
假设59319的立方根是n,
①由$10^{3}= 1000,100^{3}= 1000000$,可以确定n是两位数;
②由$30^{3}= 27000,40^{3}= 64000,27000＜59319＜64000$可知,n的十位上的数是3;
③考虑到1至9的立方中,只有9的立方的个位上的数是9,所以确定n的个位上的数是9,所以$n= 39$。
请你根据上述步骤求出140608的立方根是____52。

答案： 52 假设 140608 的立方根是 $n$, 由 $10^3=1000,100^3=1000000$, 可以确定 $n$ 是两位数, 由 $50^3=125000,60^3=216000,125000＜140608＜216000$ 可知, $n$ 的十位上的数是5, 考虑 1 至 9 的立方中, 个位上的数为 8 的只有 2 的立方 8,所以确定 $n$ 的个位上的数是 2, 即 $n=52$ 。