第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
6 教材尝试·交流变式[2024大同平城区期末]商场为了满足顾客需求,将5千克奶糖、3千克酥心糖和2千克水果糖合成什锦糖出售。若奶糖的售价为40元/千克,酥心糖的售价为20元/千克,水果糖的售价为15元/千克,那么混合后什锦糖的售价为每千克(
A. 25元
B. 28.5元
C. 29元
D. 34.5元
29元
)A. 25元
B. 28.5元
C. 29元
D. 34.5元
答案:
C 根据题意,得 $ (40 \times 5 + 20 \times 3 + 15 \times 2) \div (5 + 3 + 2) = 29 $ (元),即混合后什锦糖的售价应为每千克 29 元。
7 [2025郑州管城区模拟]学校食堂有15元、18元、20元三种盒饭供学生选择(每人购一份),某天盒饭销售情况如图所示,则当天学生购买盒饭费用的平均数是(
学校食堂某天盒饭销售情况统计图
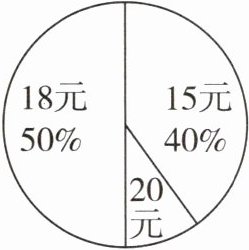
A. 16元
B. 17元
C. 18元
D. 19元
17元
)学校食堂某天盒饭销售情况统计图

A. 16元
B. 17元
C. 18元
D. 19元
答案:
B $ 18 \times 50\% + 15 \times 40\% + 20 \times (1 - 50\% - 40\%) = 9 + 6 + 2 = 17 $ (元)。
#### 归纳总结
计算统计图中数据的平均数,大多计算的是加权平均数,对应的纵轴上的数或扇形所占的百分比就是“权”。
#### 归纳总结
计算统计图中数据的平均数,大多计算的是加权平均数,对应的纵轴上的数或扇形所占的百分比就是“权”。
8 [2025沈阳期末]参加某次数学竞赛的女生和男生人数的比是1:3,这次竞赛的平均成绩是82分,其中男生的平均成绩是80分,女生的平均成绩是(
A. 82分
B. 86分
C. 87分
D. 88分
88
)A. 82分
B. 86分
C. 87分
D. 88分
答案:
D 设女生的平均成绩是 $ x $ 分,根据题意,得 $ x \times 1 + 80 \times 3 = 82 \times (1 + 3) $,解得 $ x = 88 $,即女生的平均成绩是 88 分。
9 [2024福建中考]已知A,B两地都只有甲、乙两类普通高中学校。在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分;乙类学校有考生2000人,数学平均分为80分。
(1)求A地考生的数学平均分。
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明。
(1)求A地考生的数学平均分。
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明。
答案:
解:
(1) 由题意,得 $ A $ 地考生的数学平均分为 $ \frac{1}{5000}(90 \times 3000 + 80 \times 2000) = 86 $ (分)。
(2) 不能。举例如下:
如 $ B $ 地甲类学校有考生 1000 人,乙类学校有考生 3000 人,则 $ B $ 地考生的数学平均分为 $ \frac{1}{4000}(94 \times 1000 + 82 \times 3000) = 85 $ (分),
因为 $ 85 < 86 $,所以不能判断 $ B $ 地考生数学平均分一定比 $ A $ 地考生数学平均分高。
(答案不唯一,只要能作出正确判断,并且所举的例子能说明其判断即可)
(1) 由题意,得 $ A $ 地考生的数学平均分为 $ \frac{1}{5000}(90 \times 3000 + 80 \times 2000) = 86 $ (分)。
(2) 不能。举例如下:
如 $ B $ 地甲类学校有考生 1000 人,乙类学校有考生 3000 人,则 $ B $ 地考生的数学平均分为 $ \frac{1}{4000}(94 \times 1000 + 82 \times 3000) = 85 $ (分),
因为 $ 85 < 86 $,所以不能判断 $ B $ 地考生数学平均分一定比 $ A $ 地考生数学平均分高。
(答案不唯一,只要能作出正确判断,并且所举的例子能说明其判断即可)
10 新趋势·结论开放 教材习题变式 学校坚持“德育为先、智育为重、体育为基、美育为要、劳育为本”的五育并举育人理念,拟开展校级优秀学生评比活动。下表是八年级(1)班三名同学综合素质考核的得分表:(每项满分10分,单位:分)
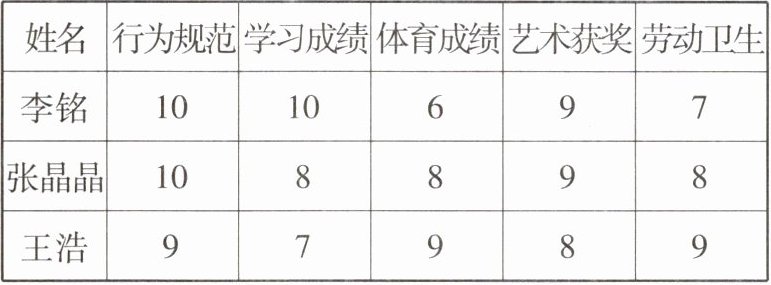
(1)如果根据五项考核的平均成绩确定推荐1人,那么被推荐的是______
(2)你认为表中五项考核成绩中最重要的是______

(1)如果根据五项考核的平均成绩确定推荐1人,那么被推荐的是______
张晶晶
。(2)你认为表中五项考核成绩中最重要的是______
学习成绩
。请你设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各项的得分重新计算,比较出大小关系,并从中推荐得分最高的作为校优秀学生的候选人。设定比例为2:4:2:1:1,李铭的成绩为8.8分,张晶晶的成绩为8.5分,王浩的成绩为8.1分,因为8.8>8.5>8.1,所以候选人为李铭。
答案:
解:
(1) 张晶晶
李铭的平均成绩为 $ \frac{1}{5} \times (10 + 10 + 6 + 9 + 7) = 8.4 $ (分),张晶晶的平均成绩为 $ \frac{1}{5} \times (10 + 8 + 8 + 9 + 8) = 8.6 $ (分),王浩的平均成绩为 $ \frac{1}{5} \times (9 + 7 + 9 + 8 + 9) = 8.4 $ (分),因为 $ 8.4 < 8.6 $,所以被推荐的是张晶晶。
(2) 学习成绩
设定比例为 $ 2:4:2:1:1 $,
李铭的成绩为 $ \frac{10 \times 2 + 10 \times 4 + 6 \times 2 + 9 + 7}{10} = 8.8 $ (分),
张晶晶的成绩为 $ \frac{10 \times 2 + 8 \times 4 + 8 \times 2 + 9 + 8}{10} = 8.5 $ (分),
王浩的成绩为 $ \frac{9 \times 2 + 7 \times 4 + 9 \times 2 + 8 + 9}{10} = 8.1 $ (分),
因为 $ 8.8 > 8.5 > 8.1 $,
所以候选人为李铭。
(答案不唯一,合理即可)
(1) 张晶晶
李铭的平均成绩为 $ \frac{1}{5} \times (10 + 10 + 6 + 9 + 7) = 8.4 $ (分),张晶晶的平均成绩为 $ \frac{1}{5} \times (10 + 8 + 8 + 9 + 8) = 8.6 $ (分),王浩的平均成绩为 $ \frac{1}{5} \times (9 + 7 + 9 + 8 + 9) = 8.4 $ (分),因为 $ 8.4 < 8.6 $,所以被推荐的是张晶晶。
(2) 学习成绩
设定比例为 $ 2:4:2:1:1 $,
李铭的成绩为 $ \frac{10 \times 2 + 10 \times 4 + 6 \times 2 + 9 + 7}{10} = 8.8 $ (分),
张晶晶的成绩为 $ \frac{10 \times 2 + 8 \times 4 + 8 \times 2 + 9 + 8}{10} = 8.5 $ (分),
王浩的成绩为 $ \frac{9 \times 2 + 7 \times 4 + 9 \times 2 + 8 + 9}{10} = 8.1 $ (分),
因为 $ 8.8 > 8.5 > 8.1 $,
所以候选人为李铭。
(答案不唯一,合理即可)
加权平均数和算术平均数有什么区别和联系?
一遍过 初中数学 八年级上册 55
一遍过 初中数学 八年级上册 55
答案:
【解析】:
### 区别
1. **定义不同**
算术平均数是一组数据中所有数据之和再除以这组数据的个数。若有$n$个数$x_1,x_2,\cdots,x_n$,则它们的算术平均数$\overline{x}=\frac{x_1 + x_2+\cdots+x_n}{n}$。例如,数据$2$、$4$、$6$的算术平均数为$\frac{2 + 4+6}{3}=4$。
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算。若$n$个数$x_1,x_2,\cdots,x_n$的权数分别是$\omega_1,\omega_2,\cdots,\omega_n$,那么$\overline{x}=\frac{x_1\omega_1 + x_2\omega_2+\cdots+x_n\omega_n}{\omega_1+\omega_2+\cdots+\omega_n}$。比如,学生的数学考试成绩,平时作业占$20\%$,期中考试占$30\%$,期末考试占$50\%$。某学生平时作业成绩为$80$分,期中考试成绩为$85$分,期末考试成绩为$90$分,那么该学生的数学总评成绩就是加权平均数,即$\overline{x}=\frac{80\times0.2 + 85\times0.3+90\times0.5}{0.2 + 0.3+0.5}=86.5$分。
2. **意义不同**
算术平均数反映了一组数据的平均大小,常用来代表数据的总体“平均水平”,每个数据在计算中所占的地位是平等的。
加权平均数反映的是在考虑各数据重要程度不同的情况下的平均水平,数据的权能够反映数据的相对“重要程度”。
### 联系
1. 加权平均数是算术平均数的一种特殊情况。当各数据的权数都相等时,加权平均数就等于算术平均数。例如,若$n$个数$x_1,x_2,\cdots,x_n$的权数$\omega_1=\omega_2=\cdots=\omega_n = 1$,此时加权平均数$\overline{x}=\frac{x_1\times1 + x_2\times1+\cdots+x_n\times1}{1 + 1+\cdots+1}=\frac{x_1 + x_2+\cdots+x_n}{n}$,这就是算术平均数的计算公式。
2. 二者都用于描述一组数据的集中趋势,都是平均数的表现形式,在一定程度上都可以作为数据的代表值来反映数据的总体特征。
【答案】:区别:1. 定义上,算术平均数是所有数据之和除以数据个数;加权平均数是不同比重数据按合理比例计算的平均数。2. 意义上,算术平均数代表总体“平均水平”,各数据地位平等;加权平均数考虑数据重要程度不同,权数反映数据相对“重要程度”。联系:1. 加权平均数是算术平均数的特殊情况,当各数据权数相等时,加权平均数等于算术平均数。2. 二者都用于描述数据集中趋势,都是平均数表现形式,可作为数据代表值反映总体特征。
### 区别
1. **定义不同**
算术平均数是一组数据中所有数据之和再除以这组数据的个数。若有$n$个数$x_1,x_2,\cdots,x_n$,则它们的算术平均数$\overline{x}=\frac{x_1 + x_2+\cdots+x_n}{n}$。例如,数据$2$、$4$、$6$的算术平均数为$\frac{2 + 4+6}{3}=4$。
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算。若$n$个数$x_1,x_2,\cdots,x_n$的权数分别是$\omega_1,\omega_2,\cdots,\omega_n$,那么$\overline{x}=\frac{x_1\omega_1 + x_2\omega_2+\cdots+x_n\omega_n}{\omega_1+\omega_2+\cdots+\omega_n}$。比如,学生的数学考试成绩,平时作业占$20\%$,期中考试占$30\%$,期末考试占$50\%$。某学生平时作业成绩为$80$分,期中考试成绩为$85$分,期末考试成绩为$90$分,那么该学生的数学总评成绩就是加权平均数,即$\overline{x}=\frac{80\times0.2 + 85\times0.3+90\times0.5}{0.2 + 0.3+0.5}=86.5$分。
2. **意义不同**
算术平均数反映了一组数据的平均大小,常用来代表数据的总体“平均水平”,每个数据在计算中所占的地位是平等的。
加权平均数反映的是在考虑各数据重要程度不同的情况下的平均水平,数据的权能够反映数据的相对“重要程度”。
### 联系
1. 加权平均数是算术平均数的一种特殊情况。当各数据的权数都相等时,加权平均数就等于算术平均数。例如,若$n$个数$x_1,x_2,\cdots,x_n$的权数$\omega_1=\omega_2=\cdots=\omega_n = 1$,此时加权平均数$\overline{x}=\frac{x_1\times1 + x_2\times1+\cdots+x_n\times1}{1 + 1+\cdots+1}=\frac{x_1 + x_2+\cdots+x_n}{n}$,这就是算术平均数的计算公式。
2. 二者都用于描述一组数据的集中趋势,都是平均数的表现形式,在一定程度上都可以作为数据的代表值来反映数据的总体特征。
【答案】:区别:1. 定义上,算术平均数是所有数据之和除以数据个数;加权平均数是不同比重数据按合理比例计算的平均数。2. 意义上,算术平均数代表总体“平均水平”,各数据地位平等;加权平均数考虑数据重要程度不同,权数反映数据相对“重要程度”。联系:1. 加权平均数是算术平均数的特殊情况,当各数据权数相等时,加权平均数等于算术平均数。2. 二者都用于描述数据集中趋势,都是平均数表现形式,可作为数据代表值反映总体特征。
查看更多完整答案,请扫码查看


