第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 在某校举办的学习强国演讲比赛中,六位评委给小华的评分(单位:分)分别为8,7.5,9.5,8.5,8.5,9,则小华此次演讲比赛得分的离差平方和为
2.5
。
答案:
2.5 小华此次演讲比赛得分的平均数为$\frac {1}{6}×(8 + 7.5 + 9.5 + 8.5 + 8.5 + 9) = 8.5$(分),则小华此次演讲比赛得分的离差平方和为$(8 - 8.5)^{2} + (7.5 - 8.5)^{2} + (9.5 - 8.5)^{2} + (8.5 - 8.5)^{2} + (8.5 - 8.5)^{2} + (9 - 8.5)^{2} = 2.5$。
2 [2024黑龙江龙东地区中考]一组数据2,3,3,4,则这组数据的方差为 (
A. 1
B. 0.8
C. 0.6
D. 0.5
D
)A. 1
B. 0.8
C. 0.6
D. 0.5
答案:
D 这组数据的平均数是$\frac {1}{4}×(2 + 3 + 3 + 4) = 3$,则这组数据的方差为$\frac {1}{4}×[(2 - 3)^{2} + 2×(3 - 3)^{2} + (4 - 3)^{2}] = 0.5$。
3 教材素材变式[2024烟台中考]射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为$s_{甲}^{2}和s_{乙}^{2}$,则$s_{甲}^{2}和s_{乙}^{2}$的大小关系是 (
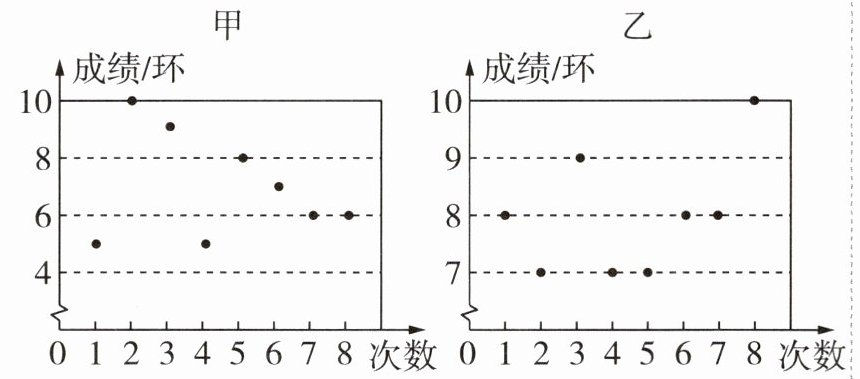
A. $s_{甲}^{2}>s_{乙}^{2}$
B. $s_{甲}^{2}<s_{乙}^{2}$
C. $s_{甲}^{2}= s_{乙}^{2}$
D. 无法确定
$s^{2}_{甲} > s^{2}_{乙}$
)
A. $s_{甲}^{2}>s_{乙}^{2}$
B. $s_{甲}^{2}<s_{乙}^{2}$
C. $s_{甲}^{2}= s_{乙}^{2}$
D. 无法确定
答案:
A 由题图可知,甲选手的数据浮动较大,所以甲选手的成绩波动较大,所以甲选手成绩的方差较大,即$s^{2}_{甲} > s^{2}_{乙}$。
为了比较甲、乙、丙三种水稻秧苗的长势,每种秧苗各随机抽取40株,分别量出每株高度,计算发现三组秧苗的平均高度一样,并且得到甲、乙、丙三组秧苗高度的方差分别是3.6,10.8,15.8,由此可知
甲
种秧苗长势更整齐。(填“甲”“乙”或“丙”)
答案:
甲 因为甲、乙、丙三组秧苗高度的方差分别是 3.6,10.8,15.8,所以甲组秧苗高度的方差最小,所以甲种秧苗长势更整齐。
归纳总结
(1)方差、标准差是描述一组数据离散程度的量,方差、标准差越小,这组数据的离散程度越小,这组数据越稳定;方差、标准差越大,这组数据的离散程度越大,这组数据波动越大。
(2)方差的单位是原数据单位的平方(一般不加单位),标准差的单位与原数据单位保持一致。
归纳总结
(1)方差、标准差是描述一组数据离散程度的量,方差、标准差越小,这组数据的离散程度越小,这组数据越稳定;方差、标准差越大,这组数据的离散程度越大,这组数据波动越大。
(2)方差的单位是原数据单位的平方(一般不加单位),标准差的单位与原数据单位保持一致。
5 一题多解已知一组数据为97,98,99,100,101,则这组数据的标准差是
$\sqrt{2}$
。
答案:
$\sqrt {2}$ 通解 $\overline {x} = \frac {1}{5}×(97 + 98 + 99 + 100 + 101) = 99,s^{2} = \frac {1}{5}×[(97 - 99)^{2} + (98 - 99)^{2} + (99 - 99)^{2} + (100 - 99)^{2} + (101 - 99)^{2}] = 2$,所以这组数据的标准差是$\sqrt {2}$。
另解 将数据 97,98,99,100,101 都减去 100 后,得到一组新数据 -3,-2,-1,0,1,新数据的平均数$\overline {x} = \frac {1}{5}×(-3 - 2 - 1 + 0 + 1) = -1,s^{2} = \frac {1}{5}×{[(-3) - (-1)]^{2} + [(-2) - (-1)]^{2} + [(-1) - (-1)]^{2} + [0 - (-1)]^{2} + [1 - (-1)]^{2}} = 2$,所以数据 97,98,99,100,101 的标准差是$\sqrt {2}$。
另解 将数据 97,98,99,100,101 都减去 100 后,得到一组新数据 -3,-2,-1,0,1,新数据的平均数$\overline {x} = \frac {1}{5}×(-3 - 2 - 1 + 0 + 1) = -1,s^{2} = \frac {1}{5}×{[(-3) - (-1)]^{2} + [(-2) - (-1)]^{2} + [(-1) - (-1)]^{2} + [0 - (-1)]^{2} + [1 - (-1)]^{2}} = 2$,所以数据 97,98,99,100,101 的标准差是$\sqrt {2}$。
6 [2025聊城月考]已知一个样本-1,0,2,x,3,平均数为2,则这个样本的方差是
6
,标准差是$\sqrt {6}$
。
答案:
6 $\sqrt {6}$ 由题意,得$\frac {1}{5}×(-1 + 0 + 2 + x + 3) = 2$,所以$-1 + 0 + 2 + x + 3 = 10$,解得$x = 6$,所以方差为$\frac {1}{5}×[(-1 - 2)^{2} + (0 - 2)^{2} + (2 - 2)^{2} + (6 - 2)^{2} + (3 - 2)^{2}] = 6$,所以标准差是$\sqrt {6}$。
7 [2025宁德月考]在我校射箭队的一次训练中,甲、乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表。

甲的射击成绩折线图
乙运动员成绩统计表(单位:环)

(1)甲运动员前5箭射击成绩的众数是
(2)求乙运动员第5次的成绩。
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由。

甲的射击成绩折线图
乙运动员成绩统计表(单位:环)

(1)甲运动员前5箭射击成绩的众数是
9
环。(2)求乙运动员第5次的成绩。
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由。
答案:
解:
(1)9
(2)因为甲运动员前5箭的总成绩是$5 + 7 + 9 + 9 + 10 = 40$(环),甲、乙两名运动员前5箭的平均成绩相同,所以$a = 40 - 8 - 10 - 8 - 6 = 8$。故乙运动员第5次的成绩是8环。
(3)因为$40×\frac {1}{5} = 8$(环),所以甲运动员前5箭射击成绩的方差$s^{2}_{甲} = \frac {1}{5}[(9 - 8)^{2} + (5 - 8)^{2} + (10 - 8)^{2} + (7 - 8)^{2} + (9 - 8)^{2}] = 3.2$,乙运动员前5箭射击成绩的方差$s^{2}_{乙} = \frac {1}{5}[(8 - 8)^{2} + (10 - 8)^{2} + (8 - 8)^{2} + (6 - 8)^{2} + (8 - 8)^{2}] = 1.6$,因为甲、乙两名运动员前5箭的平均成绩相同,$s^{2}_{甲} = 3.2 > s^{2}_{乙} = 1.6$,所以乙运动员前5箭的成绩比较稳定,应选乙运动员参加全市中学生比赛。
(1)9
(2)因为甲运动员前5箭的总成绩是$5 + 7 + 9 + 9 + 10 = 40$(环),甲、乙两名运动员前5箭的平均成绩相同,所以$a = 40 - 8 - 10 - 8 - 6 = 8$。故乙运动员第5次的成绩是8环。
(3)因为$40×\frac {1}{5} = 8$(环),所以甲运动员前5箭射击成绩的方差$s^{2}_{甲} = \frac {1}{5}[(9 - 8)^{2} + (5 - 8)^{2} + (10 - 8)^{2} + (7 - 8)^{2} + (9 - 8)^{2}] = 3.2$,乙运动员前5箭射击成绩的方差$s^{2}_{乙} = \frac {1}{5}[(8 - 8)^{2} + (10 - 8)^{2} + (8 - 8)^{2} + (6 - 8)^{2} + (8 - 8)^{2}] = 1.6$,因为甲、乙两名运动员前5箭的平均成绩相同,$s^{2}_{甲} = 3.2 > s^{2}_{乙} = 1.6$,所以乙运动员前5箭的成绩比较稳定,应选乙运动员参加全市中学生比赛。
查看更多完整答案,请扫码查看


