第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 [2024烟台中考]下列实数中的无理数是(
A. $\frac{2}{3}$
B. 3.14
C. $\sqrt{15}$
D. $\sqrt[3]{64}$
C
)A. $\frac{2}{3}$
B. 3.14
C. $\sqrt{15}$
D. $\sqrt[3]{64}$
答案:
C $\frac{2}{3}$ 是分数,3.14 是有限小数,$\sqrt[3]{64} = 4$ 是整数,它们不是无理数。$\sqrt{15}$ 是无限不循环小数,它是无理数。
2 [2024南充中考]如图,数轴上表示$\sqrt{2}$的点是(
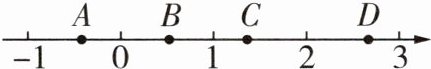
A. 点A
B. 点B
C. 点C
D. 点D
C
)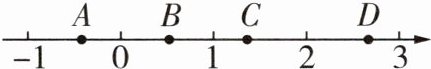
A. 点A
B. 点B
C. 点C
D. 点D
答案:
C
3 [2024自贡中考]在$0$,$-2$,$-\sqrt{3}$,$\pi$四个数中,最大的数是(
A. $-2$
B. 0
C. $\pi$
D. $-\sqrt{3}$
C
)A. $-2$
B. 0
C. $\pi$
D. $-\sqrt{3}$
答案:
C
4 [2024济宁中考]下列运算正确的是(
A. $\sqrt{2} + \sqrt{3} = \sqrt{5}$
B. $\sqrt{2}×\sqrt{5} = \sqrt{10}$
C. $2÷\sqrt{2} = 1$
D. $\sqrt{(-5)^{2}} = -5$
B
)A. $\sqrt{2} + \sqrt{3} = \sqrt{5}$
B. $\sqrt{2}×\sqrt{5} = \sqrt{10}$
C. $2÷\sqrt{2} = 1$
D. $\sqrt{(-5)^{2}} = -5$
答案:
B $\sqrt{2}$ 和 $\sqrt{3}$ 不能合并,$2 \div \sqrt{2} = \sqrt{2}$,$\sqrt{(-5)^2} = 5$。
计算$\sqrt{9^{2} - 6^{2}}$所得结果是(
A. 3
B. $\sqrt{6}$
C. $3\sqrt{5}$
D. $\pm 3\sqrt{5}$
$3\sqrt{5}$
)A. 3
B. $\sqrt{6}$
C. $3\sqrt{5}$
D. $\pm 3\sqrt{5}$
答案:
通解 $\sqrt{9^2 - 6^2} = \sqrt{81 - 36} = \sqrt{45} = 3\sqrt{5}$。
另解 $\sqrt{9^2 - 6^2} = \sqrt{(9 + 6)(9 - 6)} = \sqrt{15 \times 3} = 3\sqrt{5}$。
另解 $\sqrt{9^2 - 6^2} = \sqrt{(9 + 6)(9 - 6)} = \sqrt{15 \times 3} = 3\sqrt{5}$。
6 [2024重庆中考A卷]已知$m = \sqrt{27} - \sqrt{3}$,则实数$m$的范围是(
A. $2 < m < 3$
B. $3 < m < 4$
C. $4 < m < 5$
D. $5 < m < 6$
B
)A. $2 < m < 3$
B. $3 < m < 4$
C. $4 < m < 5$
D. $5 < m < 6$
答案:
B $m = \sqrt{27} - \sqrt{3} = 3\sqrt{3} - \sqrt{3} = 2\sqrt{3} = \sqrt{12}$,因为 $\sqrt{9} < \sqrt{12} < \sqrt{16}$,所以 $3 < \sqrt{12} < 4$,即实数 $m$ 的范围是 $3 < m < 4$。
7 [2024乐山中考]已知$1 < x < 2$,化简$\sqrt{(x - 1)^{2}} + |x - 2|$的结果为(
A. $-1$
B. 1
C. $2x - 3$
D. $3 - 2x$
B
)A. $-1$
B. 1
C. $2x - 3$
D. $3 - 2x$
答案:
B 因为 $1 < x < 2$,所以 $x - 1 > 0$,$x - 2 < 0$,所以 $\sqrt{(x - 1)^2} + |x - 2| = x - 1 + 2 - x = 1$。
8 [2024德阳中考]将一组数$\sqrt{2}$,$2$,$\sqrt{6}$,$2\sqrt{2}$,$\sqrt{10}$,$2\sqrt{3}$,…,$\sqrt{2n}$,…,按以下方式进行排列:
第一行 $\sqrt{2}$
第二行 $2$ $\sqrt{6}$
第三行 $2\sqrt{2}$ $\sqrt{10}$ $2\sqrt{3}$
……
则第八行左起第1个数是(
A. $7\sqrt{2}$
B. $8\sqrt{2}$
C. $\sqrt{58}$
D. $4\sqrt{7}$
第一行 $\sqrt{2}$
第二行 $2$ $\sqrt{6}$
第三行 $2\sqrt{2}$ $\sqrt{10}$ $2\sqrt{3}$
……
则第八行左起第1个数是(
$\sqrt{58}$
)A. $7\sqrt{2}$
B. $8\sqrt{2}$
C. $\sqrt{58}$
D. $4\sqrt{7}$
答案:
C 由题意可得前七行所有的数的总个数为 $1 + 2 + 3 + 4 + 5 + 6 + 7 = 28$,则第八行左起第 1 个数是第 29 个数,即 $\sqrt{29 \times 2} = \sqrt{58}$。
9 [新趋势·结论开放][2023青海中考]写出一个比$-\sqrt{2}大且比\sqrt{2}$小的整数:
-1(或 0 或 1)
。
答案:
-1(或 0 或 1) 因为 $1 < 2 < 4$,所以 $1 < \sqrt{2} < 2$,所以 $-2 < -\sqrt{2} < -1$,所以比 $-\sqrt{2}$ 大且比 $\sqrt{2}$ 小的整数有 -1,0,1。
10 [2024南京中考]计算$\frac{\sqrt{6}×\sqrt{8}}{\sqrt{2}}$的结果是
$2\sqrt{6}$
。
答案:
$2\sqrt{6}$ $\frac{\sqrt{6} \times \sqrt{8}}{\sqrt{2}} = \frac{\sqrt{48}}{\sqrt{2}} = \sqrt{\frac{48}{2}} = \sqrt{24} = 2\sqrt{6}$。
11 [2023宁夏中考]如图,点$A$,$B$,$C$在数轴上,点$A表示的数是-1$,点$B是AC$的中点,线段$AB = \sqrt{2}$,则点$C$表示的数是

$2\sqrt{2} - 1$
。
答案:
$2\sqrt{2} - 1$ 因为点 $A$ 表示的数是 -1,线段 $AB = \sqrt{2}$,所以点 $B$ 表示的数是 $-1 + \sqrt{2}$,因为点 $B$ 是 $AC$ 的中点,所以线段 $BC = AB = \sqrt{2}$,所以点 $C$ 表示的数是 $-1 + \sqrt{2} + \sqrt{2} = 2\sqrt{2} - 1$。
12 [新趋势·结论开放][2024深圳中考]如图,四边形$ABCD$,$DEFG$,$GHIJ$均为正方形,若$S_{正方形ABCD} = 10$,$S_{正方形GHIJ} = 1$,则正方形$DEFG$的边长可以是____
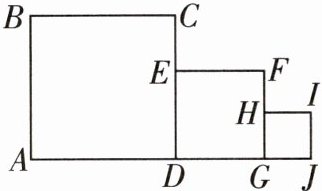
2
。(写出一个答案即可)
答案:
(答案不唯一)2 因为 $S_{正方形ABCD} = 10$,$S_{正方形GHU} = 1$,所以 $CD = \sqrt{10}$,$GH = 1$,所以 $1 < DE < \sqrt{10}$,所以正方形 $DEFG$ 的边长可以是 2。
13 [2023金昌中考]计算:$\sqrt{27}÷\frac{\sqrt{3}}{2}×2\sqrt{2} - 6\sqrt{2}$。
答案:
解:$\sqrt{27} \div \frac{\sqrt{3}}{2} \times 2\sqrt{2} - 6\sqrt{2}$
$= 3\sqrt{3} \times \frac{2}{\sqrt{3}} \times 2\sqrt{2} - 6\sqrt{2}$
$= 12\sqrt{2} - 6\sqrt{2}$
$= 6\sqrt{2}$。
$= 3\sqrt{3} \times \frac{2}{\sqrt{3}} \times 2\sqrt{2} - 6\sqrt{2}$
$= 12\sqrt{2} - 6\sqrt{2}$
$= 6\sqrt{2}$。
14 [2023上海中考]计算:$\sqrt[3]{8} + \frac{1}{2 + \sqrt{5}} - (\frac{1}{3})^{-2} + |\sqrt{5} - 3|$。
答案:
解:$\sqrt[3]{8} + \frac{1}{2 + \sqrt{5}} - (\frac{1}{3})^{-2} + |\sqrt{5} - 3|$
$= 2 + \frac{\sqrt{5} - 2}{(\sqrt{5} + 2)(\sqrt{5} - 2)} - 9 + 3 - \sqrt{5}$
$= 2 + \sqrt{5} - 2 - 9 + 3 - \sqrt{5}$
$= -6$。
$= 2 + \frac{\sqrt{5} - 2}{(\sqrt{5} + 2)(\sqrt{5} - 2)} - 9 + 3 - \sqrt{5}$
$= 2 + \sqrt{5} - 2 - 9 + 3 - \sqrt{5}$
$= -6$。
查看更多完整答案,请扫码查看


