《2025年一遍过八年级数学上册北师大版》

1 [2024南充中考]学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制)。选手李林控球技能得90分,投球技能得80分。李林综合成绩为(86分)
A. 170分
B. 86分
C. 85分
D. 84分

答案： B 李林综合成绩为 $ 90 \times 60\% + 80 \times 40\% = 86 $ (分)。
#### 归纳总结
算术平均数与加权平均数的联系与区别
(1) 当各数据的权均为 1 时，加权平均数就是算术平均数。
(2) 算术平均数是加权平均数的一种特殊形式。
(3) 加权平均数的权一般不相等，所以加权平均数不一定是算术平均数。
(4) 数据权的差异会影响平均数的大小。

2 教材例题变式[2025长春质检]小彩参加“吾有所爱,其名华夏”主题演讲比赛,形象、表达、内容三项得分分别是9分、8分、10分(每项满分为10分)。若将三项得分依次按1:5:4的比例确定最终成绩,则小彩的最终比赛成绩为(8.9分)
A. 9.3分
B. 8.9分
C. 9分
D. 9.6分

答案： B 因为形象、表达、内容三项得分依次按 $ 1:5:4 $ 的比例确定最终成绩，所以最终成绩为 $ \frac{9 \times 1 + 8 \times 5 + 10 \times 4}{1 + 5 + 4} = 8.9 $ (分)。
#### 归纳总结
(1) “权”代表的是数据的“重要程度”。一组数据中，“权”越大，数据就越“重要”。
(2) 权的三种表现形式：①各个数据出现的次数；②比例的形式；③百分比的形式。
(3) 当一组数据中有不同程度的重复数据时，一般采用加权平均数的公式来计算平均数，比较方便。

3 [2025兰州安宁区期末]在植树节当天,某班同学分成10个小组参加植树造林活动,10个小组植树的株数如表：

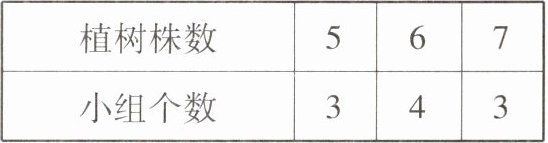
则这10个小组植树株数的平均数是(6)
A. 6
B. 6.2
C. 7
D. 6.5

答案： A 这 10 个小组植树株数的平均数是 $ \frac{5 \times 3 + 6 \times 4 + 7 \times 3}{10} = 6 $。

4 新考法[2024深圳光明区期末]某学校考察各个班级的教室卫生情况时包括以下四项：黑板、门窗、桌椅、地面。其中“地面”最重要,“桌椅和黑板”次之,对“门窗”要求最低。根据这个要求,对黑板、门窗、桌椅、地面四项考察比较合适的比例设计分别为(B)
A. 10%,15%,35%,40%
B. 15%,10%,35%,40%
C. 15%,10%,40%,35%
D. 10%,35%,15%,40%

答案： B

5 [2024江门新会区月考]某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分。前5名候选人的得分如表：

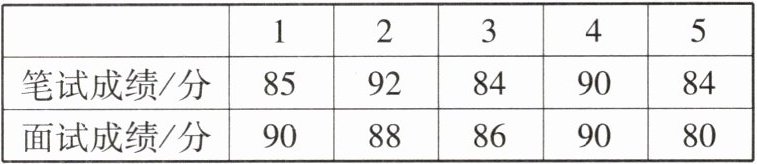
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)。
(1)现得知1号候选人的综合成绩为88分,求笔试成绩和面试成绩分别占的百分比。
(2)在(1)的条件下,求出其余4名候选人的综合成绩,并以综合成绩排序确定前2名人选。
(1)笔试成绩和面试成绩占的百分比分别是40%，60%。
(2)2号候选人的综合成绩是89.6分，3号候选人的综合成绩是85.2分，4号候选人的综合成绩是90分，5号候选人的综合成绩是81.6分，综合成绩排序前2名的人选是4号和2号。

答案： 解：
(1) 设笔试成绩占的百分比是 $ x $，则面试成绩占的百分比是 $ 1 - x $，
根据题意，得 $ 85x + 90(1 - x) = 88 $，
解得 $ x = 0.4 $，所以 $ 1 - x = 0.6 $，
所以笔试成绩和面试成绩占的百分比分别是 $ 40\% $，$ 60\% $。
(2) 2 号候选人的综合成绩是 $ 92 \times 0.4 + 88 \times 0.6 = 89.6 $ (分)，
3 号候选人的综合成绩是 $ 84 \times 0.4 + 86 \times 0.6 = 85.2 $ (分)，
4 号候选人的综合成绩是 $ 90 \times 0.4 + 90 \times 0.6 = 90 $ (分)，
5 号候选人的综合成绩是 $ 84 \times 0.4 + 80 \times 0.6 = 81.6 $ (分)，
因为 $ 90 ＞ 89.6 ＞ 88 ＞ 85.2 ＞ 81.6 $，所以综合成绩排序前 2 名的人选是 4 号和 2 号。