第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
11 [2024南通崇川区月考]如果$y= (m-2)x+m^{2}-4$是y关于x的正比例函数,点$A(m,a)和点B(-m,b)$在该函数的图象上,那么a和b的大小关系是 (
A.$a\lt b$
B.$a>b$
C.$a≤b$
D.$a≥b$
B
)A.$a\lt b$
B.$a>b$
C.$a≤b$
D.$a≥b$
答案:
B 因为$y=(m-2)x+m^{2}-4$是$y$关于$x$的正比例函数,所以$m-2≠0$且$m^{2}-4=0$,所以$m=-2$,所以正比例函数的表达式为$y=-4x$。因为$k=-4<0$,所以$y$随$x$的增大而减小,又因为点$A(m,a)$和点$B(-m,b)$在该函数的图象上,且$m<-m$,所以$a>b$。
12 跨学科·物理 一题多解[2025西安秦汉中学模拟]如图表示光从空气进入水中前与进入水中后的光路图,若建立如图所示的平面直角坐标系,并设入水前与入水后光线所在直线的表达式分别为$y_{1}= k_{1}x,y_{2}= k_{2}x$,则关于$k_{1}与k_{2}$的关系,正确的是 (
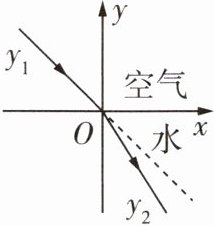
A.$k_{1}>0,k_{2}<0$
B.$k_{1}>0,k_{2}>0$
C.$|k_{1}|<|k_{2}|$
D.$|k_{1}|>|k_{2}|$
C
)
A.$k_{1}>0,k_{2}<0$
B.$k_{1}>0,k_{2}>0$
C.$|k_{1}|<|k_{2}|$
D.$|k_{1}|>|k_{2}|$
答案:
C 通解 在两个图象上分别取横坐标为1的两个点$A$和$B$,则$A(1,k_{1})$,$B(1,k_{2})$,结合题中图象可得$k_{1}>k_{2}$,因为$k_{1}<0$,$k_{2}<0$,所以$|k_{1}|<|k_{2}|$。
优解 由题中图象可知,$k_{1}<0$,$k_{2}<0$,根据直线越陡,$|k|$越大,可得$|k_{1}|<|k_{2}|$。
优解 由题中图象可知,$k_{1}<0$,$k_{2}<0$,根据直线越陡,$|k|$越大,可得$|k_{1}|<|k_{2}|$。
13 定义运算:$a*b= \left\{\begin{array}{l} ab(b>0),\\ -ab(b≤0)\end{array}\right. $如:$1*(-2)= -1×(-2)= 2$。则函数$y= 2*x$的图象大致是 (

C
)
答案:
C 根据定义运算,得$y=2*x=\left\{\begin{array}{l} 2x(x>0),\\ -2x(x≤0),\end{array}\right. $当$x>0$时,$y=2*x$的图象是直线$y=2x$在$y$轴右侧的部分;当$x≤0$时,$y=2*x$的图象是直线$y=-2x$在$y$轴左侧的部分且包含原点。
14 [2025合肥五十中期中]已知正比例函数$y= kx$,当$-4≤x≤4$时,函数有最大值3,则k的值为
$\frac{3}{4}$或$-\frac{3}{4}$
。
答案:
$\frac{3}{4}$或$-\frac{3}{4}$ 当$k>0$时,函数$y$随$x$的增大而增大,所以当$x=4$时,$y=3$,所以$4k=3$,解得$k=\frac{3}{4}$;当$k<0$时,函数$y$随$x$的增大而减小,所以当$x=-4$时,$y=3$,所以$-4k=3$,解得$k=-\frac{3}{4}$,所以$k$的值为$\frac{3}{4}$或$-\frac{3}{4}$。
15 一题多解如图,过点$A(2,0)$作x轴的垂线,与正比例函数$y= x和y= 3x$的图象分别相交于点B,C,则$\triangle OCB$的面积为
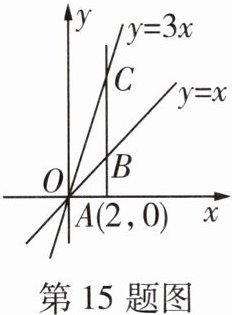
4
。
答案:
4 通解 把$x=2$分别代入$y=x$和$y=3x$,可得点$B$的坐标是$(2,2)$,点$C$的坐标是$(2,6)$,所以$BC=6-2=4$。因为点$A$的坐标是$(2,0)$,所以$OA=2$,所以$S_{\triangle OCB}=\frac{1}{2}BC\cdot OA=\frac{1}{2}×4×2=4$。
另解 同解法一,求出$B(2,2)$,$C(2,6)$,则$S_{\triangle OCB}=S_{\triangle OAC}-S_{\triangle OAB}=\frac{1}{2}×2×6-\frac{1}{2}×2×2=4$。
另解 同解法一,求出$B(2,2)$,$C(2,6)$,则$S_{\triangle OCB}=S_{\triangle OAC}-S_{\triangle OAB}=\frac{1}{2}×2×6-\frac{1}{2}×2×2=4$。
16 [2024济南期中]如图,在平面直角坐标系中,函数$y_{1}= 2x和y_{2}= -x的图象分别为直线l_{1},l_{2}$,过点$(1,0)$作x轴的垂线交$l_{1}于点A_{1}$,过点$A_{1}$作y轴的垂线交$l_{2}于点A_{2}$,过点$A_{2}$作x轴的垂线交$l_{1}于点A_{3}$,过点$A_{3}$作y轴的垂线交$l_{2}于点A_{4}$……依次进行下去,则点$A_{9}$的坐标为
$(16,32)$
,点$A_{2025}$的坐标为$(2^{1012},2^{1013})$
。
答案:
$(16,32)$ $(2^{1012},2^{1013})$ 当$x=1$时,$y_{1}=2$,所以点$A_{1}$的坐标为$(1,2)$;当$y_{2}=2$时,$x=-2$,所以点$A_{2}$的坐标为$(-2,2)$。同理可得,$A_{3}(-2,-4)$,$A_{4}(4,-4)$,$A_{5}(4,8)$,$A_{6}(-8,8)$,$A_{7}(-8,-16)$,$A_{8}(16,-16)$,$A_{9}(16,32)$,…,所以$A_{4n+1}(2^{2n},2^{2n+1})$,$A_{4n+2}(-2^{2n+1},2^{2n+1})$,$A_{4n+3}(-2^{2n+1},-2^{2n+2})$,$A_{4n+4}(2^{2n+2},-2^{2n+2})$,其中$n$为自然数。因为$2025=506×4+1$,所以点$A_{2025}$的坐标为$(2^{506×2},2^{506×2+1})$,即$(2^{1012},2^{1013})$。
17 [2025上海静安区期中]已知正比例函数$y= kx$的图象经过点A,点A在第四象限,过点A作$AH⊥x$轴,垂足为点H,点A的横坐标为3,且$\triangle AOH$的面积为3(O为坐标原点)。
(1)求正比例函数的表达式。
(2)在x轴上是否存在一点P,使$\triangle AOP$的面积为5? 若存在,求点P的坐标;若不存在,请说明理由。
(3)在(2)的条件下,在正比例函数$y= kx$的图象上是否存在一点M,使得$S_{\triangle APM}= \frac {2}{3}S_{\triangle OPM}$?若存在,请求出点M的坐标;若不存在,请说明理由。
(1)求正比例函数的表达式。
(2)在x轴上是否存在一点P,使$\triangle AOP$的面积为5? 若存在,求点P的坐标;若不存在,请说明理由。
(3)在(2)的条件下,在正比例函数$y= kx$的图象上是否存在一点M,使得$S_{\triangle APM}= \frac {2}{3}S_{\triangle OPM}$?若存在,请求出点M的坐标;若不存在,请说明理由。
答案:
解:(1)因为点$A$的横坐标为3,且$\triangle AOH$的面积为3,
所以$\frac{1}{2}×3×AH=3$,解得$AH=2$,
所以点$A$的坐标为$(3,-2)$,
因为正比例函数$y=kx$的图象经过点$A$,
所以$3k=-2$,解得$k=-\frac{2}{3}$,
所以正比例函数的表达式是$y=-\frac{2}{3}x$。
(2)存在。
设$P(t,0)$,因为$\triangle AOP$的面积为5,点$A$的坐标为$(3,-2)$,
所以$\frac{1}{2}×|t|×2=5$,所以$t=5$或$t=-5$,
所以点$P$的坐标为$(5,0)$或$(-5,0)$。
(3)存在。
设$M(x,-\frac{2}{3}x)$,
①若点$M$在线段$OA$上,如图1,当$P$的坐标为$(5,0)$时,$OP=5$,
因为$A(3,-2)$,$S_{\triangle APM}=\frac{2}{3}S_{\triangle OPM}$,
所以$\frac{1}{2}×OP×|y_{A}|-\frac{1}{2}×OP×|y_{M}|=\frac{2}{3}×\frac{1}{2}×OP×|y_{M}|$,
所以$\frac{1}{2}×5×2-\frac{1}{2}×5×\frac{2}{3}x=\frac{2}{3}×\frac{1}{2}×5×\frac{2}{3}x$,解得$x=\frac{9}{5}$,
所以$-\frac{2}{3}x=-\frac{2}{3}×\frac{9}{5}=-\frac{6}{5}$,所以点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$。
当点$P$的坐标为$(-5,0)$时,$OP=5$,同理可得点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$。
②若点$M$在线段$OA$的延长线上,如图2,当$P$的坐标为$(5,0)$时,$OP=5$,
因为$A(3,-2)$,$S_{\triangle APM}=\frac{2}{3}S_{\triangle OPM}$,
所以$\frac{1}{2}×OP×|y_{M}|-\frac{1}{2}×OP×|y_{A}|=\frac{2}{3}×\frac{1}{2}×OP×|y_{M}|$,
所以$\frac{1}{2}×5×\frac{2}{3}x-\frac{1}{2}×5×2=\frac{2}{3}×\frac{1}{2}×5×\frac{2}{3}x$,解得$x=9$,
所以$-\frac{2}{3}x=-\frac{2}{3}×9=-6$,所以点$M$的坐标为$(9,-6)$。
当点$P$的坐标为$(-5,0)$时,$OP=5$,同理可得点$M$的坐标为$(9,-6)$。
综上,点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$或$(9,-6)$。


解:(1)因为点$A$的横坐标为3,且$\triangle AOH$的面积为3,
所以$\frac{1}{2}×3×AH=3$,解得$AH=2$,
所以点$A$的坐标为$(3,-2)$,
因为正比例函数$y=kx$的图象经过点$A$,
所以$3k=-2$,解得$k=-\frac{2}{3}$,
所以正比例函数的表达式是$y=-\frac{2}{3}x$。
(2)存在。
设$P(t,0)$,因为$\triangle AOP$的面积为5,点$A$的坐标为$(3,-2)$,
所以$\frac{1}{2}×|t|×2=5$,所以$t=5$或$t=-5$,
所以点$P$的坐标为$(5,0)$或$(-5,0)$。
(3)存在。
设$M(x,-\frac{2}{3}x)$,
①若点$M$在线段$OA$上,如图1,当$P$的坐标为$(5,0)$时,$OP=5$,
因为$A(3,-2)$,$S_{\triangle APM}=\frac{2}{3}S_{\triangle OPM}$,
所以$\frac{1}{2}×OP×|y_{A}|-\frac{1}{2}×OP×|y_{M}|=\frac{2}{3}×\frac{1}{2}×OP×|y_{M}|$,
所以$\frac{1}{2}×5×2-\frac{1}{2}×5×\frac{2}{3}x=\frac{2}{3}×\frac{1}{2}×5×\frac{2}{3}x$,解得$x=\frac{9}{5}$,
所以$-\frac{2}{3}x=-\frac{2}{3}×\frac{9}{5}=-\frac{6}{5}$,所以点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$。
当点$P$的坐标为$(-5,0)$时,$OP=5$,同理可得点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$。
②若点$M$在线段$OA$的延长线上,如图2,当$P$的坐标为$(5,0)$时,$OP=5$,
因为$A(3,-2)$,$S_{\triangle APM}=\frac{2}{3}S_{\triangle OPM}$,
所以$\frac{1}{2}×OP×|y_{M}|-\frac{1}{2}×OP×|y_{A}|=\frac{2}{3}×\frac{1}{2}×OP×|y_{M}|$,
所以$\frac{1}{2}×5×\frac{2}{3}x-\frac{1}{2}×5×2=\frac{2}{3}×\frac{1}{2}×5×\frac{2}{3}x$,解得$x=9$,
所以$-\frac{2}{3}x=-\frac{2}{3}×9=-6$,所以点$M$的坐标为$(9,-6)$。
当点$P$的坐标为$(-5,0)$时,$OP=5$,同理可得点$M$的坐标为$(9,-6)$。
综上,点$M$的坐标为$(\frac{9}{5},-\frac{6}{5})$或$(9,-6)$。


查看更多完整答案,请扫码查看


