第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 在分组时要求“组内离差平方和最小”,其目的是 (
A. 使每组数据量相等
B. 使每组组内数据差异尽可能小,组间数据差异尽可能大
C. 减少计算复杂度
D. 保证组间均值相等
B
)A. 使每组数据量相等
B. 使每组组内数据差异尽可能小,组间数据差异尽可能大
C. 减少计算复杂度
D. 保证组间均值相等
答案:
B 组内离差平方和反映组内数据波动程度,最小化该值可使每组组内数据差距不大,同时组间数据差异明显。
2 [2024 云南中考]甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人 10 次射击成绩的平均数$\overline {x}$(单位:环)和方差$s^{2}$如表所示:
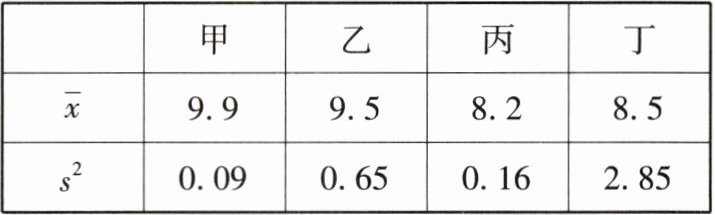
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (
A. 甲
B. 乙
C. 丙
D. 丁

根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (
A
)A. 甲
B. 乙
C. 丙
D. 丁
答案:
A 由题中表格可知,甲、乙的平均数较大,甲、丙的方差较小,所以应该选择甲参加比赛。
3 [2024 杭州建兰中学期中]体育委员小聪要帮体育老师分析本班的跳远成绩,将各统计量计算好后却发现由于场地布置失误,导致每位同学的成绩都少记录了 3 cm,则实际成绩与记录成绩相比,方差 (
A. 不变
B. 变大
C. 变小
D. 不能确定
A
)A. 不变
B. 变大
C. 变小
D. 不能确定
答案:
A
归纳总结
设 n 个数据 $ x_1, x_2, \cdots, x_n $ 的平均数为 a,方差为 b,则数据 $ x_1 + m, x_2 + m, \cdots, x_n + m $ 的平均数为 $ a + m $,方差为 b。
归纳总结
设 n 个数据 $ x_1, x_2, \cdots, x_n $ 的平均数为 a,方差为 b,则数据 $ x_1 + m, x_2 + m, \cdots, x_n + m $ 的平均数为 $ a + m $,方差为 b。
4 新考法 [2025 新乡一模]社会主义本质是解放生产力,发展生产力,消灭剥削,消除两极分化,最终达到共同富裕。下列有关居民收入的统计量中,最能体现发展生产力,消除两极分化的是 (
A. 收入平均数变小,方差变大
B. 收入平均数变小,方差变小
C. 收入平均数变大,方差变大
D. 收入平均数变大,方差变小
D
)A. 收入平均数变小,方差变大
B. 收入平均数变小,方差变小
C. 收入平均数变大,方差变大
D. 收入平均数变大,方差变小
答案:
D
5 教材例题变式 某小组 8 名学生的数学考试成绩(单位:分)分别为 88,98,87,92,92,90,91,96。老师决定将这些成绩分为两组,以便更好地分析学生的成绩分布。若按照以下分组方式:第一组$\{ 87,88,90,91,92,92\}$,第二组$\{ 96,98\}$。则组内离差平方和为
24
。
答案:
24 第一组有 6 个数据 $ \{87, 88, 90, 91, 92, 92\} $,这 6 个数据的平均数是 90,故第一组数据的组内离差平方和 $ S_1 = (87 - 90)^2 + (88 - 90)^2 + (90 - 90)^2 + (91 - 90)^2 + (92 - 90)^2 + (92 - 90)^2 = 22 $;第二组有 2 个数据 $ \{96, 98\} $,这 2 个数据的平均数是 97,故第二组数据的组内离差平方和 $ S_2 = (96 - 97)^2 + (98 - 97)^2 = 2 $。所以这种分组情况的组内离差平方和 $ S = S_1 + S_2 = 22 + 2 = 24 $。
6 甲、乙两名同学参加学校组织的 100 米短跑集训,教练把 10 天的训练成绩用折线图(如图)进行了统计。

(1)请你用折线图所提供的信息完成下表:
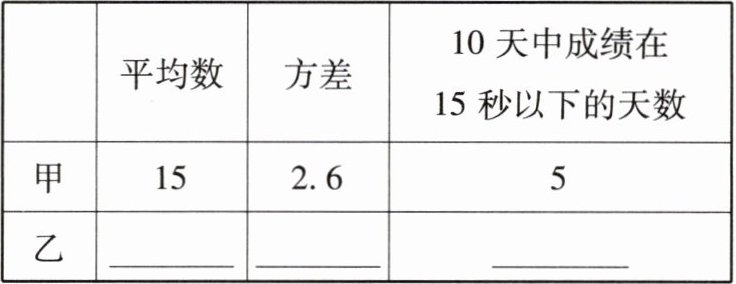
(2)学校欲从两人中选出一人参加市中学生运动会 100 米比赛,请你帮助学校做出选择,并简述你的理由。

(1)请你用折线图所提供的信息完成下表:

(2)学校欲从两人中选出一人参加市中学生运动会 100 米比赛,请你帮助学校做出选择,并简述你的理由。
如果学校要求成绩稳定,应选乙,因为甲和乙平均成绩相同,乙的方差小于甲的方差,所以在平均成绩相同的情况下乙的成绩比甲的成绩稳定;如果学校想夺冠,应选甲,因为 10 天中甲的成绩在 15 秒以下的天数比乙多,所以夺冠的可能性大。(答案不唯一,合理即可)
答案:
解:
(1) 填表如下:
| | 平均数 | 方差 | 10 天中成绩在 15 秒以下的天数 |
| --- | --- | --- | --- |
| 甲 | 15 | 2.6 | 5 |
| 乙 | | | |
$ \overline{x}_乙 = \frac{1}{10} \times (17 + 16 + 15 + 15 + 14 + 15 + 14 + 14 + 15 + 15) = 15 $,$ s^2_乙 = \frac{1}{10} \times [(17 - 15)^2 + (16 - 15)^2 + 5 \times (15 - 15)^2 + 3 \times (14 - 15)^2] = 0.8 $,由题图易知乙 10 天中成绩在 15 秒以下的有 3 天。
(2) 如果学校要求成绩稳定,应选乙,因为 $ \overline{x}_甲 = \overline{x}_乙 $,$ s^2_甲 > s^2_乙 $,所以在平均成绩相同的情况下乙的成绩比甲的成绩稳定;
如果学校想夺冠,应选甲,因为 10 天中甲的成绩在 15 秒以下的天数比乙多,所以夺冠的可能性大。(答案不唯一,合理即可)
(1) 填表如下:
| | 平均数 | 方差 | 10 天中成绩在 15 秒以下的天数 |
| --- | --- | --- | --- |
| 甲 | 15 | 2.6 | 5 |
| 乙 | | | |
$ \overline{x}_乙 = \frac{1}{10} \times (17 + 16 + 15 + 15 + 14 + 15 + 14 + 14 + 15 + 15) = 15 $,$ s^2_乙 = \frac{1}{10} \times [(17 - 15)^2 + (16 - 15)^2 + 5 \times (15 - 15)^2 + 3 \times (14 - 15)^2] = 0.8 $,由题图易知乙 10 天中成绩在 15 秒以下的有 3 天。
(2) 如果学校要求成绩稳定,应选乙,因为 $ \overline{x}_甲 = \overline{x}_乙 $,$ s^2_甲 > s^2_乙 $,所以在平均成绩相同的情况下乙的成绩比甲的成绩稳定;
如果学校想夺冠,应选甲,因为 10 天中甲的成绩在 15 秒以下的天数比乙多,所以夺冠的可能性大。(答案不唯一,合理即可)
查看更多完整答案,请扫码查看


