第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 [2024泸州中考]下列各数中,无理数是(
A. $-\frac{1}{3}$
B. 3.14
C. 0
D. $\pi$
D
)A. $-\frac{1}{3}$
B. 3.14
C. 0
D. $\pi$
答案:
D $-\frac{1}{3}$是分数,3.14 是有限小数,0 是整数,它们都不是无理数;π 是无限不循环小数,它是无理数。
归纳总结
常见的无理数的类型
(1)无限不循环小数;
(2)含 π 的数;
(3)人为构造的有特定结构,但不循环的小数。
归纳总结
常见的无理数的类型
(1)无限不循环小数;
(2)含 π 的数;
(3)人为构造的有特定结构,但不循环的小数。
2 [2025北京五十四中期末]给出下列各数:$-8,2.7,-3\frac{1}{2},\frac{\pi}{3},0.66666…,0.2,0.080080008…$。其中无理数的个数为(
A. 0
B. 1
C. 2
D. 3
C
)A. 0
B. 1
C. 2
D. 3
答案:
C $\frac{\pi}{3}$,0.080 080 008…是无理数。
归纳总结
有理数和无理数的区别
(1)无理数是无限不循环小数,有理数是有限小数或无限循环小数;
(2)有理数可以化为分数,无理数不能化为分数。
归纳总结
有理数和无理数的区别
(1)无理数是无限不循环小数,有理数是有限小数或无限循环小数;
(2)有理数可以化为分数,无理数不能化为分数。
3 新趋势·结论开放[2025盐城期中]请你写出一个无理数a,使得$0 < a < 1$,则a为
$\frac{\pi}{4}$
。(写出一个即可)
答案:
(答案不唯一)$\frac{\pi}{4}$
4 [2024承德期中]下列说法中,正确的是(
A. 无理数包括正无理数、零和负无理数
B. 无限小数都是无理数
C. 正实数包括正有理数和正无理数
D. 实数可以分为正实数和负实数两类
C
)A. 无理数包括正无理数、零和负无理数
B. 无限小数都是无理数
C. 正实数包括正有理数和正无理数
D. 实数可以分为正实数和负实数两类
答案:
C 无理数包括正无理数和负无理数,故 A 项错误;无限循环小数是有理数,无限不循环小数是无理数,故 B 项错误;实数可分为正实数、零和负实数三类,故 D 项错误。
5 教材习题变式 把下列实数分别填入相应的集合里:$-|-5|,|-\frac{3}{2}|,0,-3.14,\frac{22}{7},1.99,-(-6),2\pi,-12.101001…$(每两个1之间0的个数依次增加1)。
(1)负数集合:…$\{\}$。
(2)非负整数集合:…$\{\}$。
(3)分数集合:…$\{\}$。
(4)无理数集合:…$\{\}$。
(1)负数集合:…$\{\}$。
(2)非负整数集合:…$\{\}$。
(3)分数集合:…$\{\}$。
(4)无理数集合:…$\{\}$。
答案:
解:$-|-5|=-5$,$|-\frac{3}{2}|=\frac{3}{2}$,$-(-6)=6$。
(1)负数集合:$\{-|-5|,-3.14,-12.101 001…$(每两个 1 之间 0 的个数依次增加 1)$\cdots\}$。
(2)非负整数集合:$\{0,-(-6)\cdots\}$。
(3)分数集合:$\{|-\frac{3}{2}|,-3.14,\frac{22}{7},1.99\cdots\}$。
(4)无理数集合:$\{2\pi,-12.101 001…$(每两个 1 之间 0 的个数依次增加 1)$\cdots\}$。
(1)负数集合:$\{-|-5|,-3.14,-12.101 001…$(每两个 1 之间 0 的个数依次增加 1)$\cdots\}$。
(2)非负整数集合:$\{0,-(-6)\cdots\}$。
(3)分数集合:$\{|-\frac{3}{2}|,-3.14,\frac{22}{7},1.99\cdots\}$。
(4)无理数集合:$\{2\pi,-12.101 001…$(每两个 1 之间 0 的个数依次增加 1)$\cdots\}$。
6 [2025茂名电白区一模]π的绝对值是(
A. $\pi$
B. $-\pi$
C. $\pm \pi$
D. $\frac{1}{\pi}$
A
)A. $\pi$
B. $-\pi$
C. $\pm \pi$
D. $\frac{1}{\pi}$
答案:
A
7 [2024邵阳期中]已知$ab = 1$,若$a = 2024$,则b的相反数是(
A. -2024
B. $-\frac{1}{2024}$
C. $\frac{1}{2024}$
D. 2024
$-\frac{1}{2024}$
)A. -2024
B. $-\frac{1}{2024}$
C. $\frac{1}{2024}$
D. 2024
答案:
B 因为$ab = 1$,$a = 2024$,所以$b=\frac{1}{2024}$,所以 b 的相反数是$-\frac{1}{2024}$。
8 [2025宝鸡期中]已知实数a,b,c,d,e,且a,b互为倒数,c,d互为相反数,e的绝对值为2,求$\frac{1}{2}× ab+\frac{c + d}{5}-e$的值。
答案:
解:由题意,得$ab = 1$,$c + d = 0$,$e=\pm2$。
分两种情况:
当$e = 2$时,$\frac{1}{2}\times ab+\frac{c + d}{5}-e=\frac{1}{2}\times1+\frac{0}{5}-2=\frac{1}{2}-2=-\frac{3}{2}$。
当$e = -2$时,$\frac{1}{2}\times ab+\frac{c + d}{5}-e=\frac{1}{2}\times1+\frac{0}{5}+2=\frac{1}{2}+2=\frac{5}{2}$。
综上所述,$\frac{1}{2}\times ab+\frac{c + d}{5}-e$的值为$-\frac{3}{2}$或$\frac{5}{2}$。
分两种情况:
当$e = 2$时,$\frac{1}{2}\times ab+\frac{c + d}{5}-e=\frac{1}{2}\times1+\frac{0}{5}-2=\frac{1}{2}-2=-\frac{3}{2}$。
当$e = -2$时,$\frac{1}{2}\times ab+\frac{c + d}{5}-e=\frac{1}{2}\times1+\frac{0}{5}+2=\frac{1}{2}+2=\frac{5}{2}$。
综上所述,$\frac{1}{2}\times ab+\frac{c + d}{5}-e$的值为$-\frac{3}{2}$或$\frac{5}{2}$。
9 [2025哈尔滨期末]与数轴上的点具有一一对应关系的数是(
A. 实数
B. 有理数
C. 无理数
D. 整数
A
)A. 实数
B. 有理数
C. 无理数
D. 整数
答案:
A
归纳总结
实数和数轴上的点“一一对应”的两层含义
实数和数轴上的点是一一对应的。“一一对应”包含两层含义:每一个实数都可以用数轴上的一个点来表示;数轴上的每一个点都表示一个实数。
归纳总结
实数和数轴上的点“一一对应”的两层含义
实数和数轴上的点是一一对应的。“一一对应”包含两层含义:每一个实数都可以用数轴上的一个点来表示;数轴上的每一个点都表示一个实数。
10 一题多解[2023新乡期末]实数a在数轴上的对应点的位置如图所示,若实数b满足$-a < b < a$,则b的值可以是(
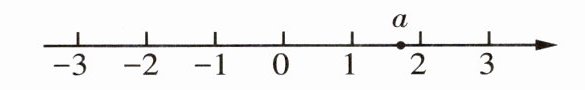
A. 2
B. -1
C. -2
D. -3
B
)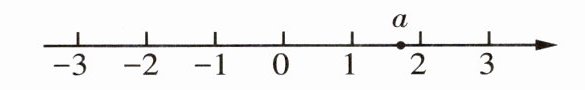
A. 2
B. -1
C. -2
D. -3
答案:
B 通解 因为$-a < b < a$,所以$|b| < a$,又因为$1 < a < 2$,所以 b 可以是 -1。
另解 因为$|a| < 2$,$-a < b < a$,所以实数 b 对应的点到原点的距离一定小于 2。
另解 因为$|a| < 2$,$-a < b < a$,所以实数 b 对应的点到原点的距离一定小于 2。
11 [2024北京中考]实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是(
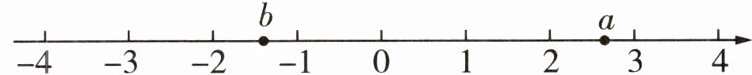
A. $b > -1$
B. $|b| > 2$
C. $a + b > 0$
D. $ab > 0$
C
)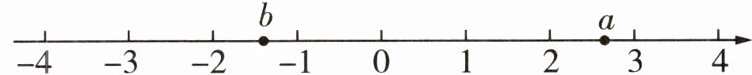
A. $b > -1$
B. $|b| > 2$
C. $a + b > 0$
D. $ab > 0$
答案:
C 由题中数轴可知,$-2 < b < -1$,$2 < a < 3$,所以$|b| < 2$,$a + b > 0$,$ab < 0$。
12 [2025石家庄五十四中期中]如图,半径为1个单位长度的圆上有一点A与数轴上表示-1的点重合,若将该圆沿数轴向右滚动一周,圆上的点A恰好与数轴上的点B重合,则点B对应的实数为(
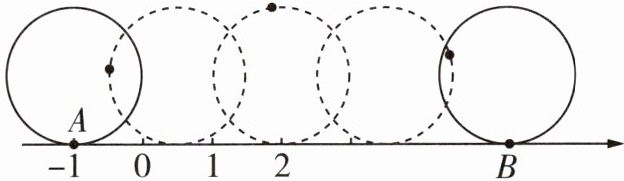
A. $\pi - 1$
B. $\pi + 1$
C. $2\pi - 1$
D. $2\pi + 1$
2π - 1
)
A. $\pi - 1$
B. $\pi + 1$
C. $2\pi - 1$
D. $2\pi + 1$
答案:
C 因为半径为 1 个单位长度的圆从表示 -1 的点沿数轴向右滚动一周,所以 AB 之间的距离为圆的周长,即$2\pi$,点 B 在数轴上表示 -1 的点的右侧,所以点 B 对应的数是$2\pi - 1$。
有理数和无理数有什么区别?
答案:
【解析】:有理数和无理数存在多方面的区别。从定义上看,有理数是整数(正整数、0、负整数)和分数的统称,也就是可以表示为两个整数之比的数;而无理数是无限不循环小数,不能表示为两个整数之比。从小数形式上,有理数包括有限小数和无限循环小数,有限小数可以很直观地看出其数值,无限循环小数有循环节,例如0.333… (3循环);无理数是无限不循环的,没有循环规律,像圆周率π约等于3.1415926… ,它的小数位是无限且不循环的。从性质上,有理数进行加、减、乘、除(除数不为0)运算后结果还是有理数;而无理数与有理数进行四则运算时,结果可能是无理数也可能是有理数,例如π + 1还是无理数,而$\sqrt{2}-\sqrt{2}=0$是有理数。从集合角度,有理数集是可数集,意味着可以与自然数集建立一一对应关系;无理数集是不可数集,其元素数量比有理数集多得多。
【答案】:1.定义:有理数是整数和分数的统称,能表示为两个整数之比;无理数是无限不循环小数,不能表示为两个整数之比。2.小数形式:有理数是有限小数或无限循环小数;无理数是无限不循环小数。3.运算性质:有理数进行四则运算(除数不为0)结果是有理数;无理数与有理数四则运算结果可能是无理数或有理数。4.集合特性:有理数集是可数集,无理数集是不可数集。
【答案】:1.定义:有理数是整数和分数的统称,能表示为两个整数之比;无理数是无限不循环小数,不能表示为两个整数之比。2.小数形式:有理数是有限小数或无限循环小数;无理数是无限不循环小数。3.运算性质:有理数进行四则运算(除数不为0)结果是有理数;无理数与有理数四则运算结果可能是无理数或有理数。4.集合特性:有理数集是可数集,无理数集是不可数集。
查看更多完整答案,请扫码查看


