第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
13 [2025亳州期中]已知点$P(2a,1-3a)$在第二象限,且点P到x轴的距离与到y轴的距离之和是11,则a的值为 (
A. -1
B. 1
C. -2
D. 3
C
)A. -1
B. 1
C. -2
D. 3
答案:
C 因为点P(2a,1-3a)在第二象限,所以2a<0,1-3a>0,所以点P到x轴的距离为|1-3a|=1-3a,到y轴的距离为|2a|=-2a。由题意,得1-3a-2a=11,解得a=-2。
14 新考法[2025郑州四中月考]如图,在平面直角坐标系中,点A的坐标为$(-1,3)$,点B的坐标为$(4,3)$,则线段AB上任意一点的坐标可表示为 (
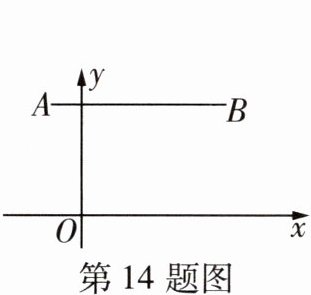
A. $(x,3)(-1≤x≤4)$
B. $(x,3)(x≤4)$
C. $(x,3)(x≥-1)$
D. $(x,3)$
(x,3)(-1≤x≤4)
)
A. $(x,3)(-1≤x≤4)$
B. $(x,3)(x≤4)$
C. $(x,3)(x≥-1)$
D. $(x,3)$
答案:
A 因为点A的坐标为(-1,3),点B的坐标为(4,3),A,B两点的纵坐标都为3,所以AB//x轴,所以线段AB上任意一点的坐标可表示为(x,3)(-1≤x≤4)。
15 [2025宁波鄞州区期末]如图,在平面直角坐标系中,$AB= AC= 13$,点B,C的坐标分别为$(7,2),(7,12)$,则点A的坐标为 ( )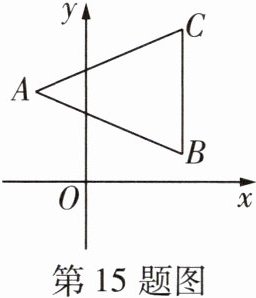
A. $(-5,5)$
B. $(-5,7)$
C. $(-7,5)$
D. $(-7,-7)$

A. $(-5,5)$
B. $(-5,7)$
C. $(-7,5)$
D. $(-7,-7)$
答案:
B 如图,过点A作AD⊥BC于点D,由条件可知BC=10,BC//y轴,因为AB=AC=13,所以BD=CD=1/2 BC=5,所以D((7+7)/2,(12+2)/2),即D(7,7),所以AD//x轴,即点A的纵坐标为7,因为AD=√(AB² - BD²)=√(13² - 5²)=12,所以点A的横坐标为7-12=-5,所以点A的坐标为(-5,7)。

B 如图,过点A作AD⊥BC于点D,由条件可知BC=10,BC//y轴,因为AB=AC=13,所以BD=CD=1/2 BC=5,所以D((7+7)/2,(12+2)/2),即D(7,7),所以AD//x轴,即点A的纵坐标为7,因为AD=√(AB² - BD²)=√(13² - 5²)=12,所以点A的横坐标为7-12=-5,所以点A的坐标为(-5,7)。

一题练透
点的坐
已知平面直角坐标系中有一点$P(m-1,2m+3)$。
(1)若点P在x轴上,则点P的坐标为
(2)若点P在第二、四象限的角平分线上,则点P的坐标为
(3)若点P到y轴的距离为2,求点P的坐标;
(4)若点P和点Q都在过点$M(2,3)$且与y轴平行的直线上,$PQ= 3$,求点Q的坐标。
点的坐
已知平面直角坐标系中有一点$P(m-1,2m+3)$。
(1)若点P在x轴上,则点P的坐标为
(-5/2,0)
; (2)若点P在第二、四象限的角平分线上,则点P的坐标为
(-5/3,5/3)
; (3)若点P到y轴的距离为2,求点P的坐标;
(4)若点P和点Q都在过点$M(2,3)$且与y轴平行的直线上,$PQ= 3$,求点Q的坐标。
答案:
(1)(-5/2,0)
由题意,得2m+3=0,解得m=-3/2,所以m-1=-5/2,所以点P的坐标为(-5/2,0)。
(2)(-5/3,5/3)
由题意,得(m-1)+(2m+3)=0,解得m=-2/3,所以m-1=-5/3,2m+3=5/3,所以点P的坐标为(-5/3,5/3)。
(3)由题意,得|m-1|=2,所以m=3或m=-1,
所以m-1=2,2m+3=9或m-1=-2,2m+3=1,
所以点P的坐标为(2,9)或(-2,1)。
(4)因为点P在过点M(2,3)且与y轴平行的直线上,
所以点P的横坐标为2,即m-1=2,解得m=3,
所以2m+3=9,所以点P的坐标为(2,9)。
因为点Q在过点M(2,3)且与y轴平行的直线上,
所以点Q的横坐标为2。
又因为PQ=3,所以当点Q在点P上方时,点Q的纵坐标为12;当点Q在点P下方时,点Q的纵坐标为6。
综上,点Q的坐标为(2,12)或(2,6)。
(1)(-5/2,0)
由题意,得2m+3=0,解得m=-3/2,所以m-1=-5/2,所以点P的坐标为(-5/2,0)。
(2)(-5/3,5/3)
由题意,得(m-1)+(2m+3)=0,解得m=-2/3,所以m-1=-5/3,2m+3=5/3,所以点P的坐标为(-5/3,5/3)。
(3)由题意,得|m-1|=2,所以m=3或m=-1,
所以m-1=2,2m+3=9或m-1=-2,2m+3=1,
所以点P的坐标为(2,9)或(-2,1)。
(4)因为点P在过点M(2,3)且与y轴平行的直线上,
所以点P的横坐标为2,即m-1=2,解得m=3,
所以2m+3=9,所以点P的坐标为(2,9)。
因为点Q在过点M(2,3)且与y轴平行的直线上,
所以点Q的横坐标为2。
又因为PQ=3,所以当点Q在点P上方时,点Q的纵坐标为12;当点Q在点P下方时,点Q的纵坐标为6。
综上,点Q的坐标为(2,12)或(2,6)。
16 [2025平顶山期中]若点$A(x,y)的坐标满足等式x+y-xy= 0$,则称该点A为“和谐点”。若某个“和谐点”到x轴的距离为4,则该点的坐标为 (
A. $(\frac {4}{3},4)或(2,2)$
B. $(\frac {4}{5},-4)或(\frac {4}{3},4)$
C. $(\frac {4}{5},-2)或(-2,-2)$
D. $(\frac {4}{5},4)或(-\frac {4}{3},-4)$
(4/3,4)或(4/5,-4)
)A. $(\frac {4}{3},4)或(2,2)$
B. $(\frac {4}{5},-4)或(\frac {4}{3},4)$
C. $(\frac {4}{5},-2)或(-2,-2)$
D. $(\frac {4}{5},4)或(-\frac {4}{3},-4)$
答案:
B 因为到x轴的距离为4,所以y=4或y=-4,当y=4时,x+y-xy=x+4-4x=0,解得x=4/3,所以该点的坐标为(4/3,4);当y=-4时,x+y-xy=x-4+4x=0,解得x=4/5,所以该点的坐标为(4/5,-4)。
17 [2024咸阳彩虹中学期中]在平面直角坐标系中,点$A(-2,3),B(1,-4)$,经过点A的直线$l// y$轴,若点C为直线l上的一个动点,则当线段BC的长度最小时,点C的坐标为
(-2,-4)
。
答案:
(-2,-4) 由垂线段最短,知当BC⊥l时,线段BC的长度最小。因为l//y轴,所以当BC⊥l时,BC//x轴,所以点C的纵坐标和点B的纵坐标相同。因为点A和点C都在直线l上,所以点C的横坐标和点A的横坐标相同,所以点C的坐标为(-2,-4)。
18 [2024沈阳期中]在平面直角坐标系中取任意两点$A(x_{1},y_{1}),B(x_{2},y_{2})$,定义新运算“*”,得到点C的坐标为$(x_{1}y_{2},x_{2}y_{1})$,即$(x_{1},y_{1})*(x_{2},y_{2})= (x_{1}y_{2},x_{2}y_{1})$。若点A在第一象限,点B在第四象限,根据上述规则得到的点C在第
二
象限。
答案:
二 因为点A(x₁,y₁)在第一象限,点B(x₂,y₂)在第四象限,所以x₁>0,y₁>0,x₂>0,y₂<0,所以x₁y₂<0,x₂y₁>0,所以点C在第二象限。
在平面直角坐标系中,如何确定给定点的坐标?
给定点的坐标,如何确定对应的点?
给定点的坐标,如何确定对应的点?
答案:
【解析】:1. 确定平面直角坐标系中给定点的坐标:过该点分别向$x$轴和$y$轴作垂线,垂足在$x$轴上对应的数就是该点的横坐标,垂足在$y$轴上对应的数就是该点的纵坐标,横坐标写在前,纵坐标写在后,中间用逗号隔开,并用小括号括起来,即为该点的坐标。
2. 已知点的坐标确定对应的点:先在$x$轴上找到横坐标对应的位置,过该位置作$x$轴的垂线;再在$y$轴上找到纵坐标对应的位置,过该位置作$y$轴的垂线,这两条垂线的交点就是该坐标对应的点。
【答案】:1. 过该点分别向$x$轴和$y$轴作垂线,垂足在$x$轴、$y$轴上对应的数分别为横坐标、纵坐标,用$(横坐标,纵坐标)$表示该点坐标。 2. 先在$x$轴上找到横坐标对应的位置作$x$轴垂线,在$y$轴上找到纵坐标对应的位置作$y$轴垂线,两垂线交点即为对应点。
2. 已知点的坐标确定对应的点:先在$x$轴上找到横坐标对应的位置,过该位置作$x$轴的垂线;再在$y$轴上找到纵坐标对应的位置,过该位置作$y$轴的垂线,这两条垂线的交点就是该坐标对应的点。
【答案】:1. 过该点分别向$x$轴和$y$轴作垂线,垂足在$x$轴、$y$轴上对应的数分别为横坐标、纵坐标,用$(横坐标,纵坐标)$表示该点坐标。 2. 先在$x$轴上找到横坐标对应的位置作$x$轴垂线,在$y$轴上找到纵坐标对应的位置作$y$轴垂线,两垂线交点即为对应点。
查看更多完整答案,请扫码查看


