《2025年一遍过八年级数学上册北师大版》

1 [2025重庆沙坪坝区期末]在一场赛车比赛中,有两辆赛车甲和乙同时出发,赛车行驶过程中,随着时间推移,赛车的能量值会不断消耗。如图,线段AC表示甲车,线段AB表示乙车,在这段时间内,甲、乙两车的能量值y(单位)与行驶时间x(分)之间都近似满足一次函数关系,其函数图象如图所示。根据图象信息,下列说法不正确的是 (B)

A. 甲、乙两车的初始能量值均为90单位
B. 甲车能量消耗更慢
C. 乙车的能量值y与行驶时间x的函数关系式为$y= -\frac {1}{10}x+90$
D. 当甲车的能量值是60单位时,乙车的能量值是75单位

答案： B 观察题中图象，AB，AC与y轴交点的纵坐标均为90，即甲、乙两车的初始能量值均为90单位，A项正确；当x=300时，甲车剩余能量为30单位，乙车剩余能量为60单位，所以乙车能量消耗更慢，B项不正确；设乙车的能量值y与行驶时间x的函数关系式为y=kx+b（k，b为常数，且k≠0），则b=90，300k+b=60，所以k=- $\frac{1}{10}$，所以乙车的能量值y与行驶时间x的函数关系式为y=- $\frac{1}{10}$x+90，C项正确；当甲车的能量值是60单位时，x=150，当x=150时，y=- $\frac{1}{10}$×150+90=75，所以当甲车的能量值是60单位时，乙车的能量值是75单位，D项正确。

2 [新趋势·数学文化[2024烟台期末]《九章算术》记载:今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺。问几何日相逢。意思是:有一道墙,高9尺,墙顶长了一株瓜,瓜蔓向下伸,每天长7寸(1尺= 10寸);墙脚长着瓠,瓠蔓每天长1尺,问瓜蔓、瓠蔓要多少天才相遇。如图是瓜蔓与瓠蔓离地面的高度h(尺)关于生长时间x(天)的函数图象,则由图可知两图象交点P的横坐标是 ($\frac{90}{17}$)
A. $\frac {9}{2}$
B. 5
C. $\frac {90}{17}$
D. 6

答案： C 7寸=0.7尺。因为瓜蔓在高9尺的墙上向下伸，每天长7寸，所以x天时瓜蔓的高度h₁=9-0.7x。因为瓠蔓向上长，每天长1尺，所以x天时高度h₂=x。因为相遇时高度相等，所以9-0.7x=x，解得x= $\frac{90}{17}$。所以两图象交点P的横坐标为 $\frac{90}{17}$。

3 [2024西宁中考]西宁市城北客运站是我市“一芯双城”建设规划项目之一,依据规划要按一定比例配套建设新能源汽车充电设施。某校数学兴趣小组为了解新能源汽车的充电情况,对某品牌汽车进行了调查研究,绘制了如图所示的汽车电池电量y(单位:$kW\cdot h$)与充电时间x(单位:h)之间的函数图象,其中折线ABC表示用快速充电器充电时$y_{1}$与x的函数关系;线段AD表示用普通充电器充电时$y_{2}$与x的函数关系。根据相关信息,回答下列问题:
(1)用快速充电器充电时,汽车电池电量从$10kW\cdot h充到70kW\cdot h$需$\frac{1}{3}$h。
(2)求$y_{2}$关于x的函数表达式,并直接写出自变量x的取值范围。
(3)该品牌汽车电池电量从$10kW\cdot h充到100kW\cdot h$,快速充电器比普通充电器少用$\frac{7}{3}$h。

答案： 解：（1） $\frac{1}{3}$
（2）设y₂关于x的函数表达式为y₂=kx+b（k≠0），
将A(0,10)，E(2,70)的坐标代入，得 $\begin{cases}b=10,\\2k+b=70,\end{cases}$
解得 $\begin{cases}k=30,\\b=10,\end{cases}$
所以y₂关于x的函数表达式为y₂=30x+10（0≤x≤3）。
（3） $\frac{7}{3}$
把y₂=100代入y₂=30x+10，得30x+10=100，解得x=3，所以3- $\frac{2}{3}$ = $\frac{7}{3}$（h），即该品牌汽车电池电量从10kW·h充到100kW·h，快速充电器比普通充电器少用 $\frac{7}{3}$ h。

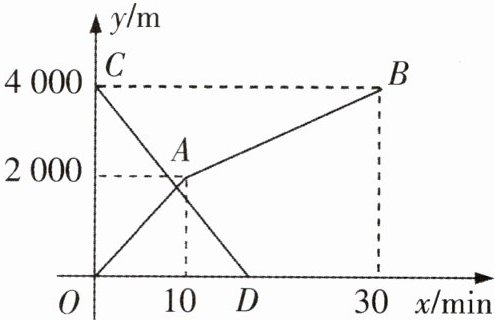
4 [2025北京育才学校模拟]小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行。小玲开始跑步中途改为步行,到达图书馆恰好用30min。小东骑自行车以$300m/min$的速度直接回家。两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数关系如图所示。
(1)家与图书馆之间的路程为4000m,小玲步行的速度为100m/min;
(2)求小东离家的路程y关于x的函数表达式,并写出自变量的取值范围;
(3)求两人相遇的时间。

答案： 解：（1）4000 100
结合题意和题中图象可知，线段CD为小东离家的路程与离开出发地的时间的函数图象，折线OAB为小玲离家的路程与离开出发地的时间的函数图象，则家与图书馆之间的路程为4000m，小玲步行的速度为（4000-2000）÷（30-10）=100（m/min）。
（2）因为小东从离家4000m的图书馆以300m/min的速度返回家，所以小东回家用的时间为4000÷300= $\frac{40}{3}$（min），所以D( $\frac{40}{3}$,0 )。
设直线CD的函数表达式为y=kx+b（k≠0），
因为y=kx+b的图象经过点(0,4000)，( $\frac{40}{3}$,0 )，
所以将(0,4000)代入，得b=4000，
将( $\frac{40}{3}$,0 )代入，得 $\frac{40}{3}$k+4000=0，
解得k=-300，
所以小东离家的路程y关于x的函数表达式为y=-300x+4000（0≤x≤ $\frac{40}{3}$ ）。
（3）由题中图象可知，两人相遇是在小玲跑步的过程中，
设小玲跑步的过程中，离家的路程y关于时间x的函数表达式为y=mx（m≠0），
将点A的坐标(10,2000)代入，得2000=10m，解得m=200，
所以y=200x。
两人相遇时，200x=-300x+4000，解得x=8，
故两人相遇的时间为离开出发地8min时。