第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 现有 8 张卡片,分别写上数字 2,4,5,5,6,7,9,16,则这 8 个数的上四分位数是
8
。
答案:
8
2 教材例题变式 [2025 邯郸一模改编]某校举办校园歌手大赛,决赛中 12 名参赛选手的得分(满分:10 分)分别为 9.5,8.1,7.8,8.5,8.8,9.1,7.5,9.6,8.6,8.8,9.3,9.0。求这组数据的四分位数 $ m_{25} $,$ m_{50} $,$ m_{75} $。
答案:
解:将这12个数据由小到大排序,得7.5,7.8,8.1,8.5,8.6,8.8,8.8,9.0,9.1,9.3,9.5,9.6,
中位数即50%分位数,因此$m_{50}=\frac{8.8 + 8.8}{2}=8.8$ (分);
前一半数据的中位数为整组数据的下四分位数,故
$m_{25}=\frac{8.1 + 8.5}{2}=8.3$ (分);
后一半数据的中位数为整组数据的上四分位数,故
$m_{75}=\frac{9.1 + 9.3}{2}=9.2$ (分)。
中位数即50%分位数,因此$m_{50}=\frac{8.8 + 8.8}{2}=8.8$ (分);
前一半数据的中位数为整组数据的下四分位数,故
$m_{25}=\frac{8.1 + 8.5}{2}=8.3$ (分);
后一半数据的中位数为整组数据的上四分位数,故
$m_{75}=\frac{9.1 + 9.3}{2}=9.2$ (分)。
3 [2024 潍坊模拟]有一组被墨水污染的数据:4,17,7,14,★,★,★,16,10,4,4,11,其箱线图如图所示:

下列说法不正确的是 (
A. 这组数据的下四分位数是 4
B. 这组数据的中位数是 10
C. 这组数据的上四位数是 15
D. 被墨水污染的数据中一个数是 3,一个数是 18

下列说法不正确的是 (
B
)A. 这组数据的下四分位数是 4
B. 这组数据的中位数是 10
C. 这组数据的上四位数是 15
D. 被墨水污染的数据中一个数是 3,一个数是 18
答案:
B 这组数据的下四分位数是4,上四位数是15,中位数为10.5,故A项、C项正确,B项不正确;箱线图的下边缘是3,上边缘是18,所以被墨水污染的数据中一个数是3,一个数是18,D项正确。
4 [2024 台州期末]如图是甲、乙两地在某一个月中日平均气温的箱线图,从中可以发现这个月的日平均气温方差较大的是
甲地
。(填“甲地”或“乙地”)
答案:
甲地 根据题中箱线图可知,甲地的日平均气温比乙地波动大,故甲地的日平均气温的方差大。
5 甲、乙两组的测试成绩如下:
甲:91,96,70,89,60,70,100,80,92,98。
乙:92,93,70,88,82,75,96,80,92,95。
(1)求甲组数据的四分位数 $ m_{25} $,$ m_{50} $,$ m_{75} $。
(2)根据四分位数可绘制如图所示的箱线图,观察图中乙组的箱线图,绘制甲组的箱线图。
(3)根据对箱线图和四分位数的理解,谈谈你对两组成绩的看法。
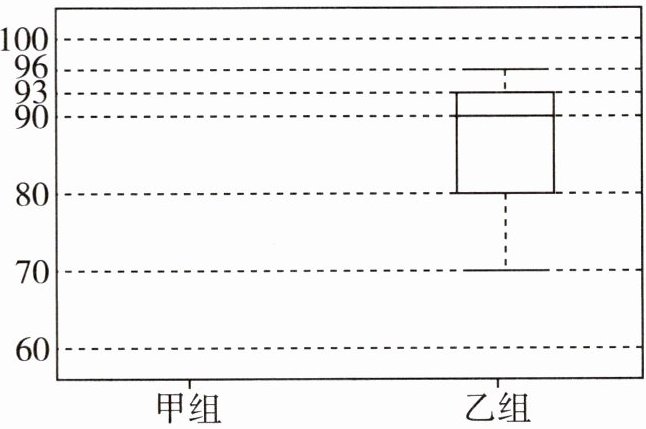
甲:91,96,70,89,60,70,100,80,92,98。
乙:92,93,70,88,82,75,96,80,92,95。
(1)求甲组数据的四分位数 $ m_{25} $,$ m_{50} $,$ m_{75} $。
(2)根据四分位数可绘制如图所示的箱线图,观察图中乙组的箱线图,绘制甲组的箱线图。
(3)根据对箱线图和四分位数的理解,谈谈你对两组成绩的看法。

答案:
解:
(1)把甲的成绩从小到大排列为60,70,70,80,89,91,92,96,98,100,
故$m_{50}=\frac{89 + 91}{2}=90,m_{25}=70,m_{75}=96$。
(2)绘制甲组的箱线图如图所示。
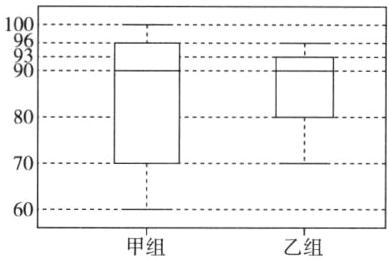
(3)(答案不唯一)根据箱线图和四分位数,可知甲组成绩比较分散,乙组成绩比较集中。
解:
(1)把甲的成绩从小到大排列为60,70,70,80,89,91,92,96,98,100,
故$m_{50}=\frac{89 + 91}{2}=90,m_{25}=70,m_{75}=96$。
(2)绘制甲组的箱线图如图所示。

(3)(答案不唯一)根据箱线图和四分位数,可知甲组成绩比较分散,乙组成绩比较集中。
刻画数据集中趋势的统计量有哪些?刻画数据离散程度的统计量有哪些?它们各有什么特点?
答案:
【解析】:
1. 首先明确刻画数据集中趋势的统计量:
平均数是一组数据的总和除以数据的个数,它利用了所有数据的信息,能反映一组数据的平均水平,但容易受极端值的影响。例如,在数据$1,2,3,4,100$中,平均数为$(1 + 2+3 + 4+100)\div5 = 22$,$100$这个极端值对平均数影响较大。
中位数是将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数为中位数;如果数据的个数是偶数,则中间两个数据的平均数为中位数。它不受极端值的影响,当数据中有极端值时,中位数能更好地反映数据的中间水平。比如数据$1,2,3,4,100$,中位数是$3$。
众数是一组数据中出现次数最多的数据值。它可以反映一组数据中出现次数最多的那个特征,可能不止一个,也可能没有。例如数据$1,2,2,3,3$,众数是$2$和$3$;数据$1,2,3,4,5$没有众数。
2. 然后明确刻画数据离散程度的统计量:
极差是一组数据中的最大值减去最小值,它计算简单,能反映数据的变化范围,但只考虑了最大值和最小值,对其他数据的波动情况反映不全面。例如数据$1,2,3,4,10$,极差为$10 - 1=9$。
方差是每个样本值与全体样本值的平均数之差的平方值的平均数。它反映了一组数据与其平均数的偏离程度,方差越大,数据的离散程度越大,稳定性越差;方差越小,数据的离散程度越小,稳定性越好。计算相对复杂,但能更全面地反映数据的离散情况。
标准差是方差的算术平方根,它和方差的作用类似,也是衡量数据离散程度的统计量,由于其单位与原数据单位一致,在实际应用中更便于理解和比较。
【答案】:
刻画数据集中趋势的统计量有平均数、中位数、众数。
特点:平均数利用了所有数据的信息,能反映一组数据的平均水平,但易受极端值影响;中位数不受极端值影响,能更好地反映数据的中间水平;众数可以反映一组数据中出现次数最多的特征,可能不止一个,也可能没有。
刻画数据离散程度的统计量有极差、方差、标准差。
特点:极差计算简单,能反映数据的变化范围,但对其他数据的波动情况反映不全面;方差反映了一组数据与其平均数的偏离程度,能更全面地反映数据的离散情况,但计算相对复杂;标准差和方差作用类似,单位与原数据单位一致,便于理解和比较。
1. 首先明确刻画数据集中趋势的统计量:
平均数是一组数据的总和除以数据的个数,它利用了所有数据的信息,能反映一组数据的平均水平,但容易受极端值的影响。例如,在数据$1,2,3,4,100$中,平均数为$(1 + 2+3 + 4+100)\div5 = 22$,$100$这个极端值对平均数影响较大。
中位数是将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数为中位数;如果数据的个数是偶数,则中间两个数据的平均数为中位数。它不受极端值的影响,当数据中有极端值时,中位数能更好地反映数据的中间水平。比如数据$1,2,3,4,100$,中位数是$3$。
众数是一组数据中出现次数最多的数据值。它可以反映一组数据中出现次数最多的那个特征,可能不止一个,也可能没有。例如数据$1,2,2,3,3$,众数是$2$和$3$;数据$1,2,3,4,5$没有众数。
2. 然后明确刻画数据离散程度的统计量:
极差是一组数据中的最大值减去最小值,它计算简单,能反映数据的变化范围,但只考虑了最大值和最小值,对其他数据的波动情况反映不全面。例如数据$1,2,3,4,10$,极差为$10 - 1=9$。
方差是每个样本值与全体样本值的平均数之差的平方值的平均数。它反映了一组数据与其平均数的偏离程度,方差越大,数据的离散程度越大,稳定性越差;方差越小,数据的离散程度越小,稳定性越好。计算相对复杂,但能更全面地反映数据的离散情况。
标准差是方差的算术平方根,它和方差的作用类似,也是衡量数据离散程度的统计量,由于其单位与原数据单位一致,在实际应用中更便于理解和比较。
【答案】:
刻画数据集中趋势的统计量有平均数、中位数、众数。
特点:平均数利用了所有数据的信息,能反映一组数据的平均水平,但易受极端值影响;中位数不受极端值影响,能更好地反映数据的中间水平;众数可以反映一组数据中出现次数最多的特征,可能不止一个,也可能没有。
刻画数据离散程度的统计量有极差、方差、标准差。
特点:极差计算简单,能反映数据的变化范围,但对其他数据的波动情况反映不全面;方差反映了一组数据与其平均数的偏离程度,能更全面地反映数据的离散情况,但计算相对复杂;标准差和方差作用类似,单位与原数据单位一致,便于理解和比较。
查看更多完整答案,请扫码查看


