《2025年一遍过八年级数学上册北师大版》

1 [2024 临沂河东区月考]计算$\sqrt {24}÷\sqrt {3}-\sqrt {3}×\sqrt {6}$的结果为(A)
A.$-\sqrt {2}$
B.$5\sqrt {2}$
C.$2\sqrt {2}$
D.$\sqrt {2}$

答案： A $\sqrt {24}÷\sqrt {3}-\sqrt {3}×\sqrt {6}=\sqrt {24÷3}-\sqrt {3}×\sqrt {3}×\sqrt {2}=\sqrt {8}-3\sqrt {2}=2\sqrt {2}-3\sqrt {2}=-\sqrt {2}$。

2 [2025 西安西光中学月考]计算$\sqrt {3}×(\sqrt {\frac {1}{3}}+\sqrt {3})$的结果是(B)
A. 2
B. 4
C.$\sqrt {6}$
D.$1+\sqrt {3}$

答案： B $\sqrt {3}×(\sqrt {\frac {1}{3}}+\sqrt {3})=\sqrt {3×\frac {1}{3}}+\sqrt {3×3}=1+3=4$。

3 [2024 楚雄州二模]估计$\sqrt {2}×2\sqrt {3}-\sqrt {6}$的值应在(C)
A. -2 和 -3 之间
B. 1 和 2 之间
C. 2 和 3 之间
D. 7 和 8 之间

答案： C $\sqrt {2}×2\sqrt {3}-\sqrt {6}=2\sqrt {6}-\sqrt {6}=\sqrt {6}$，因为$\sqrt {4}＜\sqrt {6}＜\sqrt {9}$，所以$2＜\sqrt {6}＜3$，估计$\sqrt {2}×2\sqrt {3}-\sqrt {6}$的值应在2和3之间。

4 教材例题变式[2025 南昌期末]老师设计了一个“接力游戏”,用合作的方式完成二次根式的混合运算,如图,老师把题目交给一位同学,他完成一步解答后交给第二位同学,依次进行,最后完成计算。规则是每人只能看到前一人传过来的式子。接力中,自己负责的式子出现错误的是(B)

A. 小明和小丽
B. 小丽和小红
C. 小红和小亮
D. 小丽和小亮

答案： B 因为$(\sqrt {12}+\sqrt {\frac {1}{18}})÷\sqrt {3}=\sqrt {12÷3}+\sqrt {\frac {1}{18}÷3}$，所以小明没有出现错误。因为$\sqrt {12÷3}+\sqrt {\frac {1}{18}÷3}=\sqrt {4}+\sqrt {\frac {1}{18}×\frac {1}{3}}=\sqrt {4}+\sqrt {\frac {1}{54}}$，所以小丽出现错误。因为$\sqrt {4}+\sqrt {\frac {1}{6}}=2+\sqrt {\frac {1×6}{6×6}}=2+\frac {\sqrt {6}}{6}$，所以小红出现错误。因为$2+\sqrt {\frac {1}{36}}=2+\frac {1}{6}=2\frac {1}{6}$，所以小亮没有出现错误。

5 [2025 宿州埇桥区期中]$\frac {\sqrt {8}+\sqrt {18}}{\sqrt {2}}-\sqrt {16}=$1。

答案： 1 $\frac {\sqrt {8}+\sqrt {18}}{\sqrt {2}}-\sqrt {16}=\frac {2\sqrt {2}+3\sqrt {2}}{\sqrt {2}}-4=\frac {5\sqrt {2}}{\sqrt {2}}-4=5-4=1$。

6 计算：
(1)[2024 三明期末]$\frac {\sqrt {20}}{\sqrt {5}}-\sqrt {\frac {1}{3}}×\sqrt {12}+\sqrt {27}$；
(2)[2024 重庆江津区期末]$(5+\sqrt {6})(5\sqrt {2}-2\sqrt {3})$；
(3)$\sqrt {12}÷(\frac {\sqrt {3}}{4}+\frac {2\sqrt {3}}{3})$。

答案： 解：
(1)$\frac {\sqrt {20}}{\sqrt {5}}-\sqrt {\frac {1}{3}}×\sqrt {12}+\sqrt {27}$
$=\sqrt {\frac {20}{5}}-\sqrt {\frac {1}{3}×12}+3\sqrt {3}$
$=\sqrt {4}-\sqrt {4}+3\sqrt {3}$
$=3\sqrt {3}$。
(2)$(5+\sqrt {6})(5\sqrt {2}-2\sqrt {3})$
$=(5+\sqrt {6})×\sqrt {2}(5-\sqrt {6})$
$=\sqrt {2}×(25-6)$
$=19\sqrt {2}$。
(3)$\sqrt {12}÷(\frac {\sqrt {3}}{4}+\frac {2\sqrt {3}}{3})=\sqrt {12}÷\frac {11\sqrt {3}}{12}=\sqrt {12}×\frac {12}{11\sqrt {3}}=\frac {24}{11}$。

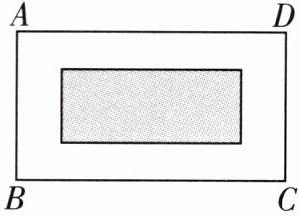
7 [2024 商丘期末]小明家装修,如图,电视背景墙的长 BC 为$\sqrt {27}m$,宽 AB 为$\sqrt {8}m$,中间要镶一个长为$2\sqrt {3}m$,宽为$\sqrt {2}m$的大理石图案(图中阴影部分)。除去大理石图案部分,其他部分贴壁布,求壁布的面积。(结果化为最简二次根式)

解：由题意可得，$\sqrt {27}×\sqrt {8}-2\sqrt {3}×\sqrt {2}=3\sqrt {3}×2\sqrt {2}-2\sqrt {3}×\sqrt {2}=6\sqrt {6}-2\sqrt {6}=$$4\sqrt {6}$$(m^{2})$。
答：壁布的面积为$4\sqrt {6}$$m^{2}$。

答案： 解：由题意可得，$\sqrt {27}×\sqrt {8}-2\sqrt {3}×\sqrt {2}=3\sqrt {3}×2\sqrt {2}-2\sqrt {3}×\sqrt {2}=6\sqrt {6}-2\sqrt {6}=4\sqrt {6}(m^{2})$。
答：壁布的面积为$4\sqrt {6}m^{2}$。

8 [2024 咸阳实验中学月考]先化简,再求值：$(a+\sqrt {3})^{2}-a(a-\sqrt {3})$,其中$a= \sqrt {2}$。

答案： 解：$(a+\sqrt {3})^{2}-a(a-\sqrt {3})$
$=a^{2}+2\sqrt {3}a+3-a^{2}+\sqrt {3}a$
$=3\sqrt {3}a+3$，
当$a=\sqrt {2}$时，原式$=3\sqrt {3}×\sqrt {2}+3=3\sqrt {6}+3$。