《2025年一遍过八年级数学上册北师大版》

1 下列说法错误的是 (A)
A. 平面内两条互相垂直的数轴就构成了平面直角坐标系
B. 平面直角坐标系中两条坐标轴是互相垂直的
C. 坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D. 坐标轴上的点不在任何一个象限内

答案： 1 A 根据平面直角坐标系的定义，在平面内，两条互相垂直且有公共原点的数轴，组成平面直角坐标系，可知 A 选项错误。

2 [2025宁波期末]坐标思想是法国数学家笛卡尔创立的,在平面直角坐标系中,关于点坐标$(-2,4)和(2,-4)$,下列结论正确的是 (D)
A. 横坐标相同
B. 纵坐标相同
C. 所在象限相同
D. 到$y$轴距离相同

答案： 2 D 点$(-2,4)$和$(2,-4)$的横坐标、纵坐标都不相同，点$(-2,4)$在第二象限，点$(2,-4)$在第四象限。点$(-2,4)$和$(2,-4)$到 y 轴的距离相等，均为 2。

3 [教材习题变式][2024滁州期中]在如图所示的平面直角坐标系中描出下列各点：$A(5,-1)$,$B(3,0)$,$C(2,1)$,$D(6,2)$。

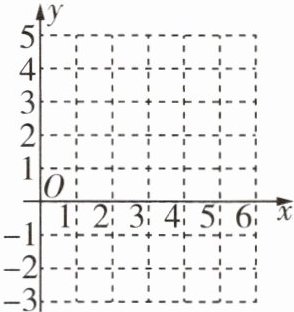
答案：
3 解：如图所示。

4 [新趋势·结论开放][教材随堂练习变式]如图是某中学平面结构示意图(图中每个小正方形的边长均为1个单位)。
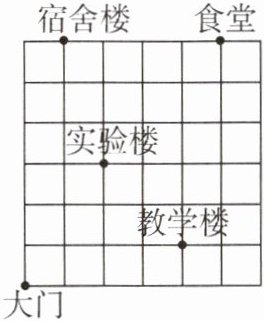
(1)若以大门为坐标原点,以水平向右为$x$轴的正方向,以铅直向上为$y$轴的正方向建立平面直角坐标系,用坐标表示下列位置:实验楼____;教学楼____;食堂____。
(2)请你另建立适当的平面直角坐标系,并写出宿舍楼、实验楼和大门的坐标。

答案：
4 解：
(1)$(2,3)$ $(4,1)$ $(5,6)$
(2)答案不唯一，如：如图，以实验楼为坐标原点，以水平向右为 x 轴的正方向，以铅直向上为 y 轴的正方向建立平面直角坐标系，则宿舍楼的坐标为$(-1,3)$，实验楼的坐标为$(0,0)$，大门的坐标为$(-2,-3)$。

5 [2024茂名期中]数经历了从自然数到有理数、到实数、再到复数的发展过程,数学中把形如$a+bi$($a,b$为实数)的数叫作复数,用$z = a + bi$表示,任何一个复数$z = a + bi在平面直角坐标系中都可以用有序数对z(a,b)$表示。如$z = 1 + 2i表示为z(1,2)$,则$z = 2i - 1$可表示为 (D)
A. $z(2,0)$
B. $z(2,1)$
C. $z(2,-1)$
D. $z(-1,2)$

答案： 5 D

6 [2024河源期末]若点$P在x$轴的下方、$y$轴的左侧,到每条坐标轴的距离都是5,则点$P$的坐标为 (C)
A. $(5,5)$
B. $(-5,5)$
C. $(-5,-5)$
D. $(5,-5)$

答案： 6 C

已知点$P的坐标为(3 - 2a,a - 9)$,且点$P$到两坐标轴的距离相等,则点$P$的坐标为$(-5,-5)$或$(15,-15)$。

答案： 变式 $(-5,-5)$或$(15,-15)$ 因为点 P 到两坐标轴的距离相等，所以$|3-2a|=|a-9|$，所以$3-2a=a-9$或$3-2a=9-a$，解得$a=4$或$a=-6$。当$a=4$时，$3-2a=3-2×4=-5$，$a-9=4-9=-5$。当$a=-6$时，$3-2a=3-2×(-6)=15$，$a-9=-6-9=-15$。所以点 P 的坐标为$(-5,-5)$或$(15,-15)$。

7 [2025中卫沙坡头区期末]课间操时,小华、小军、小刚的位置如图所示,小华对小刚说:“如果我的位置用$(0,0)$表示,小军的位置用$(2,1)$表示,那么你的位置则用$(4,3)$表示。”

答案： 7 $(4,3)$

8 [教材习题变式]如图,在平面直角坐标系中,已知四边形$ABCD$。
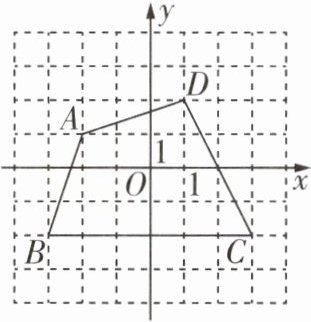
(1)写出点$A,B,C,D$的坐标;$A(-2,1)$，$B(-3,-2)$，$C(3,-2)$，$D(1,2)$
(2)求四边形$ABCD$的面积。$16$

答案： 8 解：
(1)$A(-2,1)$，$B(-3,-2)$，$C(3,-2)$，$D(1,2)$。
(2)$S_{四边形 ABCD}=3×3+2×\frac{1}{2}×1×3+\frac{1}{2}×2×4=16$。