《2025年一遍过八年级数学上册北师大版》

5 [教材习题变式[2023丽水中考]我市“共富工坊”问海借力,某公司产品销售量得到大幅提升。为促进生产,公司提供了两种付给员工月报酬的方案,如图,员工可以任选一种方案与公司签订合同。看图解答下列问题:
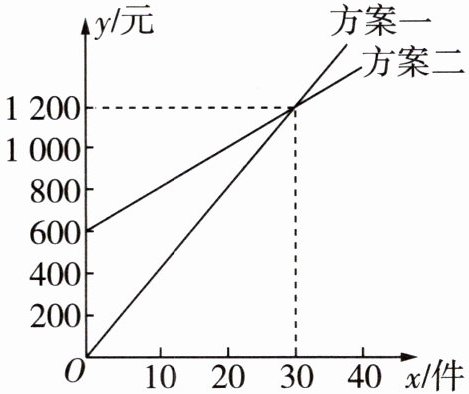
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;30件
(2)求方案二y关于x的函数表达式;y=20x+600
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案。若生产件数不足30件，应选择方案二；若生产件数为30件，两种方案都可以；若生产件数超过30件，应选择方案一

答案： 解：（1）员工生产30件产品时，两种方案付给的报酬一样多。
观察题中图象，可知方案一与方案二对应的函数图象交于点(30,1200)，所以员工生产30件产品时，两种方案付给的报酬一样多。
（2）设方案二对应的函数表达式为y=kx+b，
将(0,600)，(30,1200)代入表达式，得
b=600，30k+b=1200，解得k=20，
即方案二y关于x的函数表达式为y=20x+600。
（3）若生产件数不足30件，应选择方案二；
若生产件数为30件，两种方案都可以；
若生产件数超过30件，应选择方案一。

6 [教材例题变式甲、乙两辆汽车先后从A地出发到B地,甲车出发1h后,乙车才出发,如图所示的$l_{1}和l_{2}$表示甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系。
(1)哪条线表示乙车离出发地的距离y与乙车行驶时间x之间的关系?l₂
(2)甲、乙两车的速度分别是多少?甲车速度为60km/h，乙车速度为90km/h。
(3)试分别确定甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的函数关系式。甲车：y=60x+60；乙车：y=90x。
(4)乙车能在1.5h内追上甲车吗?若能,说明理由;若不能,求乙车行驶几小时才能追上甲车。不能，乙车行驶2小时才能追上甲车

答案： 解：（1）甲车先出发，乙车出发时甲车已经行驶一段距离，结合题中图象，可知l₂表示乙车离出发地的距离y与乙车行驶时间x之间的关系。
（2）甲车的速度为(180-60)÷2=60（km/h），
乙车的速度为90÷1=90（km/h）。
（3）设甲车离出发地的距离y与乙车行驶时间x之间的函数关系式为y=k₁x+b₁（k₁≠0），乙车离出发地的距离y与乙车行驶时间x之间的函数关系式为y=k₂x（k₂≠0），
将(0,60)代入y=k₁x+b₁，得b₁=60，
将(2,180)代入y=k₁x+60，得2k₁+60=180，解得k₁=60，
所以甲车离出发地的距离y与乙车行驶时间x之间的函数关系式为y=60x+60。
将(1,90)代入y=k₂x，得k₂=90，
所以乙车离出发地的距离y与乙车行驶时间x之间的函数关系式为y=90x。
（4）设乙车行驶a h可以追上甲车，
由题意，得90a=60+60a，解得a=2。
因为1.5＜2，
所以乙车不能在1.5h内追上甲车，且乙车行驶2h才能追上甲车。

你能应用一次函数解决哪些问题?

答案： 【解析】：一次函数在实际生活和数学学习中有广泛的应用。在实际生活方面，可用于解决行程问题，比如已知速度和初始距离，通过一次函数来描述物体运动过程中距离与时间的关系；在销售问题中，可根据成本、售价和销售量建立一次函数模型，来分析利润与销售量之间的关系；在工程问题里，能依据工作效率和工作时间建立一次函数，计算工作量等。在数学学习中，可用于解决函数图象与性质相关问题，比如根据一次函数的表达式画出图象，分析其增减性、截距等；还能用于解决方程组和不等式问题，将一次函数与方程、不等式联系起来，通过函数图象求解方程的解和不等式的解集。
【答案】：可解决行程问题、销售问题、工程问题等实际问题，以及函数图象与性质、方程组和不等式等数学问题。