《2025年一遍过八年级数学上册北师大版》

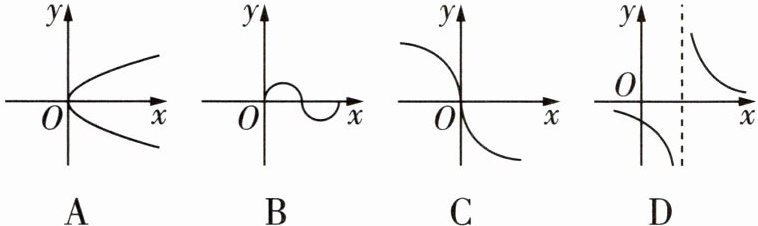
1 [2025郑州二七区期末]下列选项中,y不是x的函数的是(A)

答案： A

2 [2025锦州期中]若$y= (m-2)x^{|m-1|}$为正比例函数,则m的值为(0)
A. 0
B. 1
C. 2
D. 0或2

答案： 根据题意，得$|m - 1| = 1$，且$m - 2 \neq 0$，解得$m = 0$或$m = 2$（舍去）。
易错分析
解答本题时，易忽略正比例函数$y = kx$中$k \neq 0$这一限制条件，只考虑正比例函数中$|m - 1| = 1$，从而得到$m = 0$或$m = 2$。

3 [2024淮南大通区期末]拖拉机开始工作时,油箱中有油24升,如果每小时耗油4升,那么油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象为(D)

答案： D
易错分析
本题的易错之处是不考虑自变量在实际问题中的取值范围。本题容易出现这样的错解：由题意可得，油箱中的余油量$y$与工作时间$x$之间的函数关系式为$y = 24 - 4x$，直接认为自变量的取值范围是所有实数，忽视变量$x$，$y$在实际问题中的含义而选B。在实际问题中列出函数关系式，其自变量的取值范围除了使函数表达式本身有意义外，还要使实际问题有意义。

4 一个水池有水$60m^{3}$,现要将水池中的水排出,如果排水管每小时排出的水量为$3m^{3}$。
(1)写出水池中剩余水量$Q(m^{3})$与排水时间t(h)之间的函数关系式；
(2)画出这个函数图象。

答案：
解：（1）由题意得$Q = 60 - 3t(0 \leq t \leq 20)$。
（2）函数图象如图所示。

5 [2024昆明三中期中]若一次函数$y= kx+b(k≠0)$的图象不经过第三象限,则k,b的取值范围是($k ＜ 0$，$b \geq 0$)
A. $k＜0,b≥0$
B. $k＞0,b＞0$
C. $k＜0,b＞0$
D. $k＞0,b＜0$

答案： 因为一次函数$y = kx + b$的图象不经过第三象限，所以直线$y = kx + b$经过第一、二、四象限或第二、四象限，所以$k ＜ 0$，$b \geq 0$。
易错疑难集训
易错分析
本题容易忽略正比例函数是特殊的一次函数而导致错解。因为正比例函数也是一次函数，所以当$k ＜ 0$，$b = 0$时，$y = kx$，其图象不经过第三象限，也符合条件。

6 [2024合肥期末]若一次函数$y= kx+1(k≠0)在-2≤x≤2$的范围内y的最大值比最小值大8,则下列说法正确的是(A)
A. k的值为2或-2
B. y随x的增大而减小
C. k的值为1或-1
D. 在$-2≤x≤2$的范围内,y的最大值为3

答案： A当$x = 2$时，$y = 2k + 1$，当$x = - 2$时，$y = - 2k + 1$。当$k ＞ 0$时，$y$随$x$的增大而增大，则由题意，得$2k + 1 - (- 2k + 1) = 8$，所以$k = 2$，此时在$- 2 \leq x \leq 2$的范围内，$y$的最大值为$2k + 1 = 5$；当$k ＜ 0$时，$y$随$x$的增大而减小，则由题意，得$- 2k + 1 - (2k + 1) = 8$，所以$k = - 2$，此时在$- 2 \leq x \leq 2$的范围内，$y$的最大值为$- 2k + 1 = 5$。

7 如图,直线$y= \frac {4}{3}x+4$与x轴、y轴分别交于点A,B,P为y轴上的一动点,连接AP,若将$\triangle PAB$沿直线AP翻折,使点B恰好落在x轴上的点$B'$处,求符合条件的点P的坐标。

答案：
解：对于$y = \frac{4}{3}x + 4$，令$x = 0$，得$y = 4$，令$y = 0$，得$x = - 3$，所以$A(- 3,0)$，$B(0,4)$，所以$AO = 3$，$BO = 4$，所以$AB = \sqrt{3^{2} + 4^{2}} = 5$。由折叠易知$\triangle PAB \cong \triangle PAB'$，则$PB = PB'$。设$OP = m$。当点$P$在$y$轴正半轴时，如图1，$PB' = PB = 4 - m$，$OB' = AB' - AO = 2$。在$Rt\triangle POB'$中，$PO^{2} + B'O^{2} = B'P^{2}$，即$m^{2} + 2^{2} = (4 - m)^{2}$，解得$m = \frac{3}{2}$，所以点$P$的坐标为$(0,\frac{3}{2})$。当点$P$在$y$轴负半轴时，如图2，$PB' = PB = 4 + m$，$OB' = AB' + AO = 8$。在$Rt\triangle POB'$中，$PO^{2} + B'O^{2} = B'P^{2}$，即$m^{2} + 8^{2} = (4 + m)^{2}$，解得$m = 6$，所以点$P$的坐标为$(0,- 6)$。综上，符合条件的点$P$的坐标为$(0,\frac{3}{2})$或$(0,- 6)$。