《2025年一遍过八年级数学上册北师大版》

1 [2025上海静安区期中]某风景区集体门票的收费标准是25人以内(含25人),每人10元,超过25人的,超过的部分每人5元。当人数超过25人时,请写出此时应收门票费用y(元)与人数x(人)之间的函数关系式:$ y = 5x + 125(x ＞ 25) $。

答案： $ y = 5x + 125(x ＞ 25) $ 当 $ x ＞ 25 $ 时，得 $ y = 10 \times 25 + 5 \times (x - 25) = 5x + 125 $。

2 某校组织学生到距学校6千米的光明科技馆参观,学生王红因故没能乘上学校的校车,于是准备在学校门口改乘出租车去光明科技馆,出租车收费标准如下:

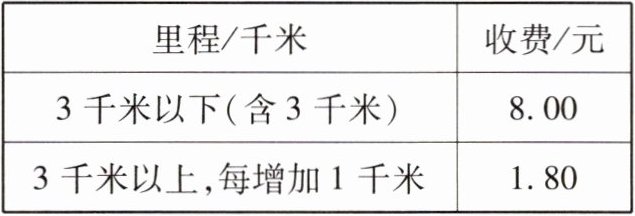
(1)写出出租车的收费y(元)与行驶的里程x(千米)之间的函数关系式;$ y = \begin{cases} 8(0 ＜ x \leq 3) \\ 1.8x + 2.6(x ＞ 3) \end{cases} $
(2)王红同学身上仅有14元钱,则她乘出租车到光明科技馆这些钱够不够用?请说明理由。够，理由：把$ x = 6 $代入$ y = 1.8x + 2.6 $，得$ y = 1.8 × 6 + 2.6 = 13.4 ＜ 14 $

答案： 解：
(1)根据题意，得当 $ 0 ＜ x \leq 3 $ 时，$ y = 8 $，
当 $ x ＞ 3 $ 时，$ y = 1.8(x - 3) + 8 = 1.8x + 2.6 $，
故 $ y $ 与 $ x $ 之间的函数关系式为 $ y = \begin{cases} 8(0 ＜ x \leq 3) \\ 1.8x + 2.6(x ＞ 3) \end{cases} $。
(2)王红同学乘出租车到光明科技馆这些钱够用。理由如下：
把 $ x = 6 $ 代入 $ y = 1.8x + 2.6 $，
得 $ y = 1.8 \times 6 + 2.6 = 13.4 ＜ 14 $，
所以王红乘出租车到光明科技馆这些钱够用。

(1)甲类收费标准每月应缴费用$y_{1}$(元)与通话时间x(min)之间的关系式为$ y_1 = 0.2x + 19 $;乙类收费标准每月应缴费用$y_{2}$(元)与通话时间x(min)之间的关系式为$ y_2 = 0.3x $。
(2)若该电信公司的某位手机用户每月平均通话时间为300min,则该手机用户应选择哪类收费标准比较划算?甲类
(3)当每月平均通话时间为多长时,按甲、乙两类收费标准所缴费用相等?190min

答案： 解：
(1)$ y_1 = 0.2x + 19 $ $ y_2 = 0.3x $
(2)当 $ x = 300 $ 时，$ y_1 = 0.2 \times 300 + 19 = 79 $，$ y_2 = 0.3 \times 300 = 90 $，
因为 $ y_1 ＜ y_2 $，所以该手机用户应选择甲类收费标准比较划算。
(3)由题意，得 $ 0.2x + 19 = 0.3x $，解得 $ x = 190 $，
所以当每月平均通话时间为 $ 190 $ min 时，按甲、乙两类收费标准所缴费用相等。

4 教材随堂练习变式[2025西安曲江二中期中]某市为了鼓励居民节约用电,采用分段计费的方法按月计算用户的电费,每月用电量不超过210kW·h时,按0.55元/(kW·h)计费;每月用电量超过210kW·h时,其中的210kW·h仍按0.55元/(kW·h)计费,超过的部分按0.6元/(kW·h)计费,设用户每月用电量为xkW·h,应交电费y元。
(1)求当x＞210时,y与x的函数关系式。
(2)小林家12月份交纳电费145.5元,小林家这个月的用电量为多少?

答案： 解：
(1)当 $ x ＞ 210 $ 时，$ y $ 与 $ x $ 的函数关系式是 $ y = 0.55 \times 210 + (x - 210) \times 0.6 = 0.6x - 10.5 $，
即当 $ x ＞ 210 $ 时，$ y $ 与 $ x $ 的函数关系式是 $ y = 0.6x - 10.5 $。
(2)当 $ x = 210 $ 时，应交电费 $ 210 \times 0.55 = 115.5 $（元），
因为 $ 115.5 ＜ 145.5 $，所以小林家 12 月份用电量超过 $ 210 $ kW·h，
解方程 $ 145.5 = 0.6x - 10.5 $，得 $ x = 260 $，
所以小林家 12 月份的用电量为 $ 260 $ kW·h。

设计计费规则时要注意什么?

答案： 【解析】：设计计费规则时，首先要确保规则的合理性，要充分考虑成本、市场需求、竞争对手的情况等因素，使价格既能覆盖成本又具有市场竞争力。其次，规则需具备清晰性，要让用户能够容易理解计费的方式和标准，避免产生歧义或误解，减少不必要的纠纷。再者，公平性也很重要，对于不同的用户群体和使用情况，要做到公平对待，不能存在不合理的歧视。另外，还要有灵活性，能够根据市场变化、业务发展等情况进行适时调整。最后，要符合法律法规的要求，不能违反相关的价格政策和监管规定。
【答案】：合理性、清晰性、公平性、灵活性、符合法律法规要求