《2025年一遍过八年级数学上册北师大版》

11 [2025南京玄武区期末]若一次函数$y= kx+b$(k,b是常数,$k≠0$)的图象经过一、二、四象限,则点$(k,b)$在 (B)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： B 因为一次函数$y = kx + b$（$k$，$b$是常数，$k \neq 0$）的图象经过一、二、四象限，所以$k ＜ 0$，$b ＞ 0$，所以点$(k,b)$在第二象限。

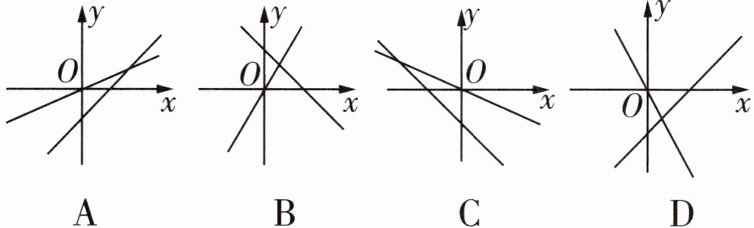
12 [2023陕西中考]在同一平面直角坐标系中,函数$y= ax和y= x+a$(a为常数,$a＜0$)的图象可能是 (D)

答案： D 因为$a ＜ 0$，所以函数$y = ax$的图象经过第二、四象限且过原点，函数$y = x + a$的图象经过第一、三、四象限。

13 [2024乌兰察布集宁区抽测]将直线$y= 2x+1$向上平移2个单位,相当于 (B)
A.向左平移2个单位
B.向左平移1个单位
C.向右平移2个单位
D.向右平移1个单位

答案： B 将直线$y = 2x + 1$向上平移2个单位后，得到新直线的表达式为$y = 2x + 1 + 2$，即$y = 2x + 3$。由于$y = 2x + 3 = 2(x + 1) + 1$，所以将直线$y = 2x + 1$向左平移1个单位即可得到直线$y = 2x + 3$。（上加下减函数值，左加右减自变量）

14 [2024保定期末]在同一平面直角坐标系中,给出下列函数的图象:①$y= x+1$;②$y= 2x+1$;③$y= 2x-1$;④$y= -2x+1$。以下说法不正确的是 (C)
A.②和③的图象互相平行
B.②的图象可由③的图象平移得到
C.①和④的图象关于$y$轴对称
D.③和④的图象关于$x$轴对称

答案： C 由题意，得$y = 2x + 1$与$y = 2x - 1$中的$k$相等，所以②和③的图象互相平行，所以②的图象可由③的图象平移得到，故A项，B项正确；因为$y = 2x - 1 = - ( - 2x + 1)$，所以③和④的图象关于$x$轴对称，故D项正确。

1 在平面直角坐标系中,将正比例函数$y= -2x$的图象向右平移3个单位得到一次函数$y= kx+b(k≠0)$的图象,则该一次函数的表达式为 (B)
A.$y= -2x+3$
B.$y= -2x+6$
C.$y= -2x-3$
D.$y= -2x-6$

答案： B 正比例函数$y = - 2x$的图象向右平移3个单位得到一次函数的表达式为$y = - 2(x - 3)$，即$y = - 2x + 6$。

在平面直角坐标系中,将一次函数$y=x+m$(m为常数)的图象向上平移2个单位后恰好经过原点,若点$A(-1,n)$在一次函数$y=x+m$的图象上,则$n$的值为 (C)
A.1
B.-2
C.-3
D.-4

答案： C 通解 因为将一次函数$y = x + m$（$m$为常数）的图象向上平移2个单位后得到$y = x + m + 2$的图象，且$y = x + m + 2$的图象经过原点，所以$m + 2 = 0$，所以$m = - 2$，又因为点$A( - 1,n)$在一次函数$y = x + m$的图象上，所以$n = - 1 + m = - 1 - 2 = - 3$。
优解 一次函数$y = x + m$（$m$为常数）的图象与$y$轴交于点$(0,m)$，向上平移2个单位后恰好经过原点，所以$m + 2 = 0$，所以$m = - 2$，所以$y = x - 2$，又因为点$A( - 1,n)$在一次函数$y = x - 2$的图象上，所以$n = - 1 - 2 = - 3$。

15 [易错题直线$y= kx+b经过点A(-2,0)$,与$y轴交于点B$,若$\triangle ABO$(O为坐标原点)的面积为2,则$b$的值为±2。

答案： ±2 直线$y = kx + b$经过点$A( - 2,0)$，与$y$轴的交点$B$的坐标是$(0,b)$，由题意得$\frac{1}{2}×2×|b| = 2$，所以$b = ±2$。

16 [新趋势·结论开放如图,直线$y= -\frac {3}{2}x+3与x$轴、$y轴分别交于点A,B$,点$P(m,1)在\triangle AOB$的内部(不含边界),则$m$的值可能是____1。(写出一个即可)

答案： （答案不唯一）1 当$y = 1$时，$- \frac{3}{2}x + 3 = 1$，解得$x = \frac{4}{3}$，所以$0 ＜ m ＜ \frac{4}{3}$。

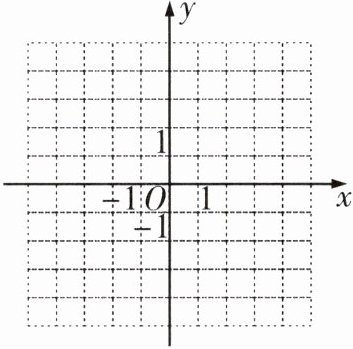
17 [一题多解已知直线$y= kx+2-k$(其中$k≠0$),当$k$取不同数值时,可得不同直线。
(1)①当$k= 1$时,直线$l_{1}$对应的函数表达式为____,请在图中画出直线$l_{1}$。
②当$k= 2$时,直线$l_{2}$对应的函数表达式为____,请在图中画出直线$l_{2}$。
③观察①②的直线,猜想:直线$y= kx+2-k$必经过点(____,____)。
(2)试说明(1)③中你的猜想。

答案：
解：（1）①$y = x + 1$
直线$l_1$如图所示。
②$y = 2x$
直线$l_2$如图所示。

③1 2
（2）通解 把$x = 1$，$y = 2$代入$y = kx + 2 - k$，得左边$= 2$，右边$= k + 2 - k = 2$，左边$=$右边，所以直线$y = kx + 2 - k$必经过点$(1,2)$。
另解 $y = kx + 2 - k = k(x - 1) + 2$，图象过定点，即说明与$k$的取值无关，因此令$x - 1 = 0$，得$x = 1$，所以$y = 2$，所以直线$y = kx + 2 - k$必经过点$(1,2)$。

在平面直角坐标系中,直线$y= -x+m$(m为常数)与$x轴交于点A$,将该直线沿$x$轴向左平移6个单位后,与$x轴交于点A'$。若点$A'与A关于原点O$对称,则$m$的值为 (3)
A.-3
B.3
C.-6
D.6

答案： B 因为直线$y = - x + m$（$m$为常数）与$x$轴交于点$A$，所以$A(m,0)$，将点$A$沿$x$轴向左平移6个单位后，得到点$A'$，所以$A'(m - 6,0)$。因为点$A'$与$A$关于原点$O$对称，所以$m - 6 + m = 0$，解得$m = 3$。

已知一次函数$y= kx+b$的图象与$y= 4x$的图象平行,且图象经过点$(2,5)$,则$b$的值为-3。

答案： - 3 因为直线$y = kx + b$与直线$y = 4x$平行，所以$k = 4$。因为一次函数$y = 4x + b$的图象过点$(2,5)$，所以$5 = 8 + b$，所以$b = - 3$。