《2025年一遍过八年级数学上册北师大版》

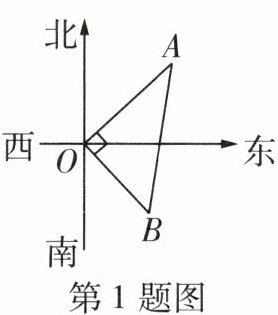
1 [2025洛阳期末]如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为 (40m)

A.45m
B.40m
C.50m
D.56m

答案： B 由题意可知，$∠AOB = 90^{\circ}$，因为$OA = 32m$，$OB = 24m$，由勾股定理，得$AB = 40m$。

2 新趋势·传统文化[2025郑州四十七中期末]《醉翁亭记》中写道:……“射者中……”,其中“射”指投壶,宴饮时的一种游戏。如图,现有一圆柱形投壶内部底面直径是5cm,内壁高12cm,若箭长18cm,则箭在投壶外面部分的长度不可能是 (A)

A.4.5cm
B.5cm
C.5.5cm
D.6cm

答案： A
归纳总结
立体图形中可放入物体最大长度的求法
(1)圆柱体：构建由底面直径、高及物体长度为三边的直角三角形，利用勾股定理求解。
(2)长方体或正方体：首先利用勾股定理求出底面对角顶点连线的长度，再构建由底面对角顶点连线、高及物体长度为三边的直角三角形，利用勾股定理求解。
勾股定理的应用

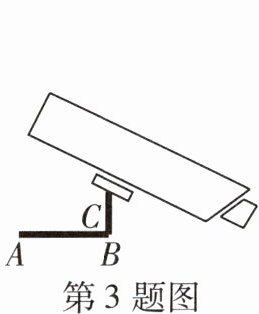
3 [2025南京秦淮区期末]如图,南京地铁公安监控区域的警示图标中,摄像头的支架由水平、竖直方向的AB,BC两段构成,若BC段长度为8cm,点A,C之间的距离比AB段长2cm,则AB段的长度为______cm。

答案：
15 如图，连接$AC$，设$AB = xcm$，则$AC = (x + 2)cm$，因为$∠ABC = 90^{\circ}$，$BC = 8cm$，所以$AB^{2} + BC^{2} = AC^{2}$，所以$x^{2} + 8^{2} = (x + 2)^{2}$，所以$x = 15$，所以$AB = 15cm$。

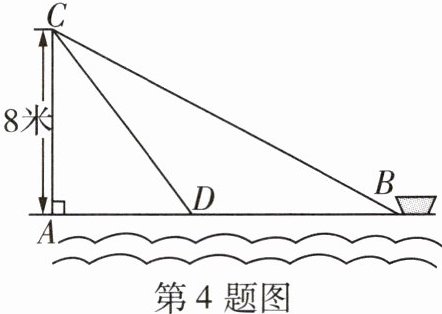
4 [2025重庆黔江区期末]如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了9米。
定理的应用

答案： 9 在$Rt△ABC$中，$∠CAB = 90^{\circ}$，$BC = 17$米，$AC = 8$米，由勾股定理，得$AB = 15$米，在$Rt△ADC$中，$CD = 10$米，由勾股定理，得$AD = 6$米，所以$BD = AB - AD = 15 - 6 = 9$（米），即船向岸边移动了9米。

5 [2025威海期中]公路旁有一块山地正在开发,现有C处需要爆破。已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示。为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明。

答案：
解：公路$AB$段需要暂时封锁。理由如下：
如图，过点$C$作$CD⊥AB$于点$D$。
因为$CA⊥CB$，所以$∠ACB = 90^{\circ}$。
在$Rt△ABC$中，$∠ACB = 90^{\circ}$，$BC = 400$米，$AC = 300$米，
由勾股定理，得$AB^{2} = AC^{2} + BC^{2} = 300^{2} + 400^{2} = 500^{2}$，
所以$AB = 500$米。
因为$S_{△ABC} = \frac{1}{2}AB·CD = \frac{1}{2}BC·AC$，
所以$CD = \frac{BC·AC}{AB} = \frac{400×300}{500} = 240$（米）。
因为$240 ＜ 250$，
所以公路$AB$段需要暂时封锁。

6 [2025佛山南海区月考]如图1、图2分别是某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑竿DE、箱长BC、拉杆AB的长度都相等,即DE= BC= AB= 60cm,点B,F在线段AC上,点C在DE上,支杆DF= 30cm。若EC= 24cm时,B,D相距48cm,连接BD,试判定BD与DE的位置关系,并说明理由。

解：BD⊥DE。理由如下：
在△BDC中，BD = 48cm，BC = 60cm，CD = 60 - 24 = 36(cm)，
因为BC² = 60² = 3600，CD² + BD² = 36² + 48² = 3600，
所以BC² = CD² + BD²，
所以△BDC是直角三角形，∠BDC = 90°，
所以BD⊥DC，即BD⊥DE。

答案： 解：$BD⊥DE$。理由如下：
在$△BDC$中，$BD = 48cm$，$BC = 60cm$，$CD = 60 - 24 = 36(cm)$，
因为$BC^{2} = 60^{2} = 3600$，$CD^{2} + BD^{2} = 36^{2} + 48^{2} = 3600$，
所以$BC^{2} = CD^{2} + BD^{2}$，
所以$△BDC$是直角三角形，$∠BDC = 90^{\circ}$，
所以$BD⊥DC$，即$BD⊥DE$。